Polyèdre isoédrique

En géométrie, un polytope de dimension 3 (un polyèdre) ou plus est dit isoédrique lorsque ses faces sont identiques. Plus précisément, toutes les faces ne doivent pas être simplement isométriques, mais doivent être transitives, c'est-à-dire qu'elles doivent se trouver dans la même orbite de symétrie. En d'autres termes, pour toutes les faces A et B, il doit y avoir une symétrie de l'ensemble du solide par rotations et réflexions qui envoie A sur B. Par exemple, les polyèdres isoédriques convexes fournissent des dés équitables.
Les polyèdres isoédriques sont appelés isoèdres. Ils peuvent être décrits par la configuration des faces. Un isoèdre à sommets réguliers est également transitive pour les arêtes (isotoxale) et est dite dualement quasirégulière. Un isoèdre a un nombre pair de faces.
Un polyèdre isoédrique a un polyèdre dual qui est isogonal, c'est-à-dire à sommets transitifs. Les solides de Catalan, les bipyramides et les trapézoèdres sont tous isoédriques. Ce sont les duaux des solides d'Archimède isogonaux, des prismes et des antiprismes, respectivement. Les solides de Platon, qui sont soit auto-duaux, soit doubles avec un autre solide de Platon, sont isogonaux, isotoxaux et isoédriques. Un polyèdre isoédrique et isogonal est dit noble (en).
Tous les isozonoèdres[1] ne sont pas isoèdres[2]. Exemple : un icosaèdre rhombique est un isozonoèdre non isoèdrique[3].
Exemples
[modifier | modifier le code]| Convexe | Concave | ||
|---|---|---|---|
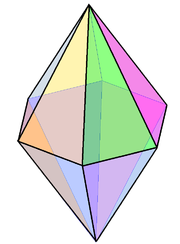 La bipyramide hexagonale, V4.4.6 est un exemple non régulier de polyèdre isoédrique. |
 Le pavage du Caire, V3.3.4.3.4 |
 Le nid d'abeilles dodécaédrique rhombique est un exemple de nid d'abeilles isoédrique (et isochore) remplissant l'espace. |
 Carrelage carré topologique. |
Classes d'isoèdres par symétrie
[modifier | modifier le code]| Faces | config. des faces | Classe | Nom | Symmétrie | Ordre | Convexe | Coplanaire | Non convexe |
|---|---|---|---|---|---|---|---|---|
| 4 | V33 | Platonique | tétraèdre tétraèdre équiface disphénoïde rhombique |
Td, [3,3], (*332) D2d, [2+,2], (2*) D2, [2,2]+, (222) |
24 4 4 4 |
 
|
||
| 6 | V34 | Platonique | cube Trapézoèdre trigonal Trapézoèdre trigonal asymétrique |
Oh, [4,3], (*432) D3d, [2+,6] (2*3) D3 [2,3]+, (223) |
48 12 12 6 |
 
|
||
| 8 | V43 | Platonique | octaère bipyramide carré bipyramide rhombique scalénoère carré |
Oh, [4,3], (*432) D4h,[2,4],(*224) D2h,[2,2],(*222) D2d,[2+,4],(2*2) |
48 16 8 8 |
    
|
||
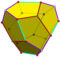
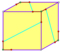
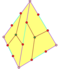
| 12 | V35 | Platonique | dodécaère régulier pyritoère tétartoide |
Ih, [5,3], (*532) Th, [3+,4], (3*2) T, [3,3]+, (*332) |
120 24 12 |
|
|
 
|
| 20 | V53 | Platonique | isocaère régulier | Ih, [5,3], (*532) | 120 | |||
| 12 | V3.62 | Catalan | triakitétraèdre | Td, [3,3], (*332) | 24 |  
|
||
| 12 | V(3.4)2 | Catalan | dodécaèdre rhombique dodécaère trapézoidal |
Oh, [4,3], (*432) Td, [3,3], (*332) |
48 24 |
  
|
 
| |
| 24 | V3.82 | Catalan | triakioctaèdre | Oh, [4,3], (*432) | 48 |  
| ||
| 24 | V4.62 | Catalan | tétrakihexaèdre | Oh, [4,3], (*432) | 48 |  
|
 
|
 
|
| 24 | V3.43 | Catalan | icositétraèdre trapézoïdal | Oh, [4,3], (*432) | 48 |  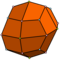
|
  
|
|
| 48 | V4.6.8 | Catalan | hexakioctaèdre | Oh, [4,3], (*432) | 48 |   
|
 
| |
| 24 | V34.4 | Catalan | icositétraèdre pentagonal | O, [4,3]+, (432) | 24 | |||
| 30 | V(3.5)2 | Catalan | triacontaèdre rhombique | Ih, [5,3], (*532) | 120 | |||
| 60 | V3.102 | Catalan | triaki-icosaèdre | Ih, [5,3], (*532) | 120 |    
| ||
| 60 | V5.62 | Catalan | pentakidodécaèdre | Ih, [5,3], (*532) | 120 |     
| ||
| 60 | V3.4.5.4 | Catalan | hexacontaèdre trapézoïdal | Ih, [5,3], (*532) | 120 | |||
| 120 | V4.6.10 | Catalan | hexaki-icosaèdre | Ih, [5,3], (*532) | 120 |   
|
  
| |
| 60 | V34.5 | Catalan | hexacontaèdre pentagonal | I, [5,3]+, (532) | 60 | |||
| 2n | V33.n | Polaire | antidiamant antidiamant asymétrique |
Dnd, [2+,2n], (2*n) Dn, [2,n]+, (22n) |
4n 2n |
  
|
||
| 2n 4n |
V42.n V42.2n V42.2n |
Polaire | bipyramide n-régulière 2n-bipyramide isotoxal 2n-scalénoère |
Dnh, [2,n], (*22n) Dnh, [2,n], (*22n) Dnd, [2+,2n], (2*n) |
4n |   
|
   
|
Termes connexes
[modifier | modifier le code]Une figure est isochore est un n-polytope (n > 3) ou un nid d'abeilles dont les cellules sont congruentes et transitives les unes avec les autres. En 4 dimensions, les polytopes isochores ont été dénombrés jusqu'à 20 cellules[4].
Une figure isotopiques est un polytope à n dimensions ou un nid d'abeilles, avec ses facettes ((n−1)- faces) congruentes et transitives. Le dual d'un isotope est un polytope isogonal.
Références
[modifier | modifier le code]- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Isohedral figure » (voir la liste des auteurs).
- ↑ (en) Weisstein, « Isozonohedron », mathworld.wolfram.com (consulté le )
- ↑ (en) Weisstein, « Isohedron », mathworld.wolfram.com (consulté le )
- ↑ (en) Weisstein, « Rhombic Icosahedron », mathworld.wolfram.com (consulté le )
- ↑ « Four Dimensional Dice Up To Twenty Sides », sur polytope.net (consulté le ).
Liens externes
[modifier | modifier le code]- (en) Eric W. Weisstein, « Isohèdre », sur MathWorld
- (en) Eric W. Weisstein, « Pavage isohédrique », sur MathWorld
- isohedra 25 classes d'isoèdres de nombre d'arêtes fini
- Dice Design at The Dice Lab
- Robert Ferréol, « Polyèdre semi-régulier de deuxième espèce », sur Encyclopédie des formes mathématiques remarquables