Théorème de Descartes (géométrie)
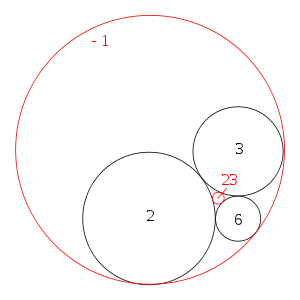
En géométrie, le théorème de Descartes, découvert par René Descartes, établit une relation entre quatre cercles tangents entre eux. Il peut être utilisé pour construire les cercles tangents à trois cercles donnés tangents deux à deux.
Histoire
[modifier | modifier le code]Les problèmes géométriques concernant des cercles tangents sont très anciens. En Grèce antique, trois siècles avant Jésus-Christ, Apollonius de Perga a consacré un livre entier à ce sujet ; malheureusement ce livre, Les Contacts, a disparu. La construction d'un cercle tangent à trois cercles donnés (le plus difficile des problèmes qui figurait dans ce livre) est souvent appelé Problème d'Apollonius. Regiomontanus en a donné une solution algébrique au XVe siècle mais ne croyait pas possible l'existence d'une solution géométrique, François Viète en a proposé la restauration à Adrien Romain, qui en a donné une solution bâtie sur des intersections d'hyperboles. Cette joute est l'occasion pour Viète de montrer la supériorité de son algèbre nouvelle par la publication de Apollonius Gallus[1]. La grande finesse de Viète s'y montre à plein et Michel Chasles découvrira dans cet ouvrage les prémices de l'inversion plane.
René Descartes parle brièvement du problème en 1643, en considérant contrairement à ces prédécesseurs le cas de cercles mutuellement tangents, dans une lettre adressée à la princesse Élisabeth de Bohême à qui il avait soumis le problème[2],[3]. Il a fourni essentiellement la même solution que celle donnée dans la formule ci-dessous, c'est pourquoi son nom a été donné au théorème.
Philip Beecroft, un mathématicien amateur, découvre en 1842 que les configurations de quatre cercles mutuellement tangents apparaissent en paires duales ayant les mêmes points de contact et en déduit une démonstration de la relation de Descartes[4].
Émile Lemoine donne une solution géométrique du problème, minimale dans son système de mesure des constructions.
Frederick Soddy redécouvre la formule en 1936, d'où le nom de formule de Soddy-Descartes donné parfois à cette formule[5]. Les cercles solutions de l'équation sont appelés cercles de Soddy. Ils sont parfois connus sous le nom de kissing circles, peut-être parce que Soddy a choisi d'éditer sa version du théorème sous forme de poésie intitulée The Kiss precise, qui a été imprimé dans Nature le . Soddy a également étendu le théorème aux sphères. Une solution géométrique est détaillée ici[6].
Définition de la courbure
[modifier | modifier le code]Le théorème de Descartes s'énonce simplement en utilisant la courbure des cercles. La courbure d'un cercle est définie par , où r est son rayon. Plus le cercle est grand, plus sa courbure est petite, et vice versa.
Le signe plus dans s'utilise pour un cercle qui est tangent extérieurement aux autres cercles, comme les trois cercles noirs dans la figure ci-dessus. Dans le cas d'un cercle tangent intérieurement, comme le grand cercle rouge dans la figure, on utilise le signe moins.
Le théorème de Descartes
[modifier | modifier le code]Si quatre cercles tangents entre eux ont pour courbure (pour i = 1…4), le théorème de Descartes énonce[5],[4],[7],[8]:
Une démonstration rapide datant de 2022 utilise le fait que le tétraèdre formé par les centres des quatre cercles a un volume donné par le déterminant de Cayley-Menger égal à 0[9].
Cercles de Soddy
[modifier | modifier le code]L'équation (1), vue comme une équation du second degré en , permet d’obtenir la courbure des cercles tangents à trois cercles donnés tangents deux à deux :
Le signe ± indique qu'il existe deux cercles solutions : ce sont les cercles de Soddy ; les deux courbures de ces cercles sont reliés par ; on en déduit que si quatre de ces cinq courbures sont entières, la cinquième l'est aussi.


Cas particulier
[modifier | modifier le code]Si l'un des trois cercles est remplacé par une droite, la courbure (par exemple) est nulle[11]. Ainsi l'équation (2), nous donne :
- ce qui s'écrit aussi : .
Le théorème de Descartes ne s'applique pas lorsque plus d'un cercle est remplacé par une droite.
Le théorème ne s'applique pas non plus lorsque plus d'un cercle est tangent intérieurement, par exemple dans le cas de trois cercles imbriqués tangents en un point.
Théorème complexe de Descartes
[modifier | modifier le code]Afin de définir un cercle complètement, il faut connaitre non seulement son rayon (ou sa courbure), mais aussi son centre. Une relation similaire à celle de Descartes mais faisant aussi intervenir les centres (sous forme complexe ) des quatre cercles mutuellement tangents n'a été découverte qu'en 2001. Elle est connue maintenant sous le nom de théorème complexe de Descartes[12].
Quatre cercles de courbures et de centres d'affixes (pour i = 1…4) sont reliés par la relation :
Une fois trouvée via la relation (2), on peut calculer en réécrivant la relation (4) sous une forme semblable à celle de la relation (2). Il y aura en général de nouveau deux solutions pour , correspondant aux deux solutions pour .
Démonstration par Beecroft de la relation de Descartes, et configuration associée.
[modifier | modifier le code]-
Configuration de Beecroft.
-
Vue des quatre cercles tangents en noir, des quatre cercles tangents grisés, et des trois cercles orthogonaux blancs.
Étant donné trois cercles mutuellement tangents extérieurement de centres , et le cercle minimum qui les englobe, de centre non tracé sur la figure, on note le point de contact de avec (), et le point de contact de avec . On note le cercle passant par , son centre, et le cercle passant par .
On a alors les résultats démontrés par Beecroft, complétés par Soland, suivants[5],[4],[7],[13] :
1) Les cercles sont mutuellement tangents, est le point de contact de avec , et le point de contact de avec .
est le cercle inscrit dans le triangle , le cercle inscrit dans le triangle , le cercle exinscrit associé à dans le triangle , et le cercle inscrit dans le triangle .
On note le rayon algébrique de , sa courbure algébrique, le rayon algébrique de , et sa courbure algébrique.
2) Les huit courbures vérifient les relations de Descartes : et .
3) On a l'égalité et les courbures des sont reliées à celle des par les relations .
4) Si on pose, pour , , les huit courbures sont paramétrées par :
.
La relation de Descartes s'écrit alors : .
5) Géométriquement, le nombre est la courbure du cercle passant par les points de contact cocycliques pour .
Les trois cercles , deux à deux orthogonaux, déterminent la configuration des huit cercles et .

6) Sur la sphère d'équation , on marque les six points d'intersection avec les axes formant un octaèdre régulier.
Les trois grands cercles orthogonaux deux à deux intersections avec les plans de coordonnées sont notés , et les cercles circonscrits aux faces de l'octaèdre sont :
circonscrit à , circonscrit à , circonscrit à , circonscrit à . Les quatre cercles sont mutuellement tangents, ainsi que les quatre .
Alors, par projection stéréographique sur un plan tangent à la sphère de pôle le point antipodal du point de contact du plan avec la sphère, on obtient quatre cercles , quatre cercles et trois cercles du type de la configuration de départ, et on obtient ainsi toutes les configurations possibles.
Notes et références
[modifier | modifier le code]- Anne Boyé, L'Apollonius gallus et le problème des trois cercles comme défense et illustration de la géométrie synthétique, thèse de doctorat (dir. Jean Dhombres), 1998 [présentation en ligne].
- Dana Mackenzie, « La princesse et le philosophe », Pour la Science, no 556, , p. 70-77.
- Lettre de novembre 1643, sur wikisource.
- (en) Philip Beecroft, « Properties of circles in mutual contact », The Lady's and Gentleman's Diary, vol. 139, , p. 91–96 (lire en ligne)
- « Formule de Soddy - Descartes », sur Mathafou
- (en) David Gisch, Jason M. Ribando, « Apollonius’ Problem : A Study of Solutions and Their Connections », American Journal of Undergraduate Research, (lire en ligne)
- (en) Harold Scott Macdonald Coxeter, Introduction to geometry, New York, Wiley, , p. 13-16
- Jean-Pierre Boudine, L'appel des maths, t. 2, Cassini, p. 245-249
- (en) Alden Bradford, « An even more straightforward proof of Descartes’s circle theorem », ArXiv, (lire en ligne)
- Géry Huvent, Sangaku. Le mystère des énigmes géométriques japonaises, Paris, Dunod, 2008, page 60.
- (en) Frank M. Jackson, « Soddyian Triangles », Forum Geometricorum, vol. 13, , p. 1–6 (ISSN 1534-1178, lire en ligne)
- (en) Jeffrey C. Lagarias, Colin L. Mallows, Allan R. Wilks, « Beyond the Descartes Circle Theorem », arXiv, (lire en ligne)
- Christoph Soland, « Le théorème de Descartes et les sangakus »,
Voir aussi
[modifier | modifier le code]Articles connexes
[modifier | modifier le code]Liens externes
[modifier | modifier le code]- (en) Soddy Circles and David Eppstein's Centers: What Are They? sur cut-the-knot : applet java interactive montrant quatre cercles tangents





















































































