Función multivalorada

Este diagrama representa unha función multivalorada ou multifunción: a cada elemento de X facemos corresponder unha parte de Y; así ao elemento 3 de X correspóndelle a parte de Y formada polos dous puntos b e c.

En matemáticas, unha función multivalorada (tamén chamada correspondencia^[1] ou simplemente multifunción) é calquera relación binaria ^[2], chamada impropiamente función porque non é funcional: a cada elemento dun conxunto asocia, non como moito un elemento senón que pode asociar cero, un ou varios elementos dun segundo conxunto. No entanto, podemos ver unha multifunción como unha función clásica tomando os seus valores do conxunto de partes do segundo conxunto^[3]. Pola contra, se a imaxe de cada punto é un singleton, dicimos que a correspondencia é un a un.

Un exemplo sinxelo dunha función multivalorada é a función inversa dunha aplicación non inxectiva: en calquera punto da súa imaxe facemos corresponder a imaxe inversa formada a partir dos antecedentes deste punto.

As funcións multivaloradas aparecen na análise complexa onde podemos considerar ramas das mesmas (ver abaixo ramas e valores principais), é dicir, restricións a estas relacións que as fan funcións e que nos permiten calcular determinadas integrais reais mediante o teorema do residuo como se ilustra a continuación; no entanto, o seu uso é difícil e foi substituído pola consideración máis abstracta de funcións (univaloradas) en superficies de Riemann.

Exemplos

A raíz cadrada

• Nos números reais, para cada elemento positivo x, a relación ${\displaystyle y^{2}=x}$ coincide con dous elementos ${\displaystyle |y|}$ e ${\displaystyle -|y|}$ con ${\displaystyle |y|^{2}=x}$. Adoitamos restrinxirnos ao valor positivo ${\displaystyle |y|}$ para así termos a función raíz cadrada.

• En complexos, ao definir un elemento z do plano complexo ${\displaystyle \mathbb {C} }$ por ${\displaystyle z=|z|\mathrm {e} ^{{\rm {i}}\theta }}$ con ${\displaystyle \theta }$ o argumento de z, as raíces cadradas de z son os números ${\displaystyle w_{k}}$ (${\displaystyle k\in \mathbb {Z} }$) dados por:

${\displaystyle w_{k}={\sqrt {|z|}}\mathrm {e} ^{{\rm {i}}\theta /2}\mathrm {e} ^{{\rm {i}}\pi k}}$

e temos un valor da raíz cadrada por cada valor enteiro que asignemos a k (1, 2, 3 ...).

Comprobamos de feito que ${\displaystyle w_{k}^{2}=|z|\mathrm {e} ^{{\rm {i}}\theta }\mathrm {e} ^{2{\rm {i}}\pi k}=z}$ xa que ${\displaystyle \mathrm {e} ^{2{\rm {i}}\pi k}=1}$ para calquera número enteiro k.

O logaritmo complexo

Definindo un elemento z do plano complexo como antes, os logaritmos complexos de z son os números ${\displaystyle w_{k}}$ (${\displaystyle k\in \mathbb {Z} }$) dado por:

${\displaystyle w_{k}=\ln |z|+{\rm {i}}\theta +2{\rm {i}}\pi k}$

e igual que antes temos un valor por cada enteiro asignado a k.

Comprobamos de feito que ${\displaystyle \exp(w_{k})=|z|\mathrm {e} ^{{\rm {i}}\theta }\mathrm {e} ^{2{\rm {i}}\pi k}=z}$ xa que, como antes, ${\displaystyle \mathrm {e} ^{2{\rm {i}}\pi k}=1}$ para calquera número enteiro k .

As inversas das funcións trigonométricas

• As funcións trigonométricas inversas son multivaloradas porque as funcións trigonométricas son periódicas. Temos

${\displaystyle \tan \left({\tfrac {\pi }{4}}\right)=\tan \left({\tfrac {5\pi }{4}}\right)=\tan \left({\tfrac {-3\pi }{4}}\right)=\tan \left({\tfrac {(2n+1)\pi }{4}}\right)=\cdots =1.}$

Como consecuencia, ${\displaystyle \arctan {(1)}}$ está intuitivamente relacionado con varios valores: π/4, 5π/4, −3π/4, etc.

Podemos tratar a ${\displaystyle \arctan {(x)}}$ como unha función de valor único restrinxindo o dominio de ${\displaystyle \tan {(x)}}$ a ${\displaystyle -\pi /2<x<\pi /2}$, un dominio sobre o que ${\displaystyle \tan {(x)}}$ aumenta monótonamente. Así, o intervalo de ${\displaystyle \arctan {(x)}}$ pasa a ser ${\displaystyle -\pi /2<y<\pi /2}$. Estes valores dun dominio restrinxido chámanse valores principais.

Definicións

Multifunción

Sexan ${\displaystyle X}$ e ${\displaystyle Y}$ dous conxuntos. Unha multifunción ${\displaystyle F:X\multimap Y}$ é unha aplicación de ${\displaystyle X}$ no conxunto ${\displaystyle {\mathcal {P}}(Y)}$ de partes de ${\displaystyle Y}$.

A aplicación que a unha multifunción ${\displaystyle F:X\multimap Y}$, asocia a relación binaria " ${\displaystyle y\in F(x)}$ ", é unha bixección entre as multifuncións de ${\displaystyle X}$ en ${\displaystyle Y}$ e as relacións entre ${\displaystyle X}$ e ${\displaystyle Y}$. É por iso que chamamos gráfica de ${\displaystyle F}$ á gráfica da relación binaria asociada, é dicir, o conxunto

${\displaystyle {\mathcal {G}}(F):=\{(x,y)\in X\times Y\mid y\in F(x)\}}$

(e non gráfica da función ${\displaystyle F}$, que é unha parte de ${\displaystyle X\times {\mathcal {P}}(Y)}$ ).

Dominio, imaxe, selección

Do mesmo xeito, imaxe dunha parte ${\displaystyle P\subset X}$ e imaxe inversa dunha parte ${\displaystyle Q\subset Y}$ mediante unha multifunción ${\displaystyle F:X\multimap Y}$ defínense como a imaxe e a imaxe inversa pola relación binaria asociada:

${\displaystyle {\begin{aligned}F(P)&:=&\{y\in Y\mid \exists x\in P\quad y\in F(x)\}&=&\bigcup _{x\in P}F(x)\\F^{-1}(Q)&:=&\{x\in X\mid \exists y\in Q\quad y\in F(x)\}&=&\{x\in X\mid F(x)\cap Q\neq \varnothing \}.\end{aligned}}}$

En particular, chamamos dominio, ou conxunto de definición^[2],e imaxe, ou conxunto de valores (ou conxunto de imaxes) ^[2], de ${\displaystyle F}$ o dominio e a imaxe da relación binaria asociada:

${\displaystyle {\begin{aligned}{\mathcal {D}}(F)&:=&F^{-1}(Y)&=&\{x\in X\mid F(x)\neq \varnothing \}\\{\mathcal {R}}(F)&:=&F(X)&=&\bigcup _{x\in X}F(x).\end{aligned}}}$

Unha selección de ${\displaystyle F}$ é unha función de escolla, é dicir, unha aplicación ${\displaystyle f:{\mathcal {D}}(F)\to Y}$ tal que ${\displaystyle \forall x\in {\mathcal {D}}(F)\quad f(x)\in F(x)}$.

Multifunción inversa

A multifunción inversa ${\displaystyle F^{-1}:Y\multimap X}$ de ${\displaystyle F:X\multimap Y}$ é a súa relación binaria inversa, definida por ${\displaystyle x\in F^{-1}(y)\Leftrightarrow y\in F(x)}$ .

O dominio e a imaxe de ${\displaystyle F^{-1}}$ son polo tanto respectivamente a imaxe e o dominio de ${\displaystyle F}$.

Algunhas multifuncións especiais

• Sexan ${\displaystyle X}$ e ${\displaystyle Y}$ espazos topolóxicos metrizábeis e sexa ${\displaystyle F:X\multimap Y}$ unha multifunción. Dicimos que ${\displaystyle F}$ é:
  • pechada no punto ${\displaystyle x\in X}$ se ${\displaystyle y\in F(x)}$ sempre que ${\displaystyle (x_{k},y_{k})\in {\mathcal {G}}(F)}$ converxe a ${\displaystyle (x,y)}$;
  • pechada se a súa gráfica é un pechado do espazo produto ${\displaystyle X\times Y}$ (o que equivale a dicir que ${\displaystyle F}$ está pechada en cada punto de ${\displaystyle X}$).
• Se ${\displaystyle X}$ e ${\displaystyle Y}$ son espazos vectoriais reais, dicimos que unha multifunción ${\displaystyle F:X\multimap Y}$ é:
  • convexa se a súa gráfica é convexa ;
  • un proceso convexo se a súa gráfica é un cono convexo puntiagudo.
• Se ${\displaystyle (X,\langle \cdot ,\cdot \rangle )}$ é un espazo pre-Hilbert, dicimos que unha multifunción ${\displaystyle F:X\multimap X}$ é monótona se ${\displaystyle \forall (x,y)\in {\mathcal {G}}(F)\quad \forall (x',y')\in {\mathcal {G}}(F)\quad \langle y-y',x-x'\rangle \geqslant 0}$.

Ramas e valores principais

Para a raíz cadrada complexa e o logaritmo complexo, chamamos rama a unha restrición no argumento ${\displaystyle \theta }$ do valor correspondente. Máis explicitamente, unha rama para a raíz cadrada vén dada por:

${\displaystyle {\sqrt {z}}={\sqrt {|z|}}\mathrm {e} ^{{\rm {i}}\theta /2},\quad (\theta \in [\theta _{0},\theta _{0}+2\pi [)}$

con ${\displaystyle \theta _{0}}$ calquera ángulo que caracterice a determinación. Esta sería a rama principal, que sería asignar o valor cero á fórmula xeral vista arriba ${\displaystyle w_{k}={\sqrt {|z|}}\mathrm {e} ^{{\rm {i}}\theta /2}\mathrm {e} ^{{\rm {i}}\pi k}}$.

Do mesmo xeito, unha rama para o logaritmo complexo vén dada por:

${\displaystyle \log {z}=\ln {|z|}+{\rm {i}}\theta ,\quad (\theta \in ]\theta _{0},\theta _{0}+2\pi ])}$

A restrición do argumento ao intervalo semiaberto ]–π, π] chámase rama principal do logaritmo.

Teña en conta que, ata unha rama, a función de raíz cadrada complexa e o logaritmo complexo son funcións holomorfas en todo o plano complexo agás a semirecta que comeza desde a orixe e cun ángulo ${\displaystyle \theta _{0}}$ en relación ao eixo x. No caso da rama principal, ambas as funcións son holomorfas ${\displaystyle \mathbb {C} \backslash ]-\infty ,0]}$. A descontinuidade no eixo real negativo móstrase na figura seguinte.

• Rama principal
• 
  Figure 1: Ilustración da determinación principal do logaritmo complexo.

Superficies de Riemann

Superficie de Riemann asociada á función raíz cadrada.

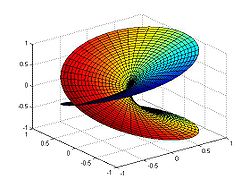
A teoría ineficaz de funcións multivaloradas para funcións de variábeis complexas é substituída nas matemáticas modernas polo concepto máis abstracto dunha función (univalorada) definida nunha superficie de Riemann.

Este punto de vista consiste en considerar o dominio de definición dunha función multivalorada como un obxecto máis elaborado que o plano complexo: unha variedade complexa de dimensión 1.

Notas

1. Aubin & Frankowska 2009, p. 33.
2. Dany-Jack Mercier (2012). Acquisition des fondamentaux pour les concours 1. Publibook. p. 104. .
3. Aubin & Frankowska 2009.

Véxase tamén

Wikimedia Commons ten máis contidos multimedia na categoría:  Función multivalorada

Bibliografía

• Jean-Pierre Aubin; Hélène Frankowska (1990, Birkhäuser). Set-Valued Analysis. Springer. 
• Jean-Pierre Aubin; Arrigo Cellina (1984). Differential Inclusions. Berlin: Springer Grund. math. Wiss. 
• Stanisław Migórski; Anna Ochal; Mircea Sofonea (2012). Nonlinear Inclusions and Hemivariational Inequalities. Springer. 
• Murray R. Spiegel (1973). Variables complexes (PDF). New York/Montréal/Paris: MacGraw-Hill / Ediscience. ISBN 2-7042-0020-3. Arquivado dende o orixinal (PDF) o 14 de febreiro de 2017. Consultado o 04 de marzo de 2025. 

Outros artigos

• Rama (matemáticas)
• Valor principal
• Análise complexa
• Superficie de Riemann
• Teorema do residuo