Tetración

Coloreado do dominio da tetración definida como función holomorfa ${\displaystyle {}^{z}e}$, co ton representando o argumento e o brillo representando o módulo.

En matemáticas, a tetración (ou hiper-4) é o seguinte hiperoperador despois da potenciación, e é definida como unha potenciación iterada. A palabra provén de tetra (catro) e ción (de iteración). A tetración é usada para a notación dos números moi grandes.

Introdución

Para entender a tetración hai que entender a relación xerárquica que teñen a suma, a multiplicación e a exponenciación: as multiplicacións poden entenderse como sumas repetidas, a potenciación como multiplicacións repetidas e a tetración como potenciacións repetidas. Todas estas operacións repetidas forman unha xerarquía de "hiperoperacións" que consisten en repetir certo número de veces a operación do nivel inferior. Aquí preséntanse exemplos dos primeiros catro operadores, coa tetración como o primeiro hiperoperador.

1. Adición

   ${\displaystyle a+n=a+\!\underbrace {1+1+...+1} _{n}}$

   a unidade 1 añadida a "a" n veces.

2. Multiplicación

   ${\displaystyle a\times n=\underbrace {a+a+\cdots +a} _{n}}$

   a sumado n veces.

3. Potenciación

   ${\displaystyle a^{n}=\underbrace {a\times a\times \cdots \times a} _{n}}$

   a multiplicado n veces.

4. Tetración

   ${\displaystyle {^{n}a}=\underbrace {a^{a^{\cdot ^{\cdot ^{a}}}}} _{n}}$

n copias de a combinadas por exponenciación, de dereita a esquerda.

Teña en conta que os expoñentes aniñados interprétanse convencionalmente de arriba abaixo: ${\displaystyle a^{b^{c}}}$ significa ${\displaystyle a^{\left(b^{c}\right)}}$ e non ${\displaystyle \left(a^{b}\right)^{c}.}$

Na tetración cada operación é definida mediante a iteración da operación previa (a seguinte operación na sucesión é a pentación). A peculiaridade da tetración entre estas operacións é que para as tres primeiras (adición, multiplicación e potenciación) poden ser xeneralizadas para valores complexos de n, mentres que para a tetración, tal xeneralización regular non está actualmente establecida; a tetración non é considerada unha función elemental.

A adición ${\displaystyle (a+n)}$ é a operación máis básica, a multiplicación ${\displaystyle (an)}$ é tamén unha operación primaria, aínda que para os números naturais pode ser pensada como a adición encadeada que implica n números a, e a potenciación ${\displaystyle (a^{n})}$ pode ser pensada como unha multiplicación encadeada que implica n números a.

Análogamente, a tetración ${\displaystyle ({}^{n}a)}$ pode ser pensada como unha potencia encadeada con n expoñentes a. O parámetro a chámase base, mentres que o parámetro n, altura (que é enteiro na primeira aproximación, pero pódese xeneralizar a alturas fraccionais, reais e complexas)

Definición

Para calquera número real positivo ${\displaystyle a>0}$ e un número enteiro non negativo ${\displaystyle n\geq 0}$, defínese ${\displaystyle \,\!{^{n}a}}$ como:

${\displaystyle {^{n}a}:={\begin{cases}1&{\text{se }}n=0\\a^{\left[^{(n-1)}a\right]}&{\text{se }}n>0\end{cases}}}$

Exemplos de potencias iteradas contra bases iteradas/potenciación

Como se pode ver da definición, ao avaliar a tetración, esta exprésase como unha "torre de expoñentes", a potenciación realízase no nivel máis alto primeiro para que esta sexa irreducible. Dito doutro modo:^[1]

${\displaystyle \,\!^{4}2=2^{(2^{(2^{2})})}=2^{(2^{4})}=2^{16}=65536}$

Nótese que a potenciación non é asociativa, así que avaliar a expresión noutra orde proporcionará unha resposta diferente ademais de incorrecta:

${\displaystyle \,\!\ ^{4}2=((2^{2})^{2})^{2}=({4^{2}})^{2}=16^{2}=256}$

Simplificaríase a 2^(2^(4-1))=2^(2^3)=2^8=256, que é unha dobre exponencial.

Polo tanto, as torres exponenciais deben ser avaliadas de arriba abaixo (ou de dereita a esquerda), xa que a tetración é unha función exponencial iterada.

Propiedades

A tetración ten varias propiedades que son similares á potenciación, así como propiedades que son específicas da operación e que se perden ou gañan coa potenciación. Debido a que a potenciación non é conmutativa, as regras do produto e da potencia non teñen un análogo coa tetración; as afirmacións ${\textstyle {}^{a}\left({}^{b}x\right)=\left({}^{ab}x\right)}$ e ${\textstyle {}^{a}\left(xy\right)={}^{a}x{}^{a}y}$ non son certas para a maioría dos casos.^[2]

Pola contra, a tetración segue unha propiedade diferente, onde ${\textstyle {}^{a}x=x^{\left({}^{a-1}x\right)}}$. Este feito vese máis claramente usando unha definición recursiva. Desta propiedade séguese que ${\displaystyle \left({}^{b}a\right)^{\left({}^{c}a\right)}=\left({}^{c+1}a\right)^{\left({}^{b-1}a\right)}}$, o que permite intercambiar b e c en determinadas ecuacións. A demostración desta propiedade é a seguinte:

${\displaystyle {\begin{aligned}&\left({}^{b}a\right)^{\left({}^{c}a\right)}\\={}&\left(a^{{}^{b-1}a}\right)^{\left({}^{c}a\right)}\\={}&a^{\left({}^{b-1}a\right)\left({}^{c}a\right)}\\={}&a^{\left({}^{c}a\right)\left({}^{b-1}a\right)}\\={}&\left({}^{c+1}a\right)^{\left({}^{b-1}a\right)}\end{aligned}}}$

Cando un número x e 10 son coprimos, entón pódense computar as últimas m cifras decimais de ${\displaystyle \,\!\ ^{a}x}$ empregando o teorema de Euler, para calquera enteiro m. Isto é certo tamén noutras bases: por exemplo, as últimas m cifras octais de ${\displaystyle \,\!\ ^{a}x}$ pódense calcular cando x e 8 son coprimos.

Xeneralizacións

A tetración pódese xeneralizar de dúas maneiras diferentes; na ecuación ${\displaystyle ^{n}a!}$, tanto a base a como a súa altura n pódense xeneralizar empregando a definición e as propiedades da tetración. Aínda que a base e a altura pódense xeneralizar máis alá dos enteiros non negativos a diferentes dominios, incluíndo ${\displaystyle {^{n}0}}$, funcións complexas como ${\displaystyle {}^{n}i}$, e alturas de infinito n, as propiedades máis limitadas da tetración reducen a capacidade de xeneralizala.

Base cero ou complexa

Base cero

A potencia ${\displaystyle 0^{0}}$ non está definida de forma consistente. Polo tanto, as tetracións ${\displaystyle \,{^{n}0}}$ tampouco están claramente definidas pola fórmula dada anteriormente. Pola contra, ${\displaystyle \lim _{x\rightarrow 0}{}^{n}x}$ está ben definida, e existe:

${\displaystyle \lim _{x\rightarrow 0}{}^{n}x={\begin{cases}1,&n{\text{ par}}\\0,&n{\text{ impar}}\end{cases}}}$

Por ende, poderíamos definir consistentemente ${\displaystyle {}^{n}0=\lim _{x\rightarrow 0}{}^{n}x}$. Isto é análogo a definir ${\displaystyle 0^{0}=1}$. Baixo esta xeneralización, ${\displaystyle {}^{0}0=1}$, polo que a regra ${\displaystyle {{0}a}=1}$ da definición orixinal segue vixente.

Bases complejas

Tetración por período

Tetración por escape

Dado que os números complexos pódense elevar a potencias, a tetración pódese aplicar a bases da forma z = a + bi (onde a e b son reais). Por exemplo, en ⁿz con z = i, a tetrización obtense empregando a rama principal do logaritmo natural; utilizando a fórmula de Euler obtemos a relación:

${\displaystyle i^{a+bi}=e^{{\frac {1}{2}}{\pi i}(a+bi)}=e^{-{\frac {1}{2}}{\pi b}}\left(\cos {\frac {\pi a}{2}}+i\sin {\frac {\pi a}{2}}\right)}$

Isto suxire unha definición recursiva para ${\displaystyle {}^{n+1}i=a'+b'i}$ dado calquera ${\displaystyle {}^{n}i=a+bi}$:

${\displaystyle {\begin{aligned}a'&=e^{-{\frac {1}{2}}{\pi b}}\cos {\frac {\pi a}{2}}\\[2pt]b'&=e^{-{\frac {1}{2}}{\pi b}}\sin {\frac {\pi a}{2}}\end{aligned}}}$

Isto permite encontrar os seguintes valores aproximados:

Valores da tetración de bases complexas

${\textstyle {}^{n}i}$	Valor aproximado
${\textstyle {}^{1}i=i}$	i
${\textstyle {}^{2}i=i^{\left({}^{1}i\right)}}$	0.2079
${\textstyle {}^{3}i=i^{\left({}^{2}i\right)}}$	0.9472 + 0.3208i
${\textstyle {}^{4}i=i^{\left({}^{3}i\right)}}$	0.0501 + 0.6021i
${\textstyle {}^{5}i=i^{\left({}^{4}i\right)}}$	0.3872 + 0.0305i
${\textstyle {}^{6}i=i^{\left({}^{5}i\right)}}$	0.7823 + 0.5446i
${\textstyle {}^{7}i=i^{\left({}^{6}i\right)}}$	0.1426 + 0.4005i
${\textstyle {}^{8}i=i^{\left({}^{7}i\right)}}$	0.5198 + 0.1184i
${\textstyle {}^{9}i=i^{\left({}^{8}i\right)}}$	0.5686 + 0.6051i

Xeneralizacións para diferentes alturas

Alturas infinitas

${\displaystyle \textstyle \lim _{n\rightarrow \infty }{}^{n}x}$ da potencial infinitamente iterada converxe para as bases ${\displaystyle \textstyle \left(e^{-1}\right)^{e}\leq x\leq e^{\left(e^{-1}\right)}}$.

A función ${\displaystyle left|{\frac {\mathrm {W} (-\ln {z})}{-\ln {z}}}\ln {z}|}$ no plano complexo, mostrando a función exponencial infinitamente iterada de valor real (curva negra)

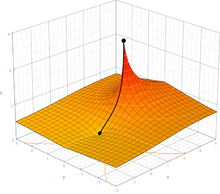
A tetración pódese estender ás alturas infinitas; é dicir, para certos valores de a e n en ${\displaystyle {}^{n}a}$, existe un resultado ben definido para un n infinito. Isto débese a que para bases dentro dun certo intervalo, a tetrización converxe a un valor finito a medida que a altura tende ao infinito. Por exemplo, ${\displaystyle {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{\cdot ^{\cdot ^{}}}}}}$ converxe a 2, e por tanto pódese dicir que é igual a 2. A tendencia a 2 pódese ver avaliando unha pequena torre finita:

${\displaystyle {\begin{aligned}{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1.414}}}}}&\approx {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1.63}}}}\\&\approx {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1.76}}}\\&\approx {\sqrt {2}}^{{\sqrt {2}}^{1.84}}\\&\approx {\sqrt {2}}^{1.89}\\&\approx 1.93\end{aligned}}}$

En xeral, a pontencial infinitamente iterada ${\displaystyle x^{x^{\cdot ^{\cdot ^{\cdot }}}}\!\!}$, definida como o límite de ${\displaystyle {}^{n}x}$ a medida que n crece a infinito, converxe para ${\displaystyle e^{-e}\leq x\leq e^{1/e}}$, aproximadamente o intervalo de 0.066 a 1.44, resultado demostrado por Leonhard Euler. O límite, se existe, é unha solución real positiva da ecuación 1=y = x^y. Así, 1 =x = y^1/y. O límite que define a exponencial infinita de x non existe cando x > e^1/e porque o máximo de y^1/y é e^1/e. O límite tampouco existe cando 0 < x < e^-e. Isto pódese estender aos números complexos z coa definición:

${\displaystyle {}^{infty}z=z^{z^{\cdot ^{\cdot ^{\cdot }}}}={\frac {\mathrm {W} (-\ln {z})}{-\ln {z}}}~,}$

onde ${\displaystyle W}$ representa a función W de Lambert.

Como o límite 1=y = ^∞x (se existe na recta real positiva, é dicir para e^-e ≤ x ≤ e^1/e) debe satisfacer 1=x^y = y vemos que 1=x ↦ y = ^∞x é (a rama inferior de) a función inversa de 1=y ↦ x = y^1/y.

Alturas negativas

Podemos utilizar a regra recursiva da tetración,

${\displaystyle {^{k+1}a}=a^{\left({^{k}a}\right)},}$

para demostrar que ${\displaystyle {}^{-1}a}$:

${\displaystyle ^{k}a=\log _{a}\left(^{k+1}a\right);}$

Substituíndo -1 por k obtense

${\displaystyle {}^{-1}a=\log _{a}\left({}^{0}a\right)=\log _{a}1=0}$.^[1]

Os valores negativos máis pequenos non poden ser ben definidos desta maneira. Substituíndo -2 por k na mesma ecuación obténse

${\displaystyle {}^{-2}a=\log _{a}\left({}^{-1}a\right)=\log _{a}0=-\infty }$

que non está ben definida. Mais, ás veces pódense considerar conxuntos.^[1]

Para ${\displaystyle n=1}$, calquera definición de ${\displaystyle \,\!{^{-1}1}}$ é consistente coa regra porque

${\displaystyle {^{0}1}=1=1^{n}}$ para calquera ${\displaystyle ,\!n={^{-1}1}}$.

Alturas reais

Neste momento non existe unha solución comunmente aceptada para o problema xeral de estender a tetración aos valores reais ou complexos de n. Aínda así, existen múltiples enfoques cara esa cuestión, e a continuación esbózanse diferentes enfoques.

En xeral, o problema é encontrar, para calquera real a > 0, unha función superexponencial ${\displaystyle ,f(x)={}^{x}a}$ sobre reais x > -2 que satisfaga

• ${\displaystyle \,{}^{-1}a=0}$
• ${\displaystyle \,{}^{0}a=1}$
• ${\displaystyle \,{}^{x}a=a^{\left({}^{x-1}a\right)}}$para todo número real ${\displaystyle x>-1.}$^[3]

Notas

1. Müller, M. "Reihenalgebra: What comes beyond exponentiation?" (PDF). Arquivado dende o orixinal (PDF) o 02 de decembro de 2013. Consultado o 2018-12-12. 
2. Meiburg, Alexander (2014). "Extensión analítica de la tetración a través del producto Power-Tower" (PDF). Arquivado dende o orixinal (PDF) o 30 de novembro de 2018. Consultado o 29 de novembro de 2018. 
3. "5+ methods for real analytic tetration". 2010-06-28. Consultado o 2018-12-05. 

Véxase tamén

Bibliografía

• Daniel Geisler, tetration.org
• Ioannis Galidakis, On extending hyper4 to nonintegers (undated, 2006 or earlier) (A simpler, easier to read review of the next reference)
• Ioannis Galidakis, On Extending hyper4 and Knuth's Up-arrow Notation to the Reals (undated, 2006 or earlier).
• Robert Munafo, Extension of the hyper4 function to reals (An informal discussion about extending tetration to the real numbers.)
• Lode Vandevenne, Tetration of the Square Root of Two, (2004). (Attempt to extend tetration to real numbers.)
• Ioannis Galidakis, Mathematics, (Definitive list of references to tetration research. Lots of information on the Lambert W function, Riemann surfaces, and analytic continuation.)
• Weisstein, Eric W. "Power Tower". MathWorld. 
• Joseph MacDonell, Some Critical Points of the Hyperpower Function Arquivado 26 de outubro de 2022 en Wayback Machine..
• Dave L. Renfro, Web pages for infinitely iterated exponentials (Compilation of entries from questions about tetration on sci.math.)
• R. Knobel. "Exponentials Reiterated." American Mathematical Monthly 88, (1981), p. 235–252.
• Takeji Ueda. Extension of tetration to real and complex heights (2021).
• Hans Maurer. "Über die Funktion ${\displaystyle y=x^{[x^{[x(\cdots )]}]}}$ für ganzzahliges Argument (Abundanzen)." Mittheilungen der Mathematische Gesellschaft in Hamburg 4, (1901), p. 33–50. (Reference to usage of ${\displaystyle \ {^{n}a}}$ from Knobel's paper.)
• Ripà, Marco (2011). La strana coda della serie n^n^...^n, Trento, UNI Service. ISBN 978-88-6178-789-6

Outros artigos

• Hiperoperación
• Pentación

Ligazóns externas

• Andrew Robbins' site on tetration
• Daniel Geisler's site on tetration
• Tetration Forum
• tetration at citizendium
• Gottfried Helms' site on tetration