הדרגתיות פילטית
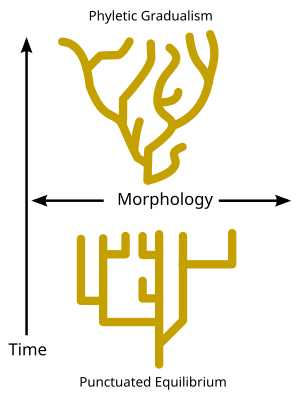
הדרגתיות פילטית (באנגלית: Phyletic gradualism) היא מודל של אבולוציה המשער שרוב היווצרות המינים היא איטית, אחידה והדרגתית.[1] האבולוציה במצב זה קורית בדרך כלל על ידי טרנספורמציה של מין למין חדש (באמצעות תהליך שנקרא אנאגנזה). בתפיסה זו לא קיים קו גבול ברור בין מין קדמון למין צאצא, אלא אם כן מתרחש פיצול. התיאוריה מעומתת עם התאוריה של שיווי משקל מקוטע.
היסטוריה
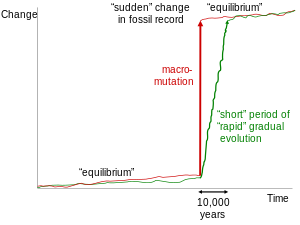
[עריכת קוד מקור | עריכה]המילה phyletic נובעת מהמילה היוונית φυλετικός (בתעתיק ללטינית – phūletikos), שמשמעותה "מוצא" או "צאצא".[2] הדרגתיות פילטית מעומתת עם תאוריית שיווי המשקל המקוטע, המציעה שרוב האבולוציה מתרחשת בפרקים נדירים ומבודדים של אבולוציה מהירה, כאשר מין בודד מתפצל לשני מינים נפרדים, ואחריו יש תקופה ארוכה של אי-שינוי. מודלים אלה מנוגדים למודל האבולוציה במהירות משתנה, שגורסת שמינים שונים מתפתחים בקצב שונה ושאין סיבה להעדיף בתיאוריה את קיומו של קצב שינוי אחד על פני קיומו של אחר.[3][4]
התאוריות אינן סותרות מכיוון שכל מודל תקף בסביבה שונה. למשל, יש בעלי חיים שלא משתנים במשך מאות מיליוני שנים, מכיוון שסביבתם כמעט לא השתנתה ולכן לא פעל עליהם לחץ הברירה הטבעית להשתנות. מינים אלה מכונים "מאובן חי". לעומתם, יש מינים שמשתנים עקב שינוי בתנאי הסביבה, למשל היכחדות הדינוזאורים לפני כ-66 מיליון שנה, היכחדות שפינתה נישה אקולוגית שאפשרה את התפתחות היונקים הקטנים, מהם התפתח האדם.
הביולוג האבולוציוני ריצ'רד דוקינס טוען שהדרגתיות בקצב קבוע אינה קיימת בספרות המקצועית, ולכן המונח משמש רק כאיש קש לתומכי שיווי משקל מקוטע. בספרו השען העיוור, ציין דוקינס שדרווין עצמו לא תמך בתאוריית שיווי המשקל המקוטע, שאותה הציעו אלדריג' וגולד. במהדורה הראשונה של על מוצא המינים, דרווין קבע כי "מינים מסוגים וממחלקות שונים לא השתנו באותו קצב, או באותה מידה. במרבצים העתיקים ביותר מתור השלישון עדיין ניתן למצוא כמה קונכיות חיות בלב שפע צורות נכחדות. . . הלינגולה (Lingula) מתור הסילור שונה אך מעט מהמינים החיים של סוג זה".[5]
לינגולה (Lingula) (אנ') היא בין הברכיופודים הבודדים ששרדו כיום אך ידוע גם ממאובנים בני למעלה מ-500 מיליון שנה. במהדורה החמישית של "מוצא המינים", כתב דרווין כי "התקופות שבהן המינים עברו שינוי, אם כי הן ארוכות בשנים, כנראה היו קצרות בהשוואה לתקופות שבהן הם שומרים על אותה צורה",[6] מה שמהווה מעין פשרה בין תאוריית שיווי המשקל המקוטע ותאוריית הקפיצה, לבין תאוריית ההדרגתיות.
קישורים חיצוניים
[עריכת קוד מקור | עריכה]הערות שוליים
[עריכת קוד מקור | עריכה]- ^ Eldredge, N. and S. J. Gould (1972). "Punctuated equilibria: an alternative to phyletic gradualism" In T.J.M. Schopf, ed., Models in Paleobiology. San Francisco: Freeman Cooper. p. 84.
- ^ φυλετικός phūletikos originates from φυλέτης phūletēs "one of the same tribe," from φυλή phulē, "clan, race, people", derived from φύεσθαι phuesthai, "to descend, to originate."
- ^ Dawkins, Richard. 1996. The Blind Watchmaker. New York: W. W. Norton & Company. מסת"ב 0-393-31570-3
- ^ Futuyma, Douglas. 2005. Evolution. Sunderland MA: Sinauer Associates, pp. 86-89
- ^ Charles Darwin, 1859. On the origin of species London: John Murray. 1st edition, p. 313.
- ^ Charles Darwin, 1869. The Origin of Species London: John Murray. 5th edition, p. 551.