התפלגות היפרגאומטרית שלילית

התפלגות בינומית

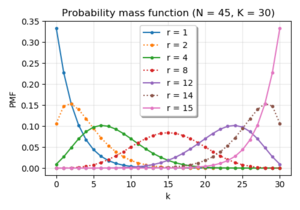
פונקציית ההסתברות
פונקציית ההסתברות המצטברת
מאפיינים
פרמטרים	${\displaystyle N\in \left\{0,1,2,\dots \right\}}$ - מספר כולל של איברים ${\displaystyle K\in \left\{0,1,2,\dots ,N\right\}}$ - מספר כולל של איברים שהם 'הצלחות' ${\displaystyle r\in \left\{0,1,2,\dots ,N-K\right\}}$ - מספר איברים שהם 'כישלונות' כשעוצרים את הבחירות
תומך	${\displaystyle k\in \{0,1,2...,K\}}$
פונקציית הסתברות (pmf)	${\displaystyle {\frac {{{k+r-1} \choose {k}}{{N-r-k} \choose {K-k}}}{N \choose K}}}$
תוחלת	${\displaystyle r{\frac {K}{N-K+1}}}$
שונות	${\displaystyle r{\frac {(N+1)K}{(N-K+1)(N-K+2)}}[1-{\frac {r}{N-K+1}}]}$

בתורת ההסתברות ובסטטיסטיקה, התפלגות היפרגאומטרית שלילית היא התפלגות בדידה המתארת הסתברויות לדגימה ללא החזרה מאוכלוסייה סופית המחולקת לשתי קטגוריות זרות שמכונות באופן שרירותי "הצלחות" ו-"כישלונות". כאשר נערך מדגם מקרי מתוך האוכלוסייה, כמו בהתפלגות ההיפרגאומטרית, כל בחירה אקראית של איבר במדגם מקטינה את האוכלוסייה ומשנה את ההסתברות ל-"הצלחה". בניגוד להתפלגות היפרגאומטרית המתארת את מספר ההצלחות בגודל מדגם קבוע, ההתפלגות ההיפרגאומטרית השלילית, מתארת את ההסתברות לדגימת ${\displaystyle k}$ "הצלחות" עד שנדגמו r "כישלונות".

הגדרה

נתונה קבוצה של ${\displaystyle N}$ איברים, מתוכם ${\displaystyle K}$ מוגדרים כ"הצלחות" והשאר "כישלונות".

בוחרים באופן אקראי, מתוך הקבוצה, איבר, איבר ללא החזרה, עד שמבין האיברים שנבחרו יש ${\displaystyle r}$ כישלונות. מספר ה-"הצלחות" ${\displaystyle k}$ שנבחרו עד אותו הרגע מהווה משתנה מקרי ${\displaystyle X}$ עם ההתפלגות ההיפרגאומטרית השלילית. ניתן לסמן זאת באופן הבא: ${\displaystyle X\sim NHG(N,K,r)}$.^[1]

ההתפלגות ההיפרגאומטרית השלילית היא מקרה פרטי של ההתפלגות הבטא-בינומית^[2] עם פרמטרים שלמים ${\displaystyle \alpha =r}$ ו ${\displaystyle \beta =N-K-r+1}$ ו- ${\displaystyle n=K}$.

בנתונים אלו, כדי לקבל ${\displaystyle X=k}$, חייבות להתרחש במהלך ה-${\displaystyle (k+r-1)}$ הבחירות הראשונות בדיוק ${\displaystyle k}$ בחירות של "הצלחות" (ההסתברות לכך ניתנת לחישוב באמצעות יישום ישיר של ההתפלגות ההיפרגאומטרית ${\displaystyle HG(N,K,k+r-1)}$), ואז הבחירה ה-${\displaystyle k+r}$ חייבת להיות "כישלון" (ההסתברות לכך היא ה-"כישלונות" שעדיין לא נבחרו ${\displaystyle N-K-(r-1)}$ לחלק במספר כל האיברים שעדיין לא נבחרו ${\displaystyle N-(k+r-1)}$ ). לכן, ההסתברות שיש בדיוק ${\displaystyle k}$ "הצלחות" עד ל"כישלון" ה- ${\displaystyle r}$-י כשל היא מכפלה שתי ההסתברויות :

${\displaystyle {\frac {{\binom {K}{k}}{\binom {N-K}{k+r-1-k}}}{\binom {N}{k+r-1}}}\cdot {\frac {N-K-(r-1)}{N-(k+r-1)}}={\frac {{{k+r-1} \choose {k}}{{N-r-k} \choose {K-k}}}{N \choose K}}.}$

לכן, פונקציית ההסתברות (pmf) של משתנה מקרי ${\displaystyle X}$ עם התפלגות היפרגאומטרית השלילית ניתנת על ידי

${\displaystyle f(k;N,K,r)\equiv \Pr(X=k)={\frac {{{k+r-1} \choose {k}}{{N-r-k} \choose {K-k}}}{N \choose K}}\quad {\text{, }}k=0,1,2,\dotsc ,K}$

כאשר

• ${\displaystyle N}$ הוא מספר כלל האיברים,
• ${\displaystyle K}$ הוא מספר כלל האיברים המוגדרים כ"הצלחה",
• ${\displaystyle r}$ הוא מספר האיברים שיבחרו שהם "כישלונות",
• ${\displaystyle k}$ הוא מספר האיברים שיבחרו שהם "הצלחות",
• ${\displaystyle a \choose b}$ הוא מקדם בינומי

התפלגויות קשורות

התפלגות היפרגאומטרית שלילית (כמו ההתפלגות ההיפרגאומטרית) עוסקת בהגרלות ללא החזרה, כך שההסתברות ל"הצלחה" שונה בכל בחירה. לעומת זאת, התפלגות בינומית שלילית (כמו ההתפלגות הבינומית) עוסקת בבחירות עם החזרה, כך שההסתברות להצלחה זהה והניסויים בלתי תלויים. הטבלה הבאה מסכמת את ארבעת ההתפלגויות הקשורות:

	עם תחליפים	אין תחליפים
מספר "הצלחות" מתוך מספר קבוע של בחירות אקראיוח	התפלגות הבינומית	התפלגות היפרגאומטרית
מספר "הצלחות" שמתרחש עד שמתקבל מספר קבוע מראש של "כישלונות"	התפלגות בינומית שלילית	התפלגות היפרגאומטרית שלילית

אם ${\displaystyle X}$ הוא משתנה מקרי בעל התפלגות היפרגאומטרית שלילית, ${\displaystyle X\sim NHG(N,K,r)}$ ו-${\displaystyle Y}$ הוא משתנה מקרי היפרגאומטרי, ${\displaystyle Y\sim HG(N,N-K,k+r)}$ אז מתקיים ${\displaystyle F_{X}(k)=1-F_{Y}(r-1)}$, כאשר ${\displaystyle F_{X},F_{Y}}$ הן פונקציות ההצטברות (cdf) של ${\displaystyle X,Y}$ בהתאמה. באופן שקול ניתן לכתוב, ${\displaystyle \Pr(X\leq k)=\Pr(Y\geq r)}$. ^[1]

לעיתים^[3][4] מגדירים את ההתפלגות ההיפרגאומטרית השלילית כמספר ההגרלות הנדרשות עד לקבלתה"כישלון" ה-${\displaystyle r}$-י. אם נסמן ב- ${\displaystyle Y}$ את המספר הזה אז ברור ש ${\displaystyle Y=X+r}$ כאשר ${\displaystyle X}$ הוא כפי שהוגדר למעלה. מכאן פונקציית ההסתברות (pmf):

${\displaystyle \Pr(Y=y)={\binom {y-1}{r-1}}{\frac {\binom {N-y}{N-K-r}}{\binom {N}{N-K}}}}$

אם נסמן ב-${\displaystyle M}$ את כלל ${\displaystyle N-K}$ האיברים שהם "כישלונות" אז,

${\displaystyle \Pr(Y=y)={\binom {y-1}{r-1}}{\frac {\binom {N-y}{M-r}}{\binom {N}{M}}}}$

התומך של ${\displaystyle Y}$ הוא הקבוצה ${\displaystyle \{r,r+1,\dots ,N-M+r\}}$ ולכן,

${\displaystyle E[Y]=E[X]+r={\frac {r(N+1)}{M+1}}}$, ו- ${\displaystyle {\textrm {Var}}(X)={\textrm {Var}}(Y)}$.

הערות שוליים

1. Negative hypergeometric distribution in Encyclopedia of Math.
2. Johnson, Norman L.; Kemp, Adrienne W.; Kotz, Samuel (2005). Univariate Discrete Distributions. Wiley. ISBN 0-471-27246-9. §6.2.2 (p.253–254)
3. Rohatgi, Vijay K., and AK Md Ehsanes Saleh. An introduction to probability and statistics. John Wiley & Sons, 2015.
4. Khan, RA (1994). A note on the generating function of a negative hypergeometric distribution. Sankhya: The Indian Journal of Statistics B, 56(3), 309-313.