ספקטרוסקופיית רוויה

ספקטרוסקופיית רוויה מאפשרת ניתוח מבנה האטום ברזולוציה גבוהה יותר. באיור העליון נראה האפיון הספקטרלי ללא ספקטרוסקופיית רוויה. שימוש בטכניקה זו מראה שהמלבן מהאיור העליון מורכב למעשה מכמה קווי בליעה (איור תחתון).

בפיזיקה אטומית, ספקטרוסקופיית רוויה (באנגלית: Saturated Spectroscopy)^[1], היא טכניקה למדידת רמות האנרגיה באטום ברזולוציה גבוהה ("המבנה העל דק").

תאורטית, אור מונוכרומטי יכול להבלע כאשר הוא פוגע באטום אם לאור ישנה בדיוק אנרגיה המתאימה למעבר בין רמות האנרגיה באטום, אנרגיית מעבר זו נגזרת מתכונות האטום. בפועל, קיימות הרחבות ספקטרליות שונות כגון הרחבה טבעית, הרחבת לחץ, הרחבת דופלר, המאפשרות בליעה בטווח אנרגיות רחב ומונעות גילוי מדויק של ספקטרום הבליעה. ספקטרוסקופיית רוויה מאפשרת לגלות את טווח האנרגיות בהן האור נבלע ללא אפקט הרחבת דופלר.

משמעות השם ספקטרוסקופיית רוויה היא בחינה של ספקטרום התדרים באטום כאשר החלקיקים מעוררים למצב אנרגיה גבוה ממצב היסוד עד לכך שהמצב המעורר "רווי" בחלקיקים.

טכניקות מקובלות נוספות למציאת רמות האנרגיה ברזולוציה גבוהה מהרחבת דופלר הן ספקטרוסקופיית קיטוב (Polarization Spectroscopy), אשר פותחה על בסיס ספקטרוסקופיית רוויה^[2], ובליעת שני אטומים (Two Photon Absorption).

מלבד מציאת רמות האנרגיה טכניקה זו משמשת לנעילת לייזר לתדר צר^[3].

רקע היסטורי

ספקטרוסקופיה היא תחום מחקר בו נמדד ספקטרום רמות אנרגיה או ספקטרום תדרי קרינה אלקטרומגנטית. במאה ה-19 נעשו התקדמויות משמעותיות בתחום, ותחום זה היווה בסיס לפיתוח מכניקת הקוונטים. הלייזר וקודמו המייזר, פותחו על ידי מדענים שעסקו בספקטרוסקופייה באמצע המאה ה-20, המצאה זו אפשרה מדידה ברזולוציה גבוהה יותר מאי-פעם.^[4].

בשנת 1970 תיאודור האנש (Theodor Wolfgang Hänsch) - זוכה פרס נובל לשנת 2005 לפיזיקה, וקריסטיאן בורדו (Christian Bordé), הציגו לראשונה בנפרד מערכת לקבלת ספקטרום האטום ללא הרחבת דופלר, אשר הייתה מבוססת על עקרון של בחינת הספקטרום כאשר האטומים ברוויה. את השימוש בספקטרוסקופיית רוויה פיתח ארתור שולוב (Arthur L. Schawlow), בשיטת inter-modulated fluorescence, על פיתוח זה בין היתר, זכה בפרס נובל לפיזיקה בשנת 1981, שאותו חלק עם ניקולס בלומברגן וקאי סיגבאן על מחקרם בספקטרוסקופיה^[5].

אפיון המבנה האטומי בעזרת לייזר היה כרוך בקשיים הנובעים מיצירת לייזר עם אורכי גל בטווחים מתאימים לכל אטום. קושי זה בלט בעיקר בתחומי האולטרא סגול, ובתחילה שליטה על תדר הלייזר נעשתה בשיטות כגון שינוי הטמפרטורה והפעלת שדה מגנטי. בשנות ה-70 הוצג לראשונה לייזר רציף בתחום צר של אורכי גל, עם יכולת כיוון גבוהה, דבר אשר גרם לשיפור משמעותי ביכולת אפיון חומרים. במשך השנים הללו אטומים רבים אופיינו במעבדות שונות, ביניהם אטום המימן אשר בעזרתו נקבע בדיוק רב יותר קבוע רידברג ^[6].

לאור ההתקדמות הטכנולוגית בפיתוח לייזרים, ובעיקר דיודות לייזר, המערכת לביצוע ספקטרוסקופיית רוויה נעשתה פשוטה ביותר, וניתנת כיום לסטודנטים כניסוי מעבדה באוניברסיטאות רבות. כמו כן ניתן לקנות ערכה לביצוע ספקטרוסקופייה בחברות שונות העוסקות בתחום^[7].

רקע פיזיקלי

באיור שמאל מתוארות הרמות האלקטרוניות (n=1, n=2, n=3) באיור ימין מתוארת פיצול ברמות האלקטרוניות, פיצולי המבנה הדק והמבנה העל-דק של אטום מימן

אחד המאפיינים הייחודיים של מכניקת הקוונטים, היא העובדה שהערכים המתארים את המערכת (אנרגיה, תנע זוויתי, ספין וכו') הם בדידים ולא רציפים, בניגוד למכניקה הקלאסית. אלקטרונים יכולים לנוע סביב הגרעין אך ורק באורביטלים מוגדרים (קונפיגורציה אלקטרונית), הנמצאים ברמות אנרגיה בדידות אשר מתוארות על ידי מספרים קוונטיים. המשמעות הפרקטית העיקרית לכך שרמות האנרגיה הן בדידות היא שמעבר אלקטרון בין רמות אנרגיה ${\displaystyle E_{1},E_{2}}$ יכול להתאפשר בעזרת קבלת/פליטת אנרגיה ספציפית ${\displaystyle \ E_{2}-E_{1}=h\nu =\hbar \omega }$ כאשר "h" הוא קבוע פלאנק.

אף על-פי שרמות האנרגיה הן בדידות, ישנה תופעה של הרחבה ספקטרלית המרחיבה כל רמת אנרגיה לטווח ערכים. תופעה זו מקשה על מדידת ספקטרום רמות האנרגיה ברזולוציה גבוהה, מכיוון שבליעה של פוטון בתדר ${\displaystyle \nu _{1}}$ אינה מהווה אינדיקציה לכך שהפרש האנרגיות המתאים לתדר הפוטון ${\displaystyle \Delta E=h\nu _{1}}$ הוא באמת הפרש רמות האנרגיה היסודי באטום.

רמות האנרגיה מתחלקות לרמות אלקטרוניות, כאשר כל רמה אלקטרונית מתפצלת למבנה הדק, וכל מבנה דק מתפצל למבנה העל-דק. ספקטרוסקופיית רוויה מאפשרת להבחין במבנה העל-דק באטום.

הרחבות ספקטרליות

אי ודאות מרחיבה כל אחת מרמות האנרגיה (איור שמאל), ולכן ישנו טווח תדרים בהם מתאפשר מעבר (איור ימין)

ערך מורחב – הרחבות ספקטרליות

הרחבה טבעית

כאשר אלקטרון מעורר לרמה אלקטרונית, הוא שוהה בה פרק זמן של עד כמה עשרות ננו-שניות, וחוזר עצמאית לרמה אנרגטית נמוכה יותר.

כיוון שקיימת אי ודאות בזמן חזרת האלקטרון קיימת אי ודאות בציר האנרגיה, כפי שמתואר בעיקרון אי-הוודאות של הייזנברג:

${\displaystyle \Delta E\cdot \Delta t\geq {h \over 2\pi }}$

כאשר ${\displaystyle h}$ הוא קבוע פלאנק, ${\displaystyle \Delta E}$ הוא אי הוודאות באנרגיה, ו - ${\displaystyle \Delta t}$ הוא אי הוודאות בזמן.

הקשר בין אנרגיה לתדירות נתון על ידי: ${\displaystyle E=h\nu }$, ומשתי המשוואות מקבלים: ${\displaystyle \Delta \nu ={\Delta E \over h}\geq {1 \over 2\pi \cdot \Delta t}}$ .

לדוגמה, עבור רובידיום, מעברים בין הפיצולים במבנה העל-דק הם כ- ${\displaystyle \Delta t\approx 27ns}$, והצבה נותנת את גודל ההרחבה הטבעית : ${\displaystyle \Delta \nu _{natural}\approx 6MHz}$.

הרחבת דופלר

איורים א-ג מראים פוטונים בתדרים שונים הפוגעים באטומים עם היטל מהירות זהה בציר התקדמות הפוטון. תנועת האטומים גורמת לפוטונים בתדרים שונים להבלע. באיור ד' רואים פוטונים בתדרים שונים פוגעים באטומים הנעים רנדומלית, ולכן את פרופיל הרחבת דופלר.

הרחבת דופלר מתרחשת עקב תנועתם של האטומים (במידה ולא מקררים אותם למילי-קלווין בודדים). לולא היו האטומים בעלי אנרגיה, מציאת אנרגיית המעבר הייתה אפשרית על ידי לזירת פוטונים בעלי אנרגיות בגדלים שונים, עד למציאת האנרגיה בה הפוטון נבלע (עד כדי הרחבה טבעית). אנרגיית התנועה של האטומים גורמת לבליעת פוטונים בטווח אנרגיות גדול יותר.

בהינתן תא של גז אטומי, ההסתברות שלאטום תהיה מהירות בין ${\displaystyle v}$ ל - ${\displaystyle v+dv}$ מתפלגת על פי התפלגות מקסוול בולצמן :

${\displaystyle P(v)dv={\sqrt {\frac {m}{2\pi k_{B}T}}}e^{-{\frac {mv^{2}}{2k_{B}T}}}dv}$

כאשר ${\displaystyle k_{B}}$ הוא קבוע בולצמן, ${\displaystyle m}$ הוא מסת האטום, ו - ${\displaystyle T}$ הוא הטמפרטורה המוחלטת.

לפי אפקט דופלר הלא יחסותי: ${\displaystyle \omega =\omega _{0}\left(1\pm {\frac {v}{c}}\right)}$, כאשר ${\displaystyle \omega _{0}}$ הוא תדר המעבר בין רמות האנרגיה כאשר האטומים במנוחה (התדר הרצוי).

הצבת ${\displaystyle v}$ בהתפלגות מקסוול בולצמן למהירות, נותנת את התוצאה: ${\displaystyle P(v)dv={\frac {2}{\delta {\pi ^{1/2}}}}e^{-{\frac {4(v-v_{0})^{2}}{\delta ^{2}}}}dv}$

כאשר ${\displaystyle \delta }$ הוא פרמטר רוחב הפס הספקטרלי (linewidth parameter ), ונתון על ידי: ${\displaystyle \delta ={2{\frac {v_{0}}{c}}}{({\frac {2k_{B}T}{m}})}^{1/2}}$

מכאן ניתן למצוא את רוחב חצי המקסימום ${\displaystyle \Delta \nu =\delta {\sqrt {ln(2)}}}$ התלוי במסת האטום, בטמפרטורה, ובתדר המעבר.

לדוגמה, עבור רובידיום בטמפרטורת החדר מתקיים :${\displaystyle \Delta \nu _{doppler}\approx 500MHz}$, לעומת זאת - ${\displaystyle \Delta \nu _{natural}\approx 6MHz}$. הרחבת דופלר היא המגבילה בצורה משמעותית את רוחב הסרט המדיד.

ספקטרוסקופיית רוויה

לשם ההסבר, נתייחס ראשית לאוסף אטומים הנמצאים במצב גזי ונניח שהאטומים נמצאים במנוחה.

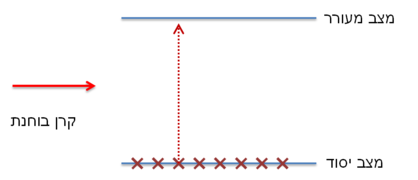
בטמפרטורת החדר אטומים רבים נמצאים ברמת היסוד. כאשר קרן באנרגיית המעבר (הנקראת גם אנרגיית הרזוננס) תפגע בתא האטומים בעוצמה נמוכה, אחוז גבוה מהקרן יבלע, ומספר אלקטרונים מועט יחסית יעלה לרמת אנרגיה גבוהה יותר (איור א'). במידה וקרן באנרגיית הרזוננס תפגע בתא האטומים בעוצמה גבוהה, אלקטרונים רבים יחסית יעברו ממצב היסוד למצב מעורר. תופעה זו נקראת רוויה של המעבר (transition saturated). בשני המקרים מדידת עוצמת האור המתקבלת לאחר מעבר בתא האטומים תהיה נמוכה משמעותית מהעוצמה לפני המעבר בתא עקב הבליעה.

הקרן החלשה נקראת קרן בוחנת (probe beam), והחזקה - קרן שואבת (pump beam). כאשר הקרן הבוחנת והקרן השואבת תפגענה באטומים בו זמנית בתדר הרזוננס (איור ב'), הקרן השואבת תגרום לאלקטרונים רבים מרמת היסוד לעלות רמת אנרגיה, ולכן לקרן הבוחנת יהיו פחות אלקטרונים ברמת היסוד איתם תוכל להיות אינטראקציה. כתוצאה מכך, אחרי המעבר בתא האטומים עוצמת הקרן הבוחנת לא תהיה שונה משמעותית מלפני המעבר.

• 
  איור א - פוטון הפוגע באטום יבלע בהסתברות גבוהה עקב אלקטרונים רבים ברמת היסוד.
• 
  איור ב - קרן שואבת מעלה אלקטרונים רבים למצב מעורר, ולכן הסתברות בליעת פוטון בקרן הבוחנת נמוכה.

במערכת של שתי רמות אנרגיה, העוצמה הנמדדת לאחר מעבר קרן בוחנת דרך תא אטומים תתפלג לפי הרחבת דופלר (איור ימין). הוספת קרן שואבת תגרום לקבלת עוצמה גבוהה במדידת הקרן הבוחנת (איור שמאל).

כעת, נסתכל על אוסף אטומים במצב גזי הנמצאים בתנועה.

בטמפרטורת החדר האטומים בעלי אנרגיה ולכן נמצאים בתנועה. הרחבת דופלר גורמת לבליעה להתרחש לא רק באנרגיית הרזוננס, אלא בספקטרום רחב מאוד של כ - 500MHz סביב אנרגיית המעבר. נבחן שוב את המערכת בה קרן בעוצמה חזקה וקרן בעוצמה חלשה עוברות בו זמנית בתא האטומים (איור ב') עם אנרגיות שונות. באנרגיה נמוכה במעט מאנרגיית הרזוננס, הקרן הבוחנת תיבלע בפגיעה באטום הנע שמאלה (לפי הכיוונים באיור ב'), כך שסכום האנרגיות שלהם מתאים לאנרגיית הרזוננס (עד כדי הרחבה טבעית). אבל, עבור הקרן השואבת האטום שיעורר הוא אטום הנע ימינה. אותה טענה מתקיימת גם עבור אנרגיה גבוהה מאנרגיית הרזוננס.

אם כך, באנרגיות שונות מאנרגיית הרזוננס שתי הקרניים מקיימות אינטראקציה עם אטומים שונים, ולכן נוכחות קרן אחת לא משפיעה על סיכויי הבליעה של הקרן השנייה. לעומת זאת, באנרגיית הרזוננס שתי הקרניים מגיבות עם אותם אטומים - אטומים הנעים במאונך לקרניים, מכיוון שהם לא תורמים לאנרגיה של הפוטונים הפוגעים. כעת הקרן השואבת תכניס את האטומים הללו לרוויה, ומדידת העוצמה של הקרן הבוחנת אחרי המעבר בתא האטומים לא תהיה שונה משמעותית.

ניתן למדל ביתר קלות את הסתברויות הבליעה כאשר ישנו אלקטרון אחד חופשי באטום, ולכן במתכות אלקליות (נתרן, אשלגן, רובידיום, צסיום), אשר קיים אלקטרון אחד ברמת הערכיות האחרונה, מקבלים תוצאות מובנות יותר אינטואיטיבית^[8]. סיבה זו גרמה לכך שהאפיונים הראשונים נעשו באטומים אלו, כמו ניסויי המעבדה הניתנים באוניברסיטאות השונות.

פרופיל הבליעה כפונקציה של אורך הגל. האיור הכחול הוא ללא הקרן השואבת, והאיור האדום הוא עם הקרן השואבת.

באיור משמאל מוצג ספקטרום בליעה אופייני, הגרף הכחול הוא ללא הקרן השואבת, ולכן לא ניתן להבחין בפיצולי המבנה העל-דק. הגרף האדום הוא עם הקרן השואבת, ולכן מתאפשרת רזולוציה ספקטרלית גבוהה יותר. מקובל לחסר בין הגרפים על מנת למדוד ביתר קלות את רוחב המבנה העל-דק, ולהציג תוצאה ברורה יותר^[9].

דגשים בבניית המערכת

• יחסי עוצמות – יש חשיבות רבה לכך שהקרן השואבת תעורר את האטומים במצב היסוד למצב של רוויה של המעבר (transition saturated). העוצמה משתנה כתלות בטמפרטורה וגורמים נוספים, אך באופן כללי הקרן השואבת צריכה להיות חזקה פי 10 בעוצמתה מהקרן הבוחנת.
• תדר הקרניים – גורם קריטי לכך שהניסוי יעבוד הוא שהתדר של הקרן השואבת והקרן הבוחנת יהיה זהה. לשם כך מפצלים את הקרן לשתיים, ואחת מהן מונחתת בדרך כלל בעזרת מנחת אופטי או מפצל קרניים.
• זווית בין הקרניים – הזווית בין הקרניים גם היא משפיעה על כמות האטומים הנפגעים על ידי הקרן השואבת והבוחנת. באופן אידיאלי זווית של 0 מעלות תתן תוצאה טובה ביותר, אך גם זווית של 4-5 מעלות תתן תוצאות טובות.
• דיודת לייזר – יש להשתמש בלייזר בעל רזולוציה ספקטרלית גבוהה מההרחבה הטבעית, לשם כך משתמשים בדרך כלל בדיודת לייזר בעלת רוחב פס של כמה מגה-הרצים בודדים. כמו כן, יציבות התדר תלויה ביציבות הטמפרטורה ויציבות הזרם, לכן רצוי מאוד להשתמש בבקר טמפרטורה ובקר זרם. סריקת התדרים מתבצעת בעזרת מחולל אותות, עם אות משולש, בתדר נמוך.
• אינטרפרומטר פברי-פרו – לשם הבנה טובה יותר של התוצאות המתקבלות, כדאי לפצל את קרן האור שעוברת מודלציה בתדר, ולהעביר אותה דרך אינטרפרומטר פברי-פרו. בצורה כזו ניתן לקבל את ספקטרום הבליעה יחד עם אומדן של המרחקים על-פני הספקטרום.

ראו גם

• רמת אנרגיה
• ספקטרוסקופיה

לקריאה נוספת

• W. Demtröder, Laser Spectroscopy: Basic Concepts and Instrumentation, springer, 2003

קישורים חיצוניים

מדיה וקבצים בנושא ספקטרוסקופיית רוויה בוויקישיתוף

• Saturated Absorption Spectroscopy of Rubidium

הערות שוליים

1. קרוי גם "ספקטרוסקופיית בליעה רוויה" (Saturated Absorption Spectroscopy) או "ספקטרוסקופיית ללא הרחבת דופלר" (Doppler-Free Spectroscopy)
2. http://laser.physics.sunysb.edu/~james/papers/wieman-hansch.1976.pdf
3. Laser Locking with Doppler-free Saturated Absorption Spectroscopy , Paul L. Stubbs, May 12, 2010
4. סיכום זה מבוסס על המאמר שנשא פרופ' ארתור שולוב בטקס קבלת פרס נובל לפיזיקה בשנת 1981.
5. ביוגרפיה של ארתור שולוב, אתר זוכי פרס נובל
6. Precision Measurement of the Rydberg Constant Hänsch, T. W. Department of Physics, Stanford University, 1974
7. בחברות מסחריות כגון Newport ,Thorlabs ,Toptica
8. מצגת מעבדה מתקדמת בספקטרוסקופיית רוויה, אוניברסיטת נוטרדאם, עמוד 2
9. ראו כאן איור להמחשה