צבר מיקרוקנוני
במכניקה הסטטיסטית, צבר מיקרוקנוני הוא צבר המייצג את כלל המצבים האפשריים של מערכת מכנית בעלת אנרגיה כוללת מסוימת.[1] תוך הנחה כי המערכת מבודדת לחלוטין מסביבתה, כלומר אנרגיה או חלקיקים אינם יכולים לצאת או להיכנס מהמערכת או אליה, וכך (על פי חוק שימור האנרגיה) האנרגיה של המערכת נותרת בדיוק כפי שהיא בחלוף הזמן. האנרגיה, ההרכב, הנפח, והצורה של המערכת זהים בכל המצבים האפשריים של המערכת.
המשתנים המאקרוסקופיים הנשלטים של צבר מיקרוקנוני הם הגדלים המשפיעים על טבעם של המצבים הפנימיים (המיקרו־מצבים) של המערכת, כמו המספר הכולל של חלקיקים במערכת (מסומן בN), נפח המערכת (מסומן ב־V) והאנרגיה הכוללת את המערכת (מסומן ב־E). צבר זה נקרא לפעמים צבר NVE, שכן כל אחד משלושת הגדלים הללו הוא קבוע של צבר.
בפשטות, ההרכב המיקרוקנוני מתקבל על ידי התהליך הבא: מניחים קצאת הסתברות שווה לכל מיקרו־מצב בעל אנרגיה הנמצאת בטווח צר סביב E. כל שאר המיקרומצבים מקבלים הסתברות של אפס. מאחר שההסתברויות חייבת להסתכם ל־1, ההסתברות למיקרומצב יחד, P, שווה להופכי של מספר מיקרומצבים, W, השייכים לטווח האנרגיה, , כעת נצמצם את רוחב טווח האנרגיה עד שהוא צר באופן אינפיניטסימלי, אך עדיין מרוכז ב־E. בגבול של תהליך זה מתקבל הצבר המיקרוקנוני.[1]
יישומים
[עריכת קוד מקור | עריכה]הצבר המיקרוקנוני נחשב לפעמים לחלוקה הבסיסית של התרמודינמיקה הסטטיסטית, שכן צורתו יכולה להיות מוצדקת על ידי הנחות יסודיות כגון עקרון האדישות: הצבר המיקרו־קנוני מתאר את המצבים האפשריים של מערכת מכנית מבודדת אשר האנרגיה שלה ידועה בדיוק, אך ללא מידע נוסף על מצבה הפנימי. כמו כן, בחלק מהמערכות המיוחדות ההתפתחות בזמן היא ארוגודית, ובמקרה זה, הצבר המיקרו־קנוני זהה להרכב הצבר־זמן אשר מתחיל עם מצב יחיד של אנרגיה E (צבר־זמן הוא הצבר המתאר את כלל המצבים העתידיים שהתפתחו ממצב התחלתי יחיד).
בפועל, הצבר המיקרו־קנוני אינו תואם לתמונה מציאותית. בכל מערכת פיזית אמיתית יש לכל הפחות חוסר ודאות כלשהו באנרגיה, בשל גורמים בלתי מבוקרים בהכנת המערכת. מלבד הקושי למצוא תַּקְבִּיל ניסיוני, ישנו קושי ליישם במדויק חישובים המספקים את הדרישה של אנרגיה קבועה שכן היא מונעת נתוח נפרד של חלקים עצמאיים מבחינה לוגית של המערכת. יתר על כן, ישנה עמימות בהגדרת גדלים כמו אנטרופיה וטמפרטורה בצבר המיקרוקנוני.[1]
מערכות הנמצאות בשיווי משקל תרמודינמי עם הסביבתם יש חוסר ודאות באנרגיה, לכן הן אינן מתוארות על ידי צבר מיקרוקנוני אלא על ידי צבר קנוני או צבר גרנד קאנוני (צבר קאנוני גדול) במקום. האחרון, הצבר הגרנד קנוני, מתאר המערכות אשר יכולות גם להחליף חלקיקים עם סביבתן (תוך שמירה על שיווי משקל).
תכונות
[עריכת קוד מקור | עריכה]- תחת שיווי משקל סטטיסטי (במצב יציב): הצבר המיקרוקנוני אינו מתפתח עם הזמן, אף על פי שכל מרכיבי הצבר נמצאים בתנועה. הסיבה לכך היא שהצבר מוגדר אך ורק כפונקציה של הגדלים הנשמרים של המערכת .[1]
- אנטרופיית מידע מקסימלית: עבור מערכת מכנית נתונה (N, V קבועים) עם טווח נתון של אנרגיה, התפלגות אחידה של הסתברות בין מיקרומצבים שונים (כבהגדרת הצבר המיקרוקנוני) ממקסמת את התוחלת עבור הצבר.[1]
- עבור הצבר המיקרוקנוני ניתן להגדיר שלושה גדלים שונים הנקראים "אנטרופיה".[2] כל אחד מהם יכול להיות מוגדר בעזרת הפונקציית נפח המצבים , אשר מונה את כלל המצבים בעלי אנרגיה נמוכה מ־E (להגדרה המתמטית של v ראה סעיף מינוח מדויק):
- אנטרופיית בולצמן[הערה 1]
- אנטרופיה נפחית
- אנטרופיה משטחית
- אנטרופיית בולצמן[הערה 1]
- "טמפרטורות" שונות ניתנות להגדרה על פי ההאנטרופיות השונות:
- האנלוגיה בין גדלים אלה והתרמודינמיקה אינן מושלמות, כפי שנדון להלן.
הקבלות תרמודינמיות
[עריכת קוד מקור | עריכה]עבודות מוקדמות של לודוויג בולצמן במכניקה הסטטיסטית הובילה לניסוח נוסחת האנטרופיה הקרויה על שמו למערכת בעלת אנרגיה כוללת נתונה, , כאשר W הוא מספר המצבים האפשריים הנפרדים, הנגישים למערכת באנרגיה הנתונה. בולצמן לא פירט לעומק מה מהווה בדיוק מַעֲרָךְ של מצבים שונים של המערכת, מלבד במקרה המיוחד של גז אידיאלי. נושא זה נחקר על ידי ג'וסיה וילארד גיבס, אשר פיתח את המכניקה הסטטיסטית המוכללת עבור מערכות מכניות כלשהן, והגדיר את הצבר המיקרוקנוני המתואר במאמר זה.[1] גיבס חקר בקפידה את האנלוגיות בין הצבר המיקרוקנוני למדע התרמודינמיקה, ובמיוחד כיצד אנלוגיות אלו קורסות במערכות של כמה דרגות חופש. הוא הציג שתי הגדרות נוספות לאנטרופיה מיקרוקנונית שאינן תלויות ב־ω – אנטרופיית הנפח ואנטרופיית השטח שתוארו לעיל. (שים לב כי אנטרופיית פני השטח שונה אנטרופיה בולצמן רק על בצמצום של ω.)
האנטרופיה הנפחית, Sv, והטמפרטורה הנובעת ממנה, Tv, יוצרות אנלוגיה קרובה לאנטרופיה ולטמפרטורה התרמודינמיות. ניתן להראות בדיוק כי:
כצפוי על פי החוק הראשון של התרמודינמיקה. (⟨P⟩ הוא הלחץ הממוצע של הצבר). ניתן למצוא משוואה דומה לאנטרופיית פני השטח (בולצמן) ול־Ts המשויכת אליה, אולם "הלחץ" המתקבל ממשוואה זו הוא גודל מורכב שאיננו קשור ללחץ הממוצע בצבר.
האנלוגיה של Tv ו־Ts לטמפרטורה איננה משביעת רצון לחלוטין ומחוץ לגבול התרמודינמי מתקבלים מספר ממצאי שווא.
- תוצאה לא טריוויאלית של שילוב שתי מערכות: ניתן להביא שתי מערכות, אשר כל אחת מתוארת בניפרד על ידי צבר מיקרוקנוני, למגע תרמי ולאפשר הגעה לשיווי משקל כך שהמערכת המשולבת תתואר גם היא על ידי צבר מיקרוקנוני. עם זאת, לא ניתן לחזות את זרימת האנרגיה בין שתי המערכות בהתבסס על הטמפרטורות ההתחלתיות. גם כאשר הטמפרטורות ההתחלתיות שוות, ייתכן שתעבור ביניהן אנרגיה. יתר על כן, T של המערכת המשולבת שונה מהערכים ההתחלתיים. זה סותר את האינטואיציה כי הטמפרטורה צריכה להיות גודל אינטנסיבי וכי שתי מערכות שוות טמפרטורה לא צריכות להיות מושפעות ממגע תרמי ביניהן.
- התנהגות מוזרה במערכות של מספר חלקיקים: תוצאות רבות, כגון חוק החלוקה השווה המיקרוקנוני, דורשות קיזוז של דרגת חופש אחת או שתיים כאשר הן נכתבות במונחים של Ts. במערכות קטנות קיזוז זה הוא משמעותי, לכן כשלוקחים את Ss כאנטרופיה האנלוגית מספר חריגים צריכים להילקח בחשבון עבור מערכות עם דרגה אחת או שתיים של חופש.[1]
- קבלת טמפרטורות שליליות כוזבות: Ts שלילי מתרחשת בכל פעם שצפיפות המצבים יורדת עם אנרגיה. במערכות מסוימות צפיפות המצבים אינה מונוטונית עם אנרגיה, ולכן Ts יכולה לשנות סימן מספר פעמים כשהאנרגיה גדלה.[3][4]
הפתרון המועדף לבעיות אלה הוא להימנע משימוש בצבר המיקרו־קנוני. במקרים מציאותיים רבים המערכת מווסתת על ידי אמבט חום, כך האנרגיה אינה ידועה במדויק. לכן, תיאור מדויק יותר הוא הצבר הקנוני או הצבר הקאנוני הגדול, שניהם בעלי התאמה מלאה לתרמודינמיקה.[5]
מינוח מדויק
[עריכת קוד מקור | עריכה]הביטוי המתמטי המדויק להרכב סטטיסטי תלוי בסוג המכניקה הנבדקת – קוונטית או קלאסית – מאחר שהרעיון של "מיקרו־מצב" שונה במידה ניכרת בשני מקרים אלה. במכניקת הקוואנטים, לכסון מספק קבוצה בדידה של מיקרומצבים עם אנרגיות ספציפיות. ואילו במקרה המכני הקלאסי יש לבצע אינטגרל על מרחב המצבים הקנוני ("מרחב הפאזה", "phase space"), ואת גודל המיקרומצבים (עידון החלוקה) במרחב המצבים ניתן לבחור באופן שרירותי במקצת.
לשם בניית הצבר המיקרוקנוני, בכל אחת משתי המכניקות, יש להגדיר תחילה את טווח האנרגיה. בביטוי מטה הפונקציה (פונקציה של H, בעלת קיצון ב־E, עם רוחב ω) תשמש לייצוג טווח האנרגיה בו יכללו המצבים. דוגמה לפונקציה מעין זו תהיה:[1]
או פונקציה חלקה יותר:
במכניקה קוונטית
[עריכת קוד מקור | עריכה]
 ערך מורחב – אופרטור הצפיפות
ערך מורחב – אופרטור הצפיפות
במכניקת הקוונטים צברים מיוצגים על ידי מטריצת צפיפות, מסומנת על ידי . צבר מיקרוקנוני יכול להיכתב בסימון דיראק, בעזרת המצבים העצמיים של האנגיה והאנרגיות העצמיות במערכת. בהינתן בסיס שלם של מצבי־אנרגיה־עצמיים , הסדור לפי מפתח i, הצבר המיקרוקנוני ייוצג על ידי:[דרוש מקור]
כאשר Hi הן האנרגיות העצמיות הנקבעות על ידי (כאן Ĥ היא אופרטור האנרגיה הכוללת במערכת, כלומר אופרטור ההמילטוניאן). הערך של נקבע על פי הדרישה כי היא מטריצת צפיפות מנורמלת, כך ש־
פונקציית נפח המצבים (המשמשת לחישוב האנטרופיה) ניתנת על ידי
הצבר המיקרוקנוני מוגדר על ידי לקיחת הגבול של מטריצת הצפיפות כשרוחב טווח האנרגיה הולך לאפס, אולם מצב בעייתי מתרחש כאשר רוחב טווח האנרגיה הופך צר יותר nהמרווח בין רמות האנרגיה. עבור רוחב אנרגיה צר מאוד, הצבר איננו קיים כלל עבור רוב הערכים של E, שכן אין מצבים שמוכלים בטווח. כאשר הצבר כן קיים, הוא לרוב מכיל מצב אחד (או שניים), מאחר שבמערכת מורכבת רמות האנרגיה שוות אחת לשנייה רק באופן מקרי (ראו תורת המטריצות אקראיות, באנגלית, לדיון נוסף בנושא זה). יותר מכך, העלייה של פונקציית נפח המצבים היא בדידה ולא רציפה ולכן ערכי הנגזרת שלה הם רק אפס או "אינסוף", מה שמקשה על הגדרת צפיפות המצבים. ניתן לפתור בעיה זו על ידי הימנעות מלקחת את רוחב טווח האנרגיה לאפס באופן מוחלט והחלקה של פונקציית נפח המצבים, ברם זה הופך את הגדרת הצבר למסובכת עוד יותר, שכן זה מחייב לציין ולהתחשב ברוחב טווח האנרגיה בנוסף למשתנים אחרים (יחד: "צבר ").
במכניקה הקלאסית
[עריכת קוד מקור | עריכה]במכניקה קלאסית, צבר מיוצג על ידי פונקציית צפיפות־הסתברות משותפת המוגדרת על מרחב הפזה של המערכת.[1] במרחב הפזה יש n קואורדינטות מוכללות המסומנות ב־, ו־n משתני התנע הצמודים־קנונית שלהן, . פונקציית צפיפות הסתברות של הצבר המקרוקנוני היא:
כאשר
- היא האנרגיה הכוללת (ההמילטוניאנית) של המערכת, פונקציה של המצב (הפזה)
- הוא קבוע שרירותי בעל יחידות של זמן×אנרגיה, קובע את "גודלו" של מיקרו־מצב יחיד ונותן ל־ את הממדים נכונים.[הערה 2]
- הוא גורם תיקון לספירת יתר, המשמש לעיתים קרובות עבור מערכות חלקיקים בהן חלקיקים זהים מסוגלים לשנות מקום אחד עם השני.[הערה 3]
גם כאן, הערך של נקבע על ידי דרישה כי היא פונקציית צפיפות הסתברות מנורמלת:
אינטגרל זה מחושב מעל מרחב הפזה.
הפונקציית נפח המצבים (המשמשת לחישוב האנטרופיה) מוגדרת על ידי:
כאשר רוחב טווח האנרגיה שואף לאפס, ערכו של יורד באופן יחסי ל־ כך: .
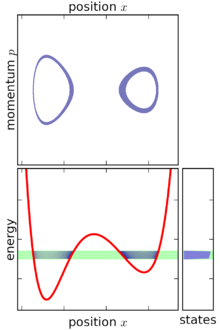
בהתבסס על ההגדרות לעיל, ניתן לתאר את הצבר המקרוקנוני כקליפה דקה במרחב הפזה, בעלת עובי אינפיניטסימלי סביב השטח שווה אנרגיה. למרות שהמיקרומצבים שכלולים בצבר המיקרוקנוני כולם בהכרח על משטח זה, פיזורם וצפיפותם על המשטח איננה חייבת להיות אחידה: אם גרדיינט האנרגיה במרחב הפזה משתנה, אז הצבר "עבה יותר" (מרוכז יותר) בחלקים מסוימים של המשטח מאשר באחרים. תכונה זו היא תוצאה בלתי נמנעת של הדרישה כי הצבר המיקרוקנוני יהיה צבר יציב (steady-state ensemble).
הערות שוליים
[עריכת קוד מקור | עריכה]- ^ SB היא אנטרופיית המידע, או אנטרופיית גיבס, עבור המקרה הספציפי של ההרכב המיקרו-קנוני. שימו לב שזה תלוי ברוחב האנרגיה ω.
- ^ (הערה היסטורית) במקור הגדיר גיבס את הצבר כך שבאופן יעיל , ומכך שהתלוי רק בערכים של כמויות תרמודינמיות כמו אנטרופיה ופוטנציאל כימי. מאז הופעת מכניקת הקוונטים, נבחר לעיתים קרובות להיות לקבוע פלנק כדי ליצור התכתבות ועיקביות עם מכניקת הקוונטים.
- ^ במערכת של חלקיקים זהים, (עצרת של ).גורם זה מתקן ספירה חוזרת של מצבים זהים פיזיקלית
הערות שוליים
[עריכת קוד מקור | עריכה]- ^ 1 2 3 4 5 6 7 8 9 גיבס, ג'וסיה וילארד (1902). Elementary Principles in Statistical Mechanics. ניו יורק: Charles Scribner's Sons.
- ^ Huang, Kerson (1987). Statistical Mechanics. Wiley. p. 134. ISBN 0471815187.
- ^ Jörn Dunkel; Stefan Hilbert (2013). "Inconsistent thermostatistics and negative absolute temperatures". Nature Physics. 10: 67–72. arXiv:1304.2066. Bibcode:2014NatPh..10...67D. doi:10.1038/nphys2815.
- ^ ראה עוד הפניות ב: https://sites.google.com/site/entropysurfaceorvolume/
- ^ Tolman, R. C. (1938). The Principles of Statistical Mechanics. Oxford University Press.
| מכניקה סטטיסטית | ||
|---|---|---|
| תאוריה | עקרון גידול האנטרופיה • ergodic theory | |
| תרמודינמיקה סטטיסטית | צברים • פונקציית חלוקה • משוואות מצב • פוטנציאלים תרמודינמיים: (U • H • F • G) • קשרי מקסוול | |
| מודל סטטיסטי | Ferromagnetism models (איזינג • פוטס • הייזנברג • חלחול EN) • חלקיקים בעלי שדה כוחות (כוחות דלדול EN • פוטנציאל לנארד-ג'ונס) | |
| גישות מתמטיות | משוואת בולצמן • משפט־H • משוואת ולסוב • מדרג BBGKY • תהליך סטוכסטי • תורת שדה ממוצע ותורת השדות הקונפורמית | |
| תופעות קריטיות | מעבר פאזה • אקספוננט קריטי (מרחק קורלציה • size scaling) | |
| אנטרופיה | בולצמן • שאנון • צאליס • רניי • פון נוימן | |
| יישומים | תורת השדות הסטטיסטית (חלקיקים יסודיים • נוזלי־על) • פיזיקה של חומר מעובה • מערכות מורכבות (כאוס • תורת האינפורמציה • אנטרופיה בתרמודינמיקה ובתורת האינפורמציה • מכונת בולצמן) | |








































![{\displaystyle h=1_{[energy\ unit]\times [time\ unit]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbc47ca73d9f2919c7df276d4630ec5f4755c9bd)

