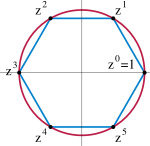
Alternáló csoport
Az n-nel indexelt alternáló csoport egy n elemű halmaz páros permutációit tartalmazza. A művelet a permutációk szorzása, vagyis egymás utáni elvégzése. Többnyire egyszerűen csak az An alternáló csoportról beszélnek.
Az n indexű alternáló csoport a megfelelő Sn szimmetrikus csoport normálosztója. Ha n legalább 5, akkor a megfelelő alternáló csoport egyszerű, vagyis nincs nem triviális normálosztója. Így a megfelelő Sn szimmetrikus csoport nem feloldható, ezért a legalább ötödfokú egyenletek nem oldhatók meg gyökjelekkel. Ez az Abel-Ruffini-tétel.
Tulajdonságai
[szerkesztés]- Alternáló csoport csak legalább n=2 indexre van értelmezve.
- Az An alternáló csoport rendje .
- Az alternáló csoportok közül csak A2 és A3 Abel.
- An egyszerű, ha n legalább 5. Az A5 a legkisebb nem kommutatív egyszerű csoport, egyben az ikozaéder szimmetriacsoportja.
- An indexe 2 a megfelelő Sn permutációcsoportban, ezért normálosztó is benne. Ha n legalább 5, akkor az egyetlen nem triviális normálosztó.
- Sőt, An az Sn kommutátorcsoportja.
Az alternáló csoport generálható a három hosszú ciklikus permutációkkal:
Ezek a három hosszú ciklusok valóban párosak, mivel felírhatók két transzpozíció szorzataként:
A többi páros permutáció is előáll:
- ha a két transzpozíció ugyanaz
- ha a két transzpozíció által felcserélt elemek egyike megegyezik
- ha a két transzpozíció által felcserélt elemek különbözők.
Páros és páratlan permutációk
[szerkesztés]A páros és a páratlan permutációk az inverziószám alapján különböztethetők meg. Ha egy permutációban a nagyobb elem előbbre kerül, mint egy kisebb, akkor az inverzió. Például a permutációban a 3 az 1 és a 2 előtt áll; ez két inverzió. Mivel nincs több, ezért a permutáció inverziószáma 2. Ez páros, így a permutáció is páros.
Ha az inverziószám páros, a permutáció páros; ha páratlan, akkor a permutáció is páratlan. Szokás a permutáció előjeléről beszélni; ez páros permutációkra pozitív, páratlanokra negatív. Ha -1 hatványaként definiálják, akkor ez egy homomorfizmus a kételemű csoportba, ugyanis két permutáció szorzatának előjele a permutációk előjelének szorzata.
Tényleg csoport
[szerkesztés]Állítás: A páros permutációk csoportot alkotnak.
Bizonyítás:
- Az identitás páros permutáció, mivel egy transzpozíció önmagával vett szorzata identitás.
- A páros permutációk szorzata is páros, hiszen két permutáció szorzatának előjele a permutációk előjelének szorzata.
Ezekkel a tulajdonságokkal Sn-ből a következőket örökli:
- Asszociativitás
- Az identitás jobb és bal oldali egységelem
- Az inverz is páros, mert megkapható a megfelelő transzpozíciók fordított sorrendben vett szorzataként.
Zártság bővebben
[szerkesztés]Transzpozíciók
[szerkesztés]A transzpozíciók olyan permutációk, amik két elemet cserélnek fel, a többit fixen hagyják. Például a az 5-öt a 3-mal cseréli fel. Általában bármely permutációból el lehet jutni egy másikba véges sok transzpozícióval való szorzással, sőt ez elérhető olyan transzpozíciók szorzásával is, amik két szomszédos elemet cserélnek fel. Például, ha egy könyvtárban csak a szomszédos könyveket cserélik fel, akkor a könyvek teljesen összekeveredhetnek.
Speciálisan, az identikus transzpozícióból is elő lehet állítani bármely permutációt transzpozíciók szorzataként. Ezt úgy is mondjuk, hogy a transzpozíciók generálják a teljes szimmetrikus csoportot. Ez a felírás nyilván nem egyértelmű, hiszen bármely két transzpozíció közé beszúrhatjuk kétszer ugyanazt a transzpozíciót, amik éppen az identitást adják.
Transzpozíciók és inverziószám
[szerkesztés]Egy transzpozícióval való szorzással az inverziószám páratlan számmal változik meg, így párosból páratlan, páratlanból páros lesz.
Legyen az eredeti permutáció
és az új:
- Ha x < z, akkor hozzájárulásuk az inverziók számához -1, különben 1
- A többi hozzájárulás páros:
- Ha y1 a középső elem, a hozzájárulás +2 vagy -2
- Különben a hozzájárulás 0
Összegezve, páratlan sok transzpozícióval való szorzás a páros permutációt páratlanná, a páratlant párossá teszi. Páros sok transzpozícióval vett szorzat viszont megőrzi a szorzat páros, vagy páratlan voltát.
Transzpozíciók és zártság
[szerkesztés]Az identitás páros volta miatt a páros permutációk páros sok transzpozíció szorzataként, a páratlanok csak páratlan sok permutáció szorzataként fejezhetők ki.
Ha p és q páros permutáció, akkor vannak és páros számok, hogy
Ezzel , tehát a szorzat páros.
Más szóval a páros permutációk megőrzik az előjelet. Hasonlóan, a páratlan permutációk megváltoztatják.
A páros permutációk inverze is páros, különben az identitás páratlan lenne, ami ellentmondás.
Források
[szerkesztés]- Christian Karpfinger, Kurt Meyberg: Algebra. Gruppen – Ringe – Körper. Spektrum Akademischer Verlag, Heidelberg 2009, ISBN 978-3-8274-2018-3, S. 108–109
- Kiss Emil: Bevezetés az algebrába