Հարաբերական Դոպլերի էֆեկտ

Նկար 1. Լույսի ալիքների աղբյուր, որը շարժվում է դեպի աջ, դիտորդների համեմատ, 0,7c արագությամբ: Հաճախականությունը ավելի բարձր է աջ կողմում գտնվող դիտորդների համար, իսկ ձախ դիտորդների համար ավելի ցածր:

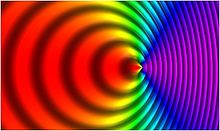
Ռելյատիվիստական (հարաբերական) Դոպլերի էֆեկտը լույսի հաճախականության(և ալիքի երկարության) փոփոխությունն է, որն առաջանում է աղբյուրի և դիտորդի հարաբերական շարժուման հետևանքով (ինչպես դասական Դոպլերի էֆեկտում ), որտեղ հաշվի են առնվում նաև հարաբերականության հատուկ տեսության կողմից նկարագրված էֆեկտները։

Ռելյատիվիստական Դոպլերի էֆեկտը տարբերվում է ոչ ռելյատիվիստական Դոպլերի էֆեկտից, քանի որ հավասարումները ներառում են ժամանակի դանդաղումը, որը հանդիսանում է հարաբերականության հատուկ տեսության էֆեկտը, սակայն չեն ներառում տարածվող միջավայրը որպես հղման կետ։ Նրանք նկարագրում են դիտարկվող հաճախությունների ընդհանուր տարբերությունը և համապատասխանում են Լորենցի պահանջվող համաչափությանը։

Աստղագետները գիտեն կարմիր / կապույտ շեղումների երեք աղբյուրներ՝ Դոպլերի շեղումներ, գրավիտացիոն կարմիր շեղումներ (գրավերիտացիոն դաշտից դուրս եկող լույսի պատճառով); և տիեզերական ընդլայնում (որտեղ տարածությունն ինքն է ձգվում)։ Այս հոդվածը վերաբերում է միայն Դոպլերային շեղումներին։

Հիմնական արդյունքների ամփոփում

Հետևյալ աղյուսակում ենթադրվում է, որ համար ${\displaystyle \beta =v/c>0}$ դիտորդը և աղբյուրը հեռանում են միմյանցից, որտեղ ${\displaystyle v}$-ն հարաբերական, իսկ ${\displaystyle c}$-ն լույսի արագություններն են։

Դեպք	Բանաձև	Նշումներ
Դոպլերի ռելյատիվիստական երկայնական էֆեկտը	${\displaystyle {\frac {\lambda _{r}}{\lambda _{s}}}={\frac {f_{s}}{f_{r}}}={\sqrt {\frac {1+\beta }{1-\beta }}}}$
լայնակի դոպլեր էֆեկտ,երկրաչափական մոտեցումը	${\displaystyle f_{r}=\gamma f_{s}}$	Կապույտ շեղում
լայնակի դոպլեր էֆեկտ,տեսողական ամենամոտ կետ	${\displaystyle f_{r}={\frac {f_{s}}{\gamma }}}$	Կարմիր շեղում
TDE, ՝աղբյուրի շրջանաձև շարժումը դիտորդի շուրջ	${\displaystyle f_{r}=\gamma f_{s}}$	Կապույտ շեղում
TDE, աղբյուրի և դիտորդի շրջանաձև շարժումը հիմնական կենտրոնի շուրջ	${\displaystyle f_{r}={\frac {f_{s}}{\gamma }}}$	Կարմիր շեղում
TDE, աղբյուրի և դիտորդի շրջանաձև շարժումը ընդհանուր կենտրոնի շուրջ	${\displaystyle {\frac {\nu '}{\nu }}=\left({\frac {1-R^{2}\omega ^{2}}{1-R'^{2}\omega ^{2}}}\right)^{1/2}}$	Դոպլերային տեղաշարժ չկա </br> երբ ${\displaystyle R=R'}$
Շարժում կամայական ուղղությամբ չափված դիտորդի կողմից	${\displaystyle f_{r}={\frac {f_{s}}{\gamma \left(1+\beta \cos \theta _{r}\right)}}}$
Շարժում կամայական ուղղությամբ<br id="mwXA"> չափված աղբյուրի մոտակայքից	${\displaystyle f_{r}=\gamma \left(1-\beta \cos \theta _{s}\right)f_{s}}$

Ածանցում

Հարաբերական երկայնական Դոպլերի էֆեկտ

Հարաբերական դոպլերային տեղաշարժը երկայնական դեպքի համար, որտեղ աղբյուրը և ստացողը ուղղակիորեն շարժվում են իրար ընդառաջ կամ իրար հակառակ, հաճախ դիտարկվում է որպես դասական երևույթ, որը սակայն փոխվում է ժամանակի դանդաղեցման տերմինի ավելացմամբ^[1][2]։ Սա այն մոտեցումն է, որն օգտագործվում է առաջին կուրսի ֆիզիկայի կամ մեխանիկայի դասագրքերում, ինչպիսիք են Ֆեյնմանի^[3] կամ Մորինի դասագրքերը^[4]։

Հետևելով հարաբերական Դոպլերի էֆեկտի երկայնական դեպքի ստացման այս մոտեցմանը, ենթադրենք, որ ստացողը և աղբյուրը հեռանում են միմյանցից հարաբերական ${\displaystyle v\,}$ արագությամբ, որը աղբյուրի կամ ընդունիչի կողմից արձակած ալիքի երկարության արագությունն է, չափված դիտորդի (Այստեղ, եթե ստացողը և աղբյուրը շարժվում են միմյանց ընդառաջ ընդունված նշանի կոնվենցիայում ${\displaystyle v\,}$-ն բացասական է,)։

Խնդիրը դիտարկեք աղբյուրի հղման շրջանակում:

Ենթադրենք, մեկ ալիքային ճակատը հասնում է դիտորդին։ Հետևաբար հաջորդ ալիքը գտնվում է դիտորդից ${\displaystyle \lambda _{s}=c/f_{s}\,}$հեռավորության վրա (որտեղ ${\displaystyle \lambda _{s}\,}$ ալիքի երկարությունն է, ${\displaystyle f_{s}\,}$ աղբյուրի արձակած ալիքի հաճախությունը, իսկ ${\displaystyle c\,}$-ն լույսի արագությունը)։

Ալիքային ճակատը շարժվում է ${\displaystyle c\,}$ արագությամբ , բայց միևնույն ժամանակ ընդունիչը ${\displaystyle t_{r,s}}$ժամանակի ընթացքում ${\displaystyle v}$ արագությամբ հեռանում է որը լույսի ալիքների՝ ընդունիչին դիպչող ժամանակաշրջանն է, ինչպես նկատվում է աղբյուրի շրջանակում։ Այսպիսով,

$${\displaystyle \lambda _{s}+vt_{r,s}=ct_{r,s}\Longleftrightarrow \lambda _{s}=ct_{r,s}(1-v/c)\Longleftrightarrow t_{r,s}={\frac {1}{f_{s}(1-\beta )}},}$$$${\displaystyle \lambda _{s}+vt_{r,s}=ct_{r,s}\Longleftrightarrow \lambda _{s}=ct_{r,s}(1-v/c)\Longleftrightarrow t_{r,s}={\frac {1}{f_{s}(1-\beta )}},}$$$${\displaystyle \lambda _{s}+vt_{r,s}=ct_{r,s}\Longleftrightarrow \lambda _{s}=ct_{r,s}(1-v/c)\Longleftrightarrow t_{r,s}={\frac {1}{f_{s}(1-\beta )}},}$$$${\displaystyle \lambda _{s}+vt_{r,s}=ct_{r,s}\Longleftrightarrow \lambda _{s}=ct_{r,s}(1-v/c)\Longleftrightarrow t_{r,s}={\frac {1}{f_{s}(1-\beta )}},}$$

որտեղ ${\displaystyle \beta =v/c\,}$ ստացողի արագությունն է, որն հաշվարկված է լույսի արագության նկատմամբ։ Համապատասխանաբար ${\displaystyle f_{r,s}}$, հաճախականությունը, որով ալիքի ճակատները հասնում են դիտորդին, հետևյալն է.$${\displaystyle f_{r,s}=1/t_{r,s}=f_{s}(1-\beta ).}$$Մինչ այժմ, անշարժ աղբյուրով և շարժական դիտորդով հավասարումները նույնական են եղել դասական Դոպլերի էֆեկտի հավասարումների հետ։

Այնուամենայնիվ, ռելյատիվիստական էֆեկտների պատճառով ընդունիչի վրա տեղադրած ժամացույցներում աղբյուրի վրա տեղակայված ժամացույցների համեմատժամանակի դանդաղում է նկատվել . ${\displaystyle t_{r}=t_{r,s}/\gamma }$, որտեղ ${\textstyle \gamma =1/{\sqrt {1-\beta ^{2}}}}$ Լորենցի գործոնն է։ Որպեսզի իմանանք, թե որ ժամն է դանդաղած, հիշում ենք ${\displaystyle t_{r,s}}$, որ դա այն շրջանի ժամանակն է, որում աղբյուրը հանգստանում է։ Հետևաբար ստացողի կչափի հետևյալ հաճախությունը՝

Eq. 1: ${\displaystyle f_{r}=f_{r,s}\gamma }$ ${\displaystyle ={\frac {1-\beta }{\sqrt {1-\beta ^{2}}}}f_{s}}$ ${\displaystyle ={\sqrt {\frac {1-\beta }{1+\beta }}}\,f_{s}.}$

հարաբերակցությունը

${\displaystyle {\frac {f_{s}}{f_{r}}}={\sqrt {\frac {1+\beta }{1-\beta }}}}$

կոչվում է աղբյուրի Դոպլերի գործոն ՝ ստացողի նկատմամբ։ (Այս տերմինաբանությունը հատկապես տարածված է աստղաֆիզիկա առարկայում. տե՛ս հարաբերական ճառագայթում)։

Համապատասխան ալիքի երկարությունները կապված են

Eq. 2:    ${\displaystyle {\frac {\lambda _{r}}{\lambda _{s}}}={\frac {f_{s}}{f_{r}}}={\sqrt {\frac {1+\beta }{1-\beta }}},}$

Դոպլերի հարաբերական շեղման նույնական արտահայտություններ են ստացվում դիտորդի շրջակայքում շարժվող աղբյուրի վերաբերյալ վերլուծություն կատարելիս: Սա համընկնում է հարաբերականության սկզբունքի հետ. արդյունքը չի կարող կախված լինել նրանից, թե որ առարկան է համարվում հանգիստ վիճակում։ Ի հակադրություն դրա, դասական ոչ հարաբերական Դոպլերի էֆեկտը կախված է աղբյուրի կամ դիտորդի հանգստի վիճակից։

Լայնական Դոպլերի էֆեկտ

Ենթադրենք, որ աղբյուրը և դիտորդը երկուսն էլ մոտենում են միատեսակ իներցիոն շարժումով՝ չբախվելով միմյանց։ Լայնակի Դոպլերի էֆեկտը (ԼԴԷ) կարող է վերաբերել (ա) հարաբերականության հատուկ տեսության կողմից կանխատեսված անվանական կապույտ շեղմանը, որը տեղի է ունենում, երբ աղբյուրը և ստացողը գտնվում են իրարից ամենամոտ հեռավորության վրա, կամ երբ (բ) հարաբերականության հատուկ տեսության կողմից կանխատեսված կարմիր շեղուման ժամանակ ստացողը տեսնում է, որ էմիտը գտնվում է իրեն ամենամոտ հեռավորության վրա^[4]։ Լայնակի Դոպլերի էֆեկտը հարաբերականության հատուկ տեսության հիմնական կանխատեսումներից է։

Այն փաստը, թե գիտական զեկույցը նկարագրում է TDE-ն, որպես կարմիր թե կապույտ շեղում, կախված է փորձարարական դասավորության մանրամասներից։ Օրինակ, 1907 թվականին Էյնշտեյնի կողմից տրված TDE-ի բնօրինակի նկարագրությունը բացահայտում էր այն«ջրանցքի ճառագայթների» (դրական իոնների փունջ,որոնք ստեղծվում են գազային ի կողմից կենտրոնին (մոտակա կետին), որը ստեղծվում է գազի արտանետման խողովակների կողմից։ Հարաբերականության հատուկ տեսության համաձայն՝ շարժվող իոնների արտանետվող հաճախականությունը կնվազի Լորենցի գործակցով, այնպես որ ստացված հաճախականությունը նույն գործակցով կնվազի (կարմիր տեղաշարժ)^{[p 1]}։ ^[5]

Մյուս կողմից, Կյունդիգը (1963) նկարագրել է մի փորձ, որտեղ Մյոսբաուերի կլանիչը արագ, շրջանաձև ուղեծրով պտտվում էր կենտրոնական Մյոսբաուերի աղբյուրի շուրջ^{[p 3]}։ Ինչպես բացատրվում է ստորև, այս փորձնական դասավորությունը հանգեցրեց Կյունդիգի կողմից կապույտ շեղման չափմանը։

Աղբյուրը և դիտորդը գտնվում են իրենց ամենամոտ հասանելիության կետերում

Նկար 2.Աղբյուրը և դիտորդը գտնվում են իրենց ամենամոտ հասանելիության կետերում ա) Դիտորդի տեսանկյունից. բ) Աղբյուրի տեսանկյունից:

Այս սցենարում հասանելիության ամենամոտ կետը ներկայացնում է այն պահը, երբ ժամանակի ընթացքում հեռավորության փոփոխություն չկա։ Նկար 2-ը ցույց է տալիս, որ այս սցենարի վերլուծության հեշտությունը կախված է այն դեպքից, որում այն վերլուծվում է^[4]։

• Նկ.2 ա. Եթե մենք վերլուծում ենք դեպքը ստացողի շրջանակում, ապա մենք գտնում ենք, որ վերլուծությունը ավելի բարդ է, քան պետք է լինի։ երբ լույսը հասնում է դիտորդին երկնային օբյեկտի տեսանելի դիրքը ժամանակի ընթացքում օբյեկտի շարժման պատճառով տեղաշարժվում է իր իրական դիրքից (կամ երկրաչափական դիրքից)։ Աղբյուրում դիտորդի տեսանկյունից ժամանակի դանդաղում կդիտվի, սակայն այս ժամանակի դանդաղումով ենթադրվող կարմիր շեղումը կփոխարինվի կապույտ շեղումով` ստացողի և աղբյուրի ակնհայտ դիրքի միջև հարաբերական շարժման երկայնական բաղադրիչի պատճառով։
• Նկ. 2բ. Շատ ավելի հեշտ է, եթե դրա փոխարեն դեպքը վերլուծենք աղբյուրի կողմից։ Աղբյուրը խնդրի պայմաններից գիտի, որ դիտորդը գտնվում է իրեն ամենամոտ կետում։ Դա նշանակում է, որ դիտորդըը չունի շարժման երկայնական բաղադրիչ, որը բարդացնում է վերլուծությունը։ (այսինքն dr/dt = 0, որտեղ r-ը ստացողի և աղբյուրի միջև եղած հեռավորությունն է), քանի որ դիտորդի ժամացույցներում աղբյուրի համեմատ դիտվել է ժամանակ դանդաղում, լույսը, որը ստանում է դիտորդը, գամմայի գործակցով փոխվում է կապույտ շեղումի։ Այլ կերպ ասած՝

հ. 3: ${\displaystyle f_{r}=\gamma f_{s}}$

Դիտորդը աղբյուրը տեսնում է որպես ամենամոտ կետ

Նկար 3. Դոպլերի լայնակի շեղումը այն դեպքի համար, երբ ստացողը տեսնում է, որ աղբյուրը գտնվում է իրեն ամենամոտ կետում:

Այս դեպքը համարժեք է նրան, որ ստացողը նայում է աղբյուրին ուղիղ անկյան տակ։ Այս սցենարի վերլուծությունը լավագույնս կատարվում է դիտորդի տեսանկյունից։ Նկար 3-ը ցույց է տալիս, որ չնայած աղբյուրի տեղաշարժին, դիտորդը լուսավորվում է այն պահին, երբ աղբյուրը ամենամոտն է իրեն^[4]։ Աղբյուրի արձակած լույսի հաճախությունը, որն արտանետվում է նրան ամենամոտ կետից, փոխվում է կարմիր շեղման հետ մեկտեղ, քանի որ աղբյուրում և դիտորդի շրջակայքում տեղակայված ժամացույցները շարժվում են որոշակի ժամանակի դանդաղումով, և դրա շարժման երկայնական բաղադրիչը բացակայում է։

Հ. 4: ${\displaystyle f_{r}={\frac {f_{s}}{\gamma }}}$

Գրականությունում Դոպլերի լայնակի շեղման մասին ինֆորմացիայի մեծ մասը վերլուծում է աղբյուրի նկատմամբ ուղիղ անկյան տակ գտնվող դիտորդի տեսանկյունից՝ այդպիսով տեսնելով աղբյուրը իր ամենամոտ կետում և դիտելով կարմիր շեղում։

Հաճախության զրոյական շեղման կետ

Նկար 4. Զրոյական հաճախության շեղումը տեղի է ունենում իմպուլսի միջոցով, որն անցնում է աղբյուրից մինչև դիտորդ ամենակարճ հեռավորությունը։

Երբ իներցիալ շարժվող աղբյուրը և դիտորդը երկրաչափորեն մոտ են միմյանց, դիտորդը նկատում է կապույտ շեղումը, մինչդեռ երբ դիտորդը տեսնում է աղբյուրը որպես ամենամոտ կետ, նա դիտում է կարմիր շեղում։ Այս ամենից հետևում է, որ գոյություն ունի այնպիսի մի կետ, որտեղ կապույտ շեղումը փոխվում է կարմիր շեղման։ Նկ. 2-ում, ազդանշանը շարժվում է ուղղահայաց դեպի դիտորդ և փոխվում է կապույտ շեղման։ Նկ.3-ում, ազդանշանը շարժվում է ուղղահայաց դեպի աղբյուր և դիտվում է կարմիր շեղում։

Ինչպես երևում է Նկ.4-ում, զրոյական հաճախության շեղումը տեղի է ունենում իմպուլսի պատճառով, որն անցնում է ամենակարճ հեռավորությունը աղբյուրից մինչև դիտորդ։Եթե դիտենք այն պահը, երբ աղբյուրը և դիտորդն ունեն նույն արագությունը, ապա իմպուլսը ուղղահայաց կդառնա աղբյուրի ուղղուն, հետևաբար այն ուղղահայաց կլինի նաև դիտորդի ուղուն։ Իմպուլսը որողակի ճանպարհ է մինչև մոտեցման կետը, և այն ստացվում է մի փոքր հետո:^[6]

Մի առարկան մյուսի շուրջ շրջանաձև շարժման մեջ է

Նկար 5. Լայնակի դոպլեր էֆեկտը երկու սցենարի համար. ա) աղբյուրի շուրջ շրջանաձև շարժվող ստացողը. բ) ստացողի շուրջ շրջանաձև շարժվող աղբյուրը:

Նկ. 5-ը ցույց է տալիս այս սցենարի երկու տարբերակ։ Երկու տարբերակներն էլ կարող են վերլուծվել՝ օգտագործելով ժամանակի դանդաղեցման վերաբերյալ պարզ փաստարկներ^[4]։ Նկար 5ա-ն ըստ էության համարժեք է 2բ նկարում նկարագրված սցենարին, սակայն ստացողը դիտում է լույսը աղբյուրից, քանի որ այն փոխվում է կապույտ շեղման ${\displaystyle \gamma }$ գործակցով։ Իսկ նկար 5բ-ն ըստ էության համարժեք է 3-րդ նկարում նկարագրված դեպքին, երբ լույսը ունի կարմիր շեղում։

Այստեղ միակ թվացյալ բարդությունն այն է, որ պտտվող մարմինները արագացող շարժման մեջ են։ Արագացող մասնիկը չունի իներցիոն փակ համակարգ, որում միշտ կգտնվի հանգստի վիճակում։ Սակայն, միշտ հնարավոր է գտնել այնպիսի ժամանակահատված, որի ընթացքում մասնիկը մի պահ կգտնվի իներցիոն փակ համակարգում։ Այս համակարգը՝ <i id="mwAQI">ակնթարթորեն շարժվող մասնիկի համակարգն է</i> (MCRF), որը թույլ է տալիս կիրառել հարաբերական հատուկ տեսությունը արագացված մասնիկների վերլուծության համար։ Եթե իներցիոն համակարգում գտնվող դիտորդը նայում է արագացող ժամացույցին, ապա ժամանակի ընդլայնումը հաշվելիս կարևոր է միայն ժամացույցի ակնթարթային արագությունը^[7]։

Հակառակը, սակայն, ճիշտ չէ։ Այն դեպքը, որտեղ երկու մարմիններն էլ գտնվում են արագացված շարժման մեջ, պահանջում է մի փոքր ավելի բարդ վերլուծություն։ Այս կետը չհասկանալը հանգեցրել է շփոթության և թյուրիմացության։

Աղբյուրը և ստացողը երկուսն էլ շրջանաձև շարժման մեջ են ընդհանուր կենտրոնի շուրջ

Նկար 6. Աղբյուրը և դիտորդը տեղակայված են ռոտորի հակառակ ծայրերում՝ կենտրոնից հավասար հեռավորության վրա:

Ենթադրենք աղբյուրը և ընդունիչը գտնվում են պտտվող ռոտորի հակառակ ծայրերում, ինչպես ցույց է տրված Նկ.6-ում։ Կինեմատիկական փաստարկները (հարաբերականության հատուկ տեսությունում) և ռոտորի կեղծ գրավիտացիոն դաշտում աղբյուրի և ստացողի միջև տարբերություն չլինելու (ընդհանուր հարաբերականություն) փաստարկը, հանգեցնում են այն եզրակացության, որ աղբյուրի և ստացողի միջև չպետք է լինի Դոպլերային տեղաշարժ։

1961թ.-ին Շամպենինը և Մունը կատարեցին Մյոսբաուերի ռոտորի փորձարկումը՝ փորձարկեցին հենց այս սցենարը և պարզեցին, որ Մյոսբաուերի կլանման գործընթացը չի ազդում պտույտի վրա^{[p 4]}։ Ինչից էլ նրանք եզրակացրեցին, որ իրենց բացահայտումները հաստատում են հարաբերականության հատուկ տեսությունը։

Այս եզրակացությունը որոշ հակասություններ առաջացրեց։ Հարաբերականության համառ քննադատը պնդում էին, որ թեև փորձը համընկնում էր հարաբերականության ընդհանուր տեսությանը, սակայն այն հերքում էր այն։ Ըստ նրա արտանետիչը և կլանիչը գտնվում էին միատեսակ հարաբերական շարժման մեջ, ուստի հարաբերականության հատուկ տեսությունը պահանջում էր դիտարկել Դոպլերի տեղաշարժ։ Քննադատի այս փաստարկի սխալն այն էր, (ինչպես ցույց է տրված «Զրոյական հաճախականության տեղաշարժի կետ» բաժնում) որ Դոպլերային շեղումը միշտ չէ, որ պետք է դիտարկվի որպես երկու համակարգ, որոնք գտնվում են միատեսակ հարաբերական շարժման մեջ^[8]։ Ավելին, ինչպես ցույց է տված «Աղբյուրը և ստացողը գտնվում են իրենց ամենամոտ հեռավորության վրա» բաժնում։ հարաբերական տեսության վերլուծության դժվարությունը հաճախ կախված է լինում համակարգի ընտրությունից։ Դիտողի համակարգում տեսությունը վերլուծելու փորձը պահանջում է հոգնեցուցիչ հանրահաշվական վերլուծություն։ Շատ ավելի հեշտ է, լաբորատոր փորձով հաստատել Դոպլերի շեղման բացակայությունը աղբյուրի և դիտորդի միջև^[8]։

Սակայն, ըստ էության, Շեմփենիի և Մունի փորձը հարաբերականության հատուկ տեսության մեջ ոչ մի էական դեր չխաղաց։ Կարգավորման համաչափության պատճառով պարզվում է, որ միատեսակ իներցիալ համակարգում շարժվող մարմինների միջև Դոպլերի շեղումը գրեթե ցանկացած տեսության դեպքում պետք է զրոյական արդյունք տա^[8]։

Կենտրոնից հավասար հեռավորության փոխարեն, ենթադրենք, որ արտանետիչը և կլանիչը գտնվում են կենտրոնից տարբեր հեռավորությունների վրա։ Ռոտորից ${\displaystyle R'}$շառավիղ հեռավորությունում գտնվող ստացողի և ${\displaystyle R}$ շառավղի շրջանակում աղբյուրը վրա ազդող հաճախությունների քաորդը ${\displaystyle \nu '}$ է, երբ աղբյուրի ${\displaystyle \nu ,}$ հաճախությունը տրված է։

Eq. 5:    ${\displaystyle {\frac {\nu '}{\nu }}=\left({\frac {1-R^{2}\omega ^{2}}{1-R'^{2}\omega ^{2}}}\right)^{1/2}}$

որտեղ ${\displaystyle \omega }$ ռոտորի անկյունային արագությունն է։ Պարտադիր չէ, որ աղբյուրը և դիտորդը միմյանցից 180°-ի անկյան տակ լինեն,քանի որ դրանք կենտրոնի նկատմամբ կարող են լինել ցանկացած անկյան տակ^{[p 5][9]}։

Շարժում կամայական ուղղությամբ

Նկար 7. Դոպլերի տեղաշարժը աղբյուրի և դիտորդի միջև ուղղի երկայնքով, կամայական անկյան շեղման տակ։

Օգտվելով հարաբերական երկայնական դոպլեր էֆեկտում օգտագործվող վերլուծությունից կարող ենք պարզ ձևով հաշվարկել Դոպլերի տեղաշարժը այն դեպքի համար, երբ աղբյուրի և դիտորդը իներցիոն շարժուման մեջ են գտնվում են ցանկացած անկյան տակ^[2][10]։ Նկ.7-ը ներկայացնում է դեպքը դիտորդի տեասնկյունից, որտեղ աղբյուրը շարժվում է ${\displaystyle v}$ արագությամբ ${\displaystyle \theta _{r}}$անկյան տակ։ Ուղիղ գծով աղբյուրի շարժման շառավղային բաղադրիչը հավասար է ${\displaystyle v\cos {\theta _{r}}.}$

Ստորև բերված հավասարումը կարող է մեկնաբանվել, որպես դասական դոպլերային շեղում, մեկնանաբանված Լորենցի ${\displaystyle \gamma }$ գործոնով՝ անշարժ և շարժվող աղբյուրների մասին։

Eq. 6:    ${\displaystyle f_{r}={\frac {f_{s}}{\gamma \left(1+\beta \cos \theta _{r}\right)}}.}$

Այն դեպքում, երբ ${\displaystyle \theta _{r}=90^{\circ }}$ է և ստացվում է լայնակի Դոպլերի էֆեկտը.

${\displaystyle f_{r}={\frac {f_{s}}{\gamma }}.\,}$

Հարաբերականության հատուկ տեսության մասին իր 1905թ. աշխատությունում Էյնշտեյնը Դոպլերի շեղման հավասարման համար ստացավ մի փոքր այլ տեսք ունեցող հավասարում։ Նրա հավասարման մեջ փոփոխականների անունները փոխելուց հետո, որպեսզի համապատասխանեն այստեղ օգտագործվածներին, նրա հավասարումը կունենա հետևյալ տեքը.

Հ. 7: ${\displaystyle f_{r}=\gamma \left(1-\beta \cos \theta _{s}\right)f_{s}.}$

Տարբերությունները բխում են նրանից, որ Էյնշտեյնը գնահատել է ${\displaystyle \theta _{s}}$ անկյունը ոչ միայն դիտորդի, այլ նաև աղբյուրի հանգստի համակրգում։ ${\displaystyle \theta _{s}}$ հավասար չէ ${\displaystyle \theta _{r}}$ հարաբերական շեղման ազդեցության պատճառով։ Հարաբերական շեղման հավասարումը հետևյալն է.

Հ. 8: ${\displaystyle \cos \theta _{r}={\frac {\cos \theta _{s}-\beta }{1-\beta \cos \theta _{s}}}\,}$

Տեղադրելով հարաբերական շեղման 8-րդ հավասարումը 6-րդ հավասարման մեջ, ստացվում է հավասարում 7ը, որը ցույց է տալիս այս այլընտրանքային հավասարումների հետևողականությունը Դոպլերի տեղաշարժի համար^[10]։

Կարգավորում՝ ${\displaystyle \theta _{r}=0}$ 6-րդ կամ 7-րդ հավասարումների մեջ կստանանք Հավասարում 1-ը՝ հարաբերական երկայնական դոպլերային շեղման արտահայտությունը։

Այս արդյունքների ստացման չորս վեկտորային մոտեցումները հնարավոր է գտնել Լանդաուի և Լիֆշիթզի աշխատություններում (2005)^[11]։

Վիզուալիզացիա

Նկար 8. Ռելյատիվիստական Դոպլերի էֆեկտի համեմատությունը (վերևում) ոչ հարաբերական էֆեկտի հետ (ներքևում):

Նկ. 8-ն օգնում է մեզ որակական իմաստով հասկանալ, թե ինչպես են հարաբերական Դոպլերի էֆեկտը և ռելյատիվիստական շեղումը տարբերվում ոչ հարաբերական Դոպլերի էֆեկտից և լույսի ոչ հարաբերական շեղումից։ Ենթադրենք, որ դիտորդը բոլոր ուղղություններում շրջապատված է միատեսակ դեղին աստղերով, որոնք արձակում են 570 նմ մոնոխրոմատիկ լույս։ Դիագրամի Յուրաքանչյուր սլաք ներկայացնում է դիտորդի արագության վեկտորը շրջակա միջավայրի նկատմամբ՝ 0,89c մեծությամբ։

• Ռելյատիվիստական շեղման դեպքում դիտորդի առջև գտնվող լույսը կապույտ շեղումով տեղափոխվում է մինչև 137 նմ ալիքի երկարությամբ հեռավոր ուլտրամանուշակագույնում, մինչդեռ դիտորդի հետևում գտնվող լույսը կարմիր տեղաշարժվում է մինչև 2400 նմ ինֆրակարմիր ալիքի կարճ երկարությամբ։ Լույսի հարաբերական շեղման պատճառով առարկաները, որոնք նախկինում դիտորդի նկատմամբ ուղիղ անկյան տակ էին, 63°-ով առաջ թեքվել են։
• Ոչ հարաբերական շեղման դեպքում, դիտորդի առջևի լույսը միջին ուլտրամանուշակագույնում կապույտ շեղվումամբ փոխվում է մինչև 300 նմ ալիքի երկարություն, մինչդեռ դիտորդի ետևում գտնվող լույսը միջանկյալ ինֆրակարմիրում, կարմիր շեղմամբ տեղաշարժվում է մինչև 5200 նմ։ Լույսի շեղման պատճառով նախկինում դիտորդի նկատմամբ ուղիղ անկյան տակ գտնվող առարկաները 42°-ով շեղվել են։
• Երկու դեպքում էլ դիտորդի առջև ում և հետևում գտնվող մոնոխրոմատիկ աստղերը Դոպլերի Էֆֆեկտով շեղված են դեպի անտեսանելի ալիքների երկարություններ։ Այնուամենայնիվ, եթե դիտորդն ունենար աչքեր, որոնք կարողանային տեսնել ուլտրամանուշակագույն և ինֆրակարմիր ճառագայթները, ապա նա կտեսներ իր առջևի աստղերը ավելի պայծառ և ավելի սերտորեն հավաքված, քան ետևում գտնվող աստղերը, բայց աստղերը շատ ավելի պայծառ ու կենտրոնացած կլինեն հարաբերական Դոպլերի էֆֆեկտի դեպքում^[12]։

Իրականում աստղերը մոնոխրոմատիկ չեն, այլ արձակում են մի շարք տարբեր ալիքի երկարություններ, որոնք մոտ են սև մարմնի բաշխմանը։ Միանշանակ ճիշտ չէ, որ դիտորդի դիմաց գտնվող աստղերը ավելի կապույտ են երևում։ Դա ավելի շատ պայմանավորված է նրանով, որ ամբողջ սպեկտրային էներգիայի բաշխումը շեղվում է։ Միևնույն ժամանակ, երբ տեսանելի լույսը փոխվում է կապույտ անտեսանելի ուլտրամանուշակագույն ալիքի երկարությունների, ինֆրակարմիր ճառագայթը շեղվում է դեպի տեսանելի տիրույթ։ Գույների հստակ փոփոխությունները կախված են մարդու աչքի ֆիզիոլոգիայից և դիտարկվող լույսի աղբյուրների սպեկտրալ բնութագրերից^[13][14]։

Դոպլերի Էֆֆեկտի ազդեցությունը ինտենսիվության վրա

Դոպլերի էֆեկտը (կամայական ուղղությամբ) նաև փոփոխում է աղբյուրի կողմից ընկալվող լույսի ինտենսիվությունը. սա կարելի է հակիրճ արտահայտել նրանով, որ եթե աղբյուրի ուժը բաժանենք հաճախականության խորանարդի վրա, ապա Լորենցի գործոնը կմնա անփոփոխ^{[p 6][Ն 1]}։ Սա ենթադրում է, որ ընդհանուր ճառագայթման ինտենսիվությունը (բոլոր հաճախականությունների վրա ազդող) բազմապատկվում է հաճախականության համար նախատեսված Դոպլերի գործոնի չորրորդ հզորությամբ։

Որպես հետևանք. Պլանկի օրենքը նկարագրում է սև մարմնի ճառագայթումը, որպես համաչափ հաճախականությամբ սպեկտրային ինտենսիվություն. ${\displaystyle \nu ^{3}/\left(e^{h\nu /kT}-1\right)}$ բանաձևով (որտեղ T- ն աղբյուրի ջերմաստիճանն է և ν-ն հաճախականությունը)։ Այստեղից կարող ենք եզրակացնել, որ սև մարմնի սպեկտրը, որը դիտվում է Դոպլերի շեղման ժամանակ (կամայական ուղղվածությամբ) դեռևս սև մարմնի սպեկտր է, որի ջերմաստիճանը բազմապատկվում է նույն Դոպլերի գործակցով, ինչպես հաճախության ժամանակ։

Այս արդյունքը ցույց է տալիս ապացույցներից մեկը, որը օգնում է տարբերել Մեծ պայթյունի տեսությունը այլընտրանքային տեսություններից, որոնք նախատեսված են բացատրելու տիեզերական կարմիր շեղումը^[15]։

Փորձարարական ստուգում

Քանի որ լայնակի Դոպլերի էֆեկտը հարաբերականության հատուկ տեսության հիմնական նոր կանխատեսումներից մեկն է, փորձի հիմնական նպատակը եղել է էֆեկտի հայտնաբերումը և ճշգրիտ քանակականացումը հարաբերականության հատուկությունը հայտնաբերելու նպատակով։

Այվսի և Ստիլվելի չափումներ

Նկար 9. Ինչու է դժվար չափել լայնակի Դոպլերի էֆեկտը լայնակի ճառագայթի միջոցով:

Էյնշտեյնը (1907) ի սկզբանե առաջարկել էր, որ ԼԴԷ-ն կարող է չափվել՝ դիտելով ճառագայթի նկատմամբ ուղիղ անկյան տակ գտնվող «ջրանցքի ճառագայթները»^{[p 1]}։ Այս սխեմայով ԼԴԷ-ն չափելու փորձերն ձախողվեցին, քանի որ մասնիկների ճառագայթման առավելագույն արագությունը, որն առկա էր այն ժամանակ, կազմում էր լույսի արագության ընդամենը մի քանի հազարերորդական մասը։

Նկ. 9-ը ցույց է տալիս 4861-րդ Անգստրոմի գիծը չափելու փորձի արդյունքները, որոնք արտանետվում են ջրանցքի ճառագայթներից (H1+, H2+ և H3+ իոնների խառնուրդ) և վերամիավորվում են ջրանցքի ճառագայթային խողովակը լցնելու համար օգտագործվող նոսր ջրածնի գազից մաքրված էլեկտրոնների հետ։ Այստեղ, ԼԴԷ-ի կանխատեսված արդյունքը 4861.06 Անգստրոմ գիծ է։ Ձախ կողմում, երկայնական Դոպլերի շեղումը ընդլայնում է արտանետումների գիծն այնքան, որ ԼԴԷ-ն հնարավոր չի լինում դիտարկել։ Միջին մա ցույց են տալիս, որ նույնիսկ եթե մեկը նեղացնում է իր տեսադաշտը դեպի ճառագայթի ճշգրիտ կենտրոնը, ճառագայթի շատ փոքր շեղումները ճշգրիտ ուղիղ անկյան տակ առաջացնում են շեղումներ, որոնք համեմատելի են կանխատեսված ազդեցության հետ։

ԼԴԷ-ն հասարակ ձևով չափելու փոխարեն, Այվսը և Ստիլվելը (1938) օգտագործեցին գոգավոր հայելի, որը թույլ տվեց նրանց միաժամանակ դիտարկել գրեթե երկայնական ուղիղ ճառագայթը (կապույտ) և դրա արտացոլված պատկերը (կարմիր)։ Ինչի հետևանքով, սպեկտրոսկոպիկորեն դիտվեցին երեք գիծ՝ չտեղաշարժված արտանետման գիծ և կապույտ ու կարմիր շեղումների գծեր։ Կարմիր և կապույտ շեղված գծերի միջինը կհամեմատվի չտեղահանված արտանետման գծի ալիքի երկարության հետ։ Տարբերությունը, որը չափել են Այվսը և Ստիլվելը, փորձարարական սահմաններում համապատասխանում է հարաբերականության հատուկ տեսության կողմից կանխատեսված արդյունքին և էֆեկտին^{[p 7]}։

Այվսի և Սթիլվելի փորձերը հետագայում կրկնվեցին և որդեգրվեցին տարբեր ռազմավարություններ կապույտ և կարմիր շեղման ճառագայթային արտանետումների միջինը չափելու համար։ Վերջին շրջանում փորձի կրկնությունների ռամանակ օգտագործվել են ժամանակակից արագացուցիչ տեխնոլոգիաններ՝ երկու հակապտտվող մասնիկների ճառագայթները տեսանելի դարձնելու համար։ Փորձի հետագա կրկնություններում գամմա ճառագայթների էներգիաները, որոնք արձակվում են արագ շարժվող մասնիկների ճառագայթով, չափվել են մասնիկների ճառագայթի ուղղության նկատմամբ հակառակ անկյուններով։ Այս փորձերը իրականում չեն չափում մասնիկների ճառագայթային ալիքի երկարությունը դրա նկատմամբ ուղիղ անկյան տակ, ուստի որոշ գիտնականներ գերադասել են իրենց չափած էֆեկտն անվանել որպես «քառակուսի դոպլերի տեղաշարժ», այլ ոչ թե ԼԴԷ^{[p 8][p 9]}։

Դոպլերի լայնակի էֆեկտի ուղիղ չափումներ

Մասնիկների արագացուցիչ տեխնոլոգիայի հայտնվելը հնարավորություն տվեց զգալիորեն ավելի մեծ էներգիայի շնորհիվ մեծացնել մասնիկների ճառագայթների արտադրությունը, քան հասանելի էր Իվեսին և Սթիլվելլին։ Սա հնարավորություն է տվել նախագծել լայնակի Դոպլերի էֆեկտի փորձարկումները այնպես, ինչպես այն ի սկզբանե պատկերացրել էր Էյնշտեյնը, այսինքն՝ ուղղակիորեն դիտելով մասնիկների ճառագայթը 90° անկյան տակ։ Օրինակ, Հեսսելկափը (1979 թ.) Նկատել է, որ H ալֆա գիծը արտանետում է ջրածնի ատոմների սկսած 2.53 × 10 ⁸սմ/վ արագությունից մինչև 9,28×10 ⁸ սմ/վ արագություն, հարաբերական մոտավորմամբ երկրորդ կարգի անդամի գործակիցը գտնվելով 0,52±0,03 միջակայքում, գերազանց համաձայնեցվելով 1/2 տեսական արժեքների հետ^{[p 10]}։

Պտտվող հարթակների վրա ԼԴԷ-ի այլ ուղղակի փորձարկումները հնարավոր են դարձել Մյոսբաուերի էֆեկտի հայտնաբերման շնորհիվ, որը թույլ է տալիս արտադրել չափազանց նեղ ռեզոնանսային գծեր միջուկային գամմա ճառագայթների արտանետման և կլանման համար^[16]։ Մյոսբաուերի էֆեկտի փորձերը ապացուցել են, որ հեշտությամբ կարելի է հայտնաբերել ԵԴԷ-ն՝ օգտագործելով 2×10 ⁴ սմ/վ կարգի արտանետիչ-կլանիչ հարաբերական արագություն։ Այս փորձերը ներառում են Հեյ էթ ալի կողմից իրականացված փորձերը:

Ժամանակի դանդաղեցման չափումներ

Լայնակի Դոպլերի էֆեկտը և հարաբերականության հատուկ տեսության կինեմատիկական ժամանակի ընդլայնումը սերտորեն կապված են միմյանց հետ։ ԼԴԷ-ի բոլոր հաստատումները համընկնում են կինեմատիկական ժամանակի լայնացման մասին փաստարկների հետ նույնը և հակառակը։ Այսպիսով, հարց է առաջանում, թե «Ո՞րն է Հարաբերականության Հատուկ տեսության փորձարարական հիմքը»։ հակիրճ մեկնաբանությամբ փաստագրվել են բազմաթիվ թեստեր, որոնք տարիների ընթացքում օգտագործվել են հարաբերականության հատուկ տեսության տարբեր ասպեկտները հաստատելու կամ ժխտելու համար^[17]։ Kaivola et al. (1985)^{[p 11]} և McGowan et al. (1993)^{[p 12]} փորձերի օրինակներ են, որոնք ռեսուրսում դասակարգված են, որպես ժամանակի ընդլայնման փորձեր։ Այս երկուսը նաև ներկայացնում են ԼԴԷ-ի թեստեր։ Այս փորձերը համեմատում են երկու լազերի հաճախականությունը, որոնցից մեկը փակված է արագ ճառագայթող նեոնի ատոմի անցման հաճախությամբ, մյուսը՝ ջերմային նեոնում նույն անցման հաճախությամբ։ Փորձի 1993-ի տարբերակը ստուգեց ժամանակի ընդլայնումը, և, հետևաբար, ԼԴԷ-ն 2,3×10 ⁻⁶ ճշգրտությամբ։

Դոպլերի Հարաբերական էֆեկտը ձայնի և լույսի համար

Նկար 10. Դոպլերի Հարաբերական շեղման բանաձևը կիրառելի է ինչպես ձայնի, այնպես էլ լույսի համար:

Ֆիզիկայի առաջին տարվա դասագրքերը գրեթե նույն կերպով վերլուծում են ձայնի համար քննարկվող Դոպլերի շեղումը Նյուտոնյան կինեմատիկայի տեսանկյունից, մինչդեռ այն հիմնականում վերլուծվում է լույսի և էլեկտրամագնիսական երևույթների տեսանկյունից հարաբերական կինեմատիկայում։ Ինչը թյուր տպավորություն է ստեղծում, որ ակուստիկ երևույթները պահանջում են այլ վերլուծություն, քան լույսը և ռադիոալիքները։

Ձայնի համար նախատեսված Դոպլերի էֆեկտի ավանդական վերլուծությունը ներկայացնում է ցածր արագության մոտարկումների ճշգրտում և հարաբերական վերլուծություն։ Ձայնի լրիվ հարաբերական վերլուծությունը, փաստորեն, հավասարապես կիրառելի է ինչպես ձայնային, այնպես էլ էլեկտրամագնիսական երևույթների համար։

Դիտարկենք Ժամանակի կախումը տարածությունից արտահայտող գրաֆիկը Նկ.10-ում։ Կարգավորման պատառաքաղի (աղբյուր) և ընդունիչի գծերից երկուսն էլ պատկերված են այս գծապատկերում։ Իրադարձությունները O -ն և A-ն ներկայացնում են կարգավորիչի երկու թրթռումները։ Պատառաքաղի տատանման պարբերությունը OA- ի մեծությունն է, իսկ AB- ի հակադարձ թեքությունը ներկայացնում է ազդանշանի տարածման արագությունը (այսինքն՝ ձայնի արագությունը) դեպի B դիտորդ։ Այսպիսով, մենք կարող ենք գրել^[10]

${\displaystyle c_{s}={\frac {x_{B}-x_{A}}{t_{B}-t_{A}}}}$ (speed of sound)

${\displaystyle v_{s}=-{\frac {x_{A}}{t_{A}}}}$        ${\displaystyle v_{r}={\frac {x_{B}}{t_{B}}}}$      (speeds of source and receiver)

${\displaystyle |OA|={\sqrt {t_{A}^{2}-(x_{A}/c)^{2}}}}$

${\displaystyle |OB|={\sqrt {t_{B}^{2}-(x_{B}/c)^{2}}}}$

ենթադրվում է, որ ${\displaystyle v_{s}}$${\displaystyle v_{r}}$ ավելի փոքր են c${\displaystyle c_{s}}$-ից, քանի որ հակառակ դեպքում դրանց միջով հարվածային ալիքների անցնելու երևությը կառաջացնի սխալ հաշվարկը։ Որոշ սովորական հանրահաշիվ տալիս է հաճախականությունների հարաբերակցությունը.

Eq. 9:    ${\displaystyle {\frac {f_{r}}{f_{s}}}={\frac {|OA|}{|OB|}}}$ ${\displaystyle ={\frac {1-v_{r}/c_{s}}{1+v_{s}/c_{s}}}{\sqrt {\frac {1-(v_{s}/c)^{2}}{1-(v_{r}/c)^{2}}}}}$

${\displaystyle v_{r}}$ և ${\displaystyle v_{s}}$ արագությունները համեմատաբար փոքր են ${\displaystyle c}$-ից, որի հետևանքով վերը նշված հավասարումը վերածվում է ձայնի համար նախատեսված դասական Դոպլերի բանաձևի։

Նկար 11. Աղբյուրը և ստացողը շարժվում են տարբեր ուղղություններով և արագություններով այնպիսի շրջանակում, որտեղ ձայնի արագությունը անկախ է ուղղությունից:

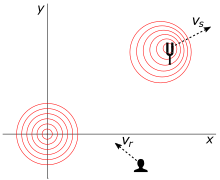
Նկ.11-ը պատկերում է երկու հարթության դեպք։ Աղբյուրը շարժվում է ${\displaystyle \mathbf {v_{s}} }$արագությամբ (արտանետման պահին)։ Այն արձակում է ազդանշան, որը ${\displaystyle \mathbf {C} }$ արագությամբ շարժվում է դեպի ընդունիչ,որը ազդակի ընդունման ժամանակ սկսում է շարժվել ${\displaystyle \mathbf {v_{r}} }$արագությամբ։ Վերժնական վերլուծությունը կատարվում է կոորդինատային համակարգում, որտեղ ազդանշանի ${\displaystyle |\mathbf {C} |}$ արագությունը ուղղությունից անկախ է^[6]։

Աղբյուրի և դիտորդի համապատասխան հաճախականությունների հարաբեությունը հետևյալն է.

Eq. 10:    ${\displaystyle {\frac {f_{r}}{f_{s}}}={\frac {1-{\frac {|\mathbf {v_{r}} |}{\mathbf {|C|} }}\cos(\theta _{\mathbf {C,v_{r}} })}{1-{\frac {|\mathbf {v_{s}} |}{\mathbf {|C|} }}\cos(\theta _{\mathbf {C,v_{s}} })}}{\sqrt {\frac {1-(v_{s}/c)^{2}}{1-(v_{r}/c)^{2}}}}}$

Առաջատար հարաբերությունն ունի դասական Դոպլերի էֆեկտի բանաձևի տեսքը, սակայն քառակուսի արմատը ներկայացնում է հարաբերական ուղղումը։ Եթե դիտարկենք աղբյուրի հետ կապված անկյունները և ${\displaystyle v_{s}=0}$-ն, ապա 10-րդ հավասարումը վերածվում է 7-րդ հավասարմանը՝ 1905 թ.-ին Էյնշտեյնի Դոպլերի էֆեկտի բանաձևին։ Իսկ եթե հաշվի առնենք դիտորդի շրջանակի հետ կապված անկյունները և ${\displaystyle v_{r}=0}$-ն, ապա 10-րդ հավասարումը վերածվում է 6-րդ հավասարմանը՝ նախկինում քննարկված Դոպլերի շեղմանհավասարման այլընտրանքային ձևին^[6]։

Տես նաև

• Դոպլերի էֆեկտ
• Դոպլերի ճառագայթում
• Կարմիր շեղում
• Կապույտ շեղում
• Ժամանակի դանդաղում
• Գրավիտացիոն ժամանակի դանդաղում
• Հարաբերականության հատուկ տեսություն

Նշումներ

1. Here, "source strength" refers to spectral intensity in frequency, i.e., power per unit solid angle and per unit frequency, expressed in watts per steradian per hertz; for spectral intensity in wavelength, the cube should be replaced by a fifth power.

Առաջնային աղբյուրներ

1. Einstein, Albert (1907). «On the Possibility of a New Test of the Relativity Principle (Über die Möglichkeit einer neuen Prüfung des Relativitätsprinzips)». Annalen der Physik. 328 (6): 197–198. Bibcode:1907AnP...328..197E. doi:10.1002/andp.19073280613.
2. Einstein, Albert (1905). «Zur Elektrodynamik bewegter Körper». Annalen der Physik (գերմաներեն). 322 (10): 891–921. Bibcode:1905AnP...322..891E. doi:10.1002/andp.19053221004. English translation: ‘On the Electrodynamics of Moving Bodies’
3. Kündig, Walter (1963). «Measurement of the Transverse Doppler Effect in an Accelerated System». Physical Review. 129 (6): 2371–2375. Bibcode:1963PhRv..129.2371K. doi:10.1103/PhysRev.129.2371.
4. Champeney, D. C.; Moon, P. B. (1961). «Absence of Doppler Shift for Gamma Ray Source and Detector on Same Circular Orbit». Proc. Phys. Soc. 77 (2): 350–352. Bibcode:1961PPS....77..350C. doi:10.1088/0370-1328/77/2/318.
5. Synge, J. L. (1963). «Group Motions in Space-time and Doppler Effects». Nature. 198 (4881): 679. Bibcode:1963Natur.198..679S. doi:10.1038/198679a0.
6. Johnson, Montgomery H.; Teller, Edward (1982 թ․ փետրվար). «Intensity changes in the Doppler effect». Proc. Natl. Acad. Sci. USA. 79 (4): 1340. Bibcode:1982PNAS...79.1340J. doi:10.1073/pnas.79.4.1340. PMC 345964. PMID 16593162.
7. Ives, H. E.; Stilwell, G. R. (1938). «An experimental study of the rate of a moving atomic clock». Journal of the Optical Society of America. 28 (7): 215. Bibcode:1938JOSA...28..215I. doi:10.1364/JOSA.28.000215.
8. Olin, A.; Alexander, T. K.; Häusser, O.; McDonald, A. B.; Ewan, G. T. (1973). «Measurement of the Relativistic Doppler Effect Using 8.6-MeV Capture γ Rays». Phys. Rev. D. 8 (6): 1633–1639. Bibcode:1973PhRvD...8.1633O. doi:10.1103/PhysRevD.8.1633.
9. Mandelberg, Hirsch I.; Witten, Louis (1962). «Experimental Verification of the Relativistic Doppler Effect». Journal of the Optical Society of America. 52 (5): 529–535. Bibcode:1962JOSA...52..529M. doi:10.1364/JOSA.52.000529.
10. Hasselkamp, D.; Mondry, E.; Sharmann, A. (1979). «Direct observation of the transversal Doppler-shift». Zeitschrift für Physik A. 289 (2): 151–155. Bibcode:1979ZPhyA.289..151H. doi:10.1007/BF01435932.
11. Kaivola, Matti; Riis, Erling; Lee, Siu Au (1985). «Measurement of the Relativistic Doppler Shift in Neon» (PDF). Phys. Rev. Lett. 54 (4): 255–258. Bibcode:1985PhRvL..54..255K. doi:10.1103/PhysRevLett.54.255. PMID 10031461.
12. McGowan, Roger W.; Giltner, David M.; Sternberg, Scott J.; Lee, Siu Au (1993). «New measurement of the relativistic Doppler shift in neon». Phys. Rev. Lett. 70 (3): 251–254. Bibcode:1993PhRvL..70..251M. doi:10.1103/PhysRevLett.70.251. PMID 10054065.

Ծանոթագրություններ

1. Sher, D. (1968). «The Relativistic Doppler Effect». Journal of the Royal Astronomical Society of Canada. 62: 105–111. Վերցված է 2018 թ․ հոկտեմբերի 11-ին.
2. Gill, T. P. (1965). The Doppler Effect. London: Logos Press Limited. էջեր 6–9. OL 5947329M.
3. Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (1977 թ․ փետրվար). «Relativistic Effects in Radiation». The Feynman Lectures on Physics: Volume 1. Reading, Massachusetts: Addison-Wesley. էջեր 34–7 f. ISBN 9780201021165. LCCN 2010938208.
4. Morin, David (2008). «Chapter 11: Relativity (Kinematics)» (PDF). Introduction to Classical Mechanics: With Problems and Solutions. Cambridge University Press. էջեր 539–543. ISBN 978-1-139-46837-4. Արխիվացված է օրիգինալից (PDF) 2018 թ․ ապրիլի 4-ին.
5. In his seminal paper of 1905 introducing special relativity, Einstein had already published an expression for the Doppler shift perceived by an observer moving at an arbitrary angle with respect to an infinitely distant source of light. Einstein's 1907 derivation of the TDE represented a trivial consequence of his earlier published general expression.^{[p 2]}
6. Brown, Kevin S. «The Doppler Effect». Mathpages. Վերցված է 2018 թ․ հոկտեմբերի 12-ին.
7. Misner, C. W., Thorne, K. S., and Wheeler, J. A (1973). Gravitation. Freeman. էջ 163. ISBN 978-0716703440.
8. Sama, Nicholas (1969). «Some Comments on a Relativistic Frequency-Shift Experiment of Champeney and Moon». American Journal of Physics. 37 (8): 832–833. Bibcode:1969AmJPh..37..832S. doi:10.1119/1.1975859.
9. Keswani, G. H. (1965). Origin and Concept of Relativity. Delhi, India: Alekh Prakashan. էջեր 60–61. Վերցված է 2018 թ․ հոկտեմբերի 13-ին.
10. Brown, Kevin S. «Doppler Shift for Sound and Light». Mathpages. Վերցված է 2015 թ․ օգոստոսի 6-ին.
11. Landau, L.D.; Lifshitz, E.M. (2005). The Classical Theory of Fields. Course of Theoretical Physics: Volume 2. Trans. Morton Hamermesh (Fourth revised English ed.). Elsevier Butterworth-Heinemann. էջեր 116–117. ISBN 9780750627689.
12. Savage, C. M.; Searle, A. C. (1999). «Visualizing Special Relativity» (PDF). The Physicist. 36 (141). Արխիվացված է օրիգինալից (PDF) 2008 թ․ օգոստոսի 3-ին. Վերցված է 2018 թ․ հոկտեմբերի 17-ին.
13. Brandeker, Alexis. «What would a relativistic interstellar traveller see?». Physics FAQ. Math Department, University of California, Riverside. Արխիվացված է օրիգինալից 2021 թ․ մայիսի 7-ին. Վերցված է 2018 թ․ հոկտեմբերի 17-ին.
14. Kraus, U. (2000). «Brightness and color of rapidly moving objects: The visual appearance of a large sphere revisited» (PDF). Am. J. Phys. 68 (1): 56–60. Bibcode:2000AmJPh..68...56K. doi:10.1119/1.19373. Վերցված է 2018 թ․ հոկտեմբերի 17-ին.
15. Wright, Edward L. ("Ned"). «Errors in Tired Light Cosmology». Ned Wright's Cosmology Tutorial. Astronomy Department, University of California, Los Angeles. Վերցված է 2018 թ․ հոկտեմբերի 17-ին.
16. Saburo Nasu (2013). «General Introduction to Mössbauer Spectroscopy». In Yoshida, Yutaka; Langouche, Guido (eds.). Mössbauer Spectroscopy: Tutorial Book. Springer. էջեր 1–22. ISBN 978-3642322198.
17. Roberts, Tom; Schleif, Siegmar. «What is the experimental basis of Special Relativity?». The Original Usenet Physics FAQ. Department of Mathematics, University of California, Riverside. Վերցված է 2018 թ․ հոկտեմբերի 16-ին.

Հետագա ընթերցում

• Moriconi, M (2006 թ․ նոյեմբերի 1). «Special theory of relativity through the Doppler effect». European Journal of Physics. 27 (6): 1409–1423. arXiv:physics/0605204. Bibcode:2006EJPh...27.1409M. doi:10.1088/0143-0807/27/6/015.

Արտաքին հղումներ

• Warp Special Relativity Simulator Համակարգչային ծրագիր, որը ցուցադրում է հարաբերական Դոպլերի էֆեկտը։
• Kraus, Ute; Zahn, Corvin. «Space Time Travel: Visualization of the theory of relativity». SpacetimeTravel.org. Physics and Astronomy Education Group, Hildesheim University, Germany. Վերցված է 2018 թ․ հոկտեմբերի 17-ին.