Distribuzione di Gumbel

Distribuzione di Gumbel
Funzione di densità di probabilità
Funzione di ripartizione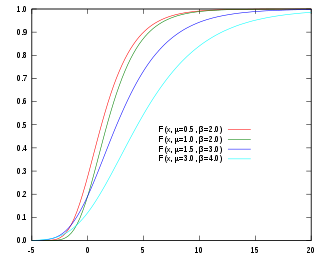
Parametri	${\displaystyle u\ }$ ${\displaystyle \beta >0\ }$
Supporto	${\displaystyle x\in (-\infty ;+\infty )}$
Funzione di densità	${\displaystyle {\frac {1}{\beta }}e^{-z-e^{-z}}}$ dove ${\displaystyle z={\frac {x-u}{\beta }}}$
Funzione di ripartizione	${\displaystyle \exp(-e^{-z})}$
Valore atteso	${\displaystyle u+\beta \,\gamma }$
Mediana	${\displaystyle u-\beta \,\ln(\ln(2))}$
Moda	${\displaystyle u}$
Varianza	${\displaystyle {\frac {\pi ^{2}}{6}}\,\beta ^{2}}$
Indice di asimmetria	${\displaystyle {\frac {12{\sqrt {6}}\,\zeta (3)}{\pi ^{3}}}\approx 1,14}$
Curtosi	${\displaystyle {\frac {12}{5}}}$
Entropia	${\displaystyle \ln(\beta )+\gamma +1}$
Funzione generatrice dei momenti	${\displaystyle \Gamma (1-\beta \,t)\,e^{u\,t}}$
Funzione caratteristica	${\displaystyle \Gamma (1-i\,\beta \,t)\,e^{i\,u\,t}}$

In teoria delle probabilità, la distribuzione di Gumbel o distribuzione del valore estremo di primo tipo, dall'inglese Extreme Value type 1 (EV1),^[1] è una distribuzione di probabilità continua a due parametri ${\displaystyle \alpha }$ e ${\displaystyle u}$ che viene usata per descrivere i valori estremi di una serie stocastica continua; il suo nome deriva dal fatto che fu sviluppata ed applicata ai valori estremi da Emil Julius Gumbel.^[2]

La funzione di densità di probabilità è data da:^[1]

${\displaystyle p(x)=\alpha \cdot \exp(\alpha \cdot (u-x)-\exp(\alpha \cdot (u-x)))}$

dove:

• ${\displaystyle \alpha ={\frac {1,283}{\sigma (x)}}}$, essendo 1,283 lo scarto quadratico medio della variabile ridotta, mentre ${\displaystyle \sigma (x)}$ è lo scarto quadratico medio del campione di dati;
• ${\displaystyle u=\mu (x)-0,45\cdot \sigma (x)}$, essendo ${\displaystyle \mu (x)}$ la media del campione di dati.

o, equivalentemente, definendo:

• ${\displaystyle \beta ={{1} \over \alpha }}$ ;
• ${\displaystyle z={\frac {x-u}{\beta }}}$;

si ha la forma più compatta:

${\displaystyle p(z)={\frac {1}{\beta }}\cdot \exp(-z-\exp(-z))}$

La funzione di ripartizione è data da:^[1]

${\displaystyle P(x)=\exp(-\exp(\alpha \cdot (u-x)))}$

Applicazioni notevoli di questa distribuzione sono le previsioni di eventi di piena o di siccità in idrologia o le previsioni di terremoti devastanti in geostatistica.

Note

1. Università degli studi di Bergamo, Distribuzioni di probabilità per i valori estremi (PDF). URL consultato il 2 novembre 2021 (archiviato dall'url originale il 2 novembre 2021).
2. Gumbel, Emil Julius Gumbel, hydraulics, hydrology, Victor Miguel Ponce, su ponce.sdsu.edu. URL consultato il 6 gennaio 2022.

Voci correlate

• Distribuzione generalizzata dei valori estremi
• Distribuzione di Fréchet
• Distribuzione di Weibull
• Curva di possibilità climatica

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su Distribuzione di Gumbel

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica