Formazione a sciame

La formazione a sciame o lo sciamare, è un comportamento collettivo esibito da entità, in particolare animali, di dimensioni simili che si aggregano insieme, muovendosi pressappoco o nello stesso punto o in massa o migrando in una direzione. È un argomento altamente interdisciplinare.[1] Il termine sciamare o brulicare viene applicato in particolare agli insetti, ma può anche essere applicato a qualsiasi altra entità o animale che presenti un comportamento simile. Il termine floccaggio o mormorio può riferirsi in modo specifico allo sciamare negli uccelli, al radunarsi in gregge in riferimento alla sciamatura nei tetrapodi e all'aggregazione in banchi per indicare lo sciamare nei pesci. Anche il fitoplancton si riunisce in enormi sciami chiamati fioriture, anche se questi organismi sono alghe e non sono semoventi come gli animali. Per estensione, il termine "sciame" viene applicato anche alle entità inanimate che presentano comportamenti paralleli, come in uno sciame di robot, uno sciame di terremoti o uno sciame di stelle.
Da un punto di vista più astratto, la formazione a sciame è il movimento collettivo di un gran numero di entità semoventi.[2] Dal punto di vista di chi crea modelli matematici, si tratta di un comportamento emergente derivante da semplici regole che sono seguite dagli individui e non comporta alcun coordinamento centrale. La formazione a sciame è anche studiata dai fisici della materia attiva come fenomeno che non è in equilibrio termodinamico, e come tale richiede lo sviluppo di strumenti ulteriori a quelli disponibili dalla fisica statistica dei sistemi in equilibrio termodinamico.
La formazione a sciame è stata simulata per la prima volta su un computer nel 1986 con il software di simulazione Boids.[3] Questo software simula agenti semplici (boids) che possono spostarsi secondo una serie di regole base. Il modello è stato originariamente progettato per imitare il comportamento dello stormo degli uccelli, ma può essere applicato anche al branco dei pesci e ad altre entità che sciamano.
Modelli
[modifica | modifica wikitesto]Negli ultimi decenni, gli scienziati hanno iniziato a creare modelli sulla formazione a sciame per ottenere una comprensione più profonda del comportamento.
Modelli matematici
[modifica | modifica wikitesto]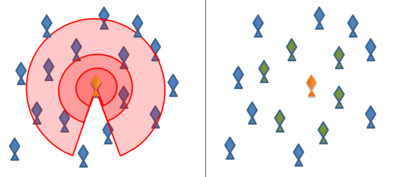
I primi studi sulla formazione a sciame impiegava modelli matematici per simulare e comprendere il comportamento. I modelli matematici più semplici di aggregazioni di animali in genere rappresentano singoli animali che seguono queste tre regole:
- Si muovono nella stessa direzione dei loro vicini
- Rimangono vicino ai loro vicini
- Evitano scontri con i loro vicini
Il programma per computer boids, creato da Craig Reynolds nel 1986, simula la formazione a sciame seguendo le regole di cui sopra.[3] Molti modelli successivi e attuali usano alcune variazioni di queste regole, spesso implementandole per mezzo di "zone" concentriche attorno a ciascun animale. Nella "zona di repulsione", molto vicina all'animale, l'animale focale cercherà di distanziarsi dai suoi vicini per evitare lo scontro. Leggermente più lontano, nella "zona di allineamento", l'animale focale cercherà di allineare la sua direzione di movimento con quella dei suoi vicini. Nella "zona di attrazione" più esterna, che si estende dall'animale focale tanto lontano quanto esso è in grado di percepire, l'animale focale cercherà di spostarsi verso un animale vicino.
La forma di queste zone sarà necessariamente influenzata dalle capacità sensoriali di un determinato animale. Ad esempio, il campo visivo di un uccello non si estende dietro il suo corpo. I pesci si affidano sia alla visione che alle percezioni idrodinamiche trasmesse attraverso le loro linee laterali, mentre il krill antartico si basa sia sulla visione che sui segnali idrodinamici trasmessi attraverso le antenne.
Tuttavia, recenti studi sugli stormi di storni hanno dimostrato che ogni uccello modifica la sua posizione, rispetto ai sei o sette animali che lo circondano, non importa quanto vicini o lontani siano quegli animali.[4] Le interazioni tra storni che si muovono in stormi si basano quindi su una regola topologica, piuttosto che metrica. Resta da vedere se questo vale per altri animali. Un altro recente studio, basato su un'analisi delle riprese ad alta velocità di stormi sopra Roma e che ipotizza regole comportamentali minime, ha simulato in modo convincente una serie di aspetti del comportamento dello stormo.[5][6][7][8]
Modelli evolutivi
[modifica | modifica wikitesto]Al fine di comprendere meglio perché gli animali sviluppano comportamenti brulicanti, gli scienziati si sono rivolti a modelli evolutivi che simulano popolazioni di animali in evoluzione. Tipicamente questi studi usano un algoritmo genetico per simulare l'evoluzione nel corso di molte generazioni. Questi studi hanno esaminato una serie di ipotesi che tentano di spiegare perché gli animali sviluppano comportamenti brulicanti, come la teoria della mandria egoista,[9][10][11][12] l'effetto di confusione dei predatori,[13][14] l'effetto di diluizione,[15][16] e la teoria dei molteplici occhi.[17]
Agenti
[modifica | modifica wikitesto]- (EN) Robert Mach e Frank Schweitzer, Multi-Agent Model of Biological Swarming, in Advances In Artificial Life, collana Lecture Notes in Computer Science, vol. 2801, 2003, pp. 810-820, DOI:10.1007/978-3-540-39432-7_87, ISBN 978-3-540-20057-4.
Auto-organizzazione
[modifica | modifica wikitesto]
Comportamento emergente
[modifica | modifica wikitesto]Il concetto di comportamento emergente – le cui proprietà e funzioni trovate a livello gerarchico non sono presenti e sono irrilevanti ai livelli inferiori – è spesso un principio di base dietro i sistemi auto-organizzanti.[18] Un esempio di auto-organizzazione in biologia che porta ad emergere nel mondo naturale si trova nelle colonie di formiche. La regina non dà ordini diretti e non dice alle formiche cosa fare.[senza fonte] Invece, ogni formica reagisce agli stimoli sotto forma di profumi chimici provenienti dalle larve, altre formiche, intrusi, cibo e accumulo di rifiuti e lascia dietro di sé una scia chimica che, a sua volta, fornisce uno stimolo per le altre formiche. Qui ogni formica è un'unità autonoma che reagisce in base solo al suo ambiente locale e alle regole codificate geneticamente per la sua varietà. Nonostante la mancanza di un processo decisionale centralizzato, le colonie di formiche mostrano comportamenti complessi e sono state persino in grado mostrare la capacità di risolvere problemi geometrici. Ad esempio, le colonie trovano abitualmente la massima distanza da tutti gli ingressi delle colonie per eliminare i corpi morti.
Stigmergia
[modifica | modifica wikitesto]Un ulteriore concetto chiave nel campo dell'intelligenza dello sciame è la stigmergia.[19][20] La stigmergia è un meccanismo di coordinamento indiretto tra agenti o azioni. Il principio è che la traccia lasciata nell'ambiente da un'azione stimola la prestazione di un'azione successiva, da parte dello stesso agente o di un agente diverso. In questo modo, le azioni successive tendono a rafforzarsi a vicenda, portando alla nascita spontanea di attività coerenti, apparentemente sistematiche. La stigmergia è una forma di auto-organizzazione. Produce strutture complesse, apparentemente intelligenti, senza bisogno di alcuna pianificazione, controllo o comunicazione diretta tra gli agenti. In quanto tale, supporta una collaborazione efficiente tra agenti estremamente semplici, che mancano di memoria, intelligenza o persino consapevolezza reciproca.[20]
Intelligenza dello sciame
[modifica | modifica wikitesto]L'intelligenza dello sciame è il comportamento collettivo di sistemi decentralizzati, auto-organizzati, naturali o artificiali. Il concetto è impiegato nel lavoro sull'intelligenza artificiale. L'espressione è stata introdotta da Gerardo Beni e Jing Wang nel 1989, nel contesto dei sistemi robotici cellulari.[21]
I sistemi di intelligenza dello sciame sono in genere costituiti da una popolazione di agenti semplici come i boidi che interagiscono a livello locale tra loro e il loro ambiente. Gli agenti seguono regole molto semplici e, sebbene non esista una struttura di controllo centralizzata che imponga come si dovrebbero comportare i singoli agenti, a livello locale e in una certa misura casuale, le interazioni tra tali agenti portano all'emergere di un comportamento intelligente globale, sconosciuto ai singoli agenti.
La ricerca sull'intelligenza dello sciame è multidisciplinare. Può essere suddivisa in ricerca sullo sciame naturale studiando sistemi biologici e ricerca sullo sciame artificiale studiando artefatti umani. Esiste anche un flusso scientifico che tenta di modellare gli stessi sistemi di sciami e di comprenderne i meccanismi sottostanti, e un flusso di ingegneria focalizzato sull'applicazione delle intuizioni sviluppate dalla corrente scientifica per risolvere problemi pratici in altre aree.[22]
Algoritmi
[modifica | modifica wikitesto]Gli algoritmi dello sciame seguono un approccio lagrangiano o un approccio euleriano.[23] L'approccio euleriano identifica lo sciame come un campo, che lavora con la densità dello sciame e trae proprietà del campo medio. È un approccio idrodinamico e può essere utile per modellare la dinamica generale di grandi sciami.[24][25][26] Tuttavia, la maggior parte dei modelli funziona con l'approccio lagrangiano, che è un modello basato su agenti che segue i singoli agenti (punti o particelle) che compongono lo sciame. I singoli modelli di particelle possono seguire le informazioni sulla direzione e sulla spaziatura che si perdono nell'approccio euleriano.[23][27]
Ottimizzazione delle colonie di formiche
[modifica | modifica wikitesto]L'ottimizzazione delle colonie di formiche è un algoritmo ampiamente utilizzato che è stato ispirato dai comportamenti delle formiche ed è stato efficace nella risoluzione di problemi di ottimizzazione discreta legati allo sciame.[28] L'algoritmo è stato inizialmente proposto da Marco Dorigo nel 1992,[29][30] e da allora è stato diversificato per risolvere una più ampia classe di problemi numerici. Le specie che hanno più regine possono avere una regina che lascia il nido insieme ad alcuni lavoratori per fondare una colonia in un nuovo sito, un processo simile alla sciamatura delle api.[31][32]
- Le formiche sono comportamentalmente poco sofisticate; collettivamente svolgono compiti complessi. Hanno una sofisticata comunicazione basata sui segni altamente sviluppata.
- Le formiche comunicano usando i feromoni; vengono rilasciate tracce che possono essere seguite da altre formiche.
- Le formiche che hanno problemi di direzionamento rilasciano diversi feromoni usati per calcolare il percorso "più breve" dal punto di origine alla(e) destinazione(i).
- (EN) E. M. Rauch, M. M. Millonas e D. R. Chialvo, Pattern formation and functionality in swarm models, in Physics Letters A, vol. 207, n. 3-4, 1995, p. 185, Bibcode:1995PhLA..207..185R, DOI:10.1016/0375-9601(95)00624-c, arXiv:adap-org/9507003.
Particelle semoventi
[modifica | modifica wikitesto]Il concetto di particelle semoventi (SPP) è stato introdotto nel 1995 da Tamás Vicsek et al.[33] come caso speciale del modello boids introdotto nel 1986 da Reynolds.[3] Uno sciame di SPP è modellato mediante una raccolta di particelle che si muovono a velocità costante e rispondono a perturbazioni casuali adottando ogni volta l'incremento della direzione media del movimento delle altre particelle prossime alla loro zona (modello di Vicsek).[34]
Le simulazioni dimostrano che una idonea "regola del vicino più prossimo" alla fine si traduce in tutte le particelle che sciamano insieme o si muovono nella stessa direzione. Ciò si evince, anche se non esiste un coordinamento centralizzato e anche se le particelle adiacenti a ciascuna particella cambiano costantemente nel tempo.[33] I modelli di SPP prevedono che gli animali brulicanti condividano determinate proprietà a livello di gruppo, indipendentemente dal tipo di animali nello sciame.[35] I sistemi sciamanti danno origine a comportamenti emergenti che si verificano su scale molto diverse, alcune delle quali sono sia universali che robuste. È diventata impresa ardua tra i fisici teorici trovare modelli statistici minimi che catturino questi comportamenti.[36][37]
Ottimizzazione con sciami di particelle
[modifica | modifica wikitesto]L'ottimizzazione con sciami di particelle è un altro algoritmo ampiamente utilizzato per risolvere i problemi relativi agli sciami. È stato sviluppato nel 1995 da Kennedy ed Eberhart e mirava inizialmente a simulare il comportamento sociale e la coreografia degli stormi di uccelli e dei banchi di pesci.[38][39] L'algoritmo è stato semplificato ed è stato osservato che stava eseguendo l'ottimizzazione. Il sistema inizialmente genera una popolazione con soluzioni casuali. In seguito ricerca nello spazio problematico attraverso generazioni successive usando l'ottimizzazione stocastica per trovare le soluzioni migliori. Le soluzioni che trova vengono chiamate punti materiali o particelle. Ogni particella memorizza la sua posizione e la migliore soluzione che ha raggiunto fino a quel momento. L'ottimizzatore con sciami di particelle tiene traccia del miglior valore locale ottenuto a quel momento da qualsiasi particella nel vicinato locale. Le particelle rimanenti si muovono quindi attraverso lo spazio problematico seguendo la particella guida delle particelle ottimali. Ad ogni iterazione, l'ottimizzatore con sciami di particelle accelera ogni particella verso le sue posizioni ottimali secondo semplici regole matematiche. L'ottimizzazione con sciami di particelle è stata applicata in moltei settori. Ha pochi parametri da regolare e una versione che funziona bene per applicazioni specifiche può anche funzionare bene con piccole modifiche in una vasta gamma di applicazioni correlate.[40] Un libro di Kennedy ed Eberhart descrive alcuni aspetti filosofici delle applicazioni di ottimizzazione con sciami di particelle e dell'intelligenza degli sciami.[41] Poli ha effettuato un'ampia indagine sulle applicazioni.[42][43]
Altruismo
[modifica | modifica wikitesto]I ricercatori svizzeri hanno sviluppato un algoritmo basato sulla regola della selezione parentale di Hamilton. L'algoritmo mostra come l'altruismo in uno sciame di entità può, nel tempo, evolversi e determinare una formazione a sciame più efficace.[44][45]
Evoluzione degli sciamanti
[modifica | modifica wikitesto]Insetti
[modifica | modifica wikitesto]Formiche
[modifica | modifica wikitesto]Mosche
[modifica | modifica wikitesto]Api
[modifica | modifica wikitesto]Scarafaggi
[modifica | modifica wikitesto]Locuste
[modifica | modifica wikitesto]
Migrazione degli insetti
[modifica | modifica wikitesto]
Uccelli
[modifica | modifica wikitesto]Migrazione degli uccelli
[modifica | modifica wikitesto]Vita marina
[modifica | modifica wikitesto]Pesci
[modifica | modifica wikitesto]Migrazione dei pesci
[modifica | modifica wikitesto]Krill
[modifica | modifica wikitesto]Copepodi
[modifica | modifica wikitesto]Fioriture algali
[modifica | modifica wikitesto]Piante
[modifica | modifica wikitesto]Batteri
[modifica | modifica wikitesto]Mammiferi
[modifica | modifica wikitesto]

Persone
[modifica | modifica wikitesto]
Robotica
[modifica | modifica wikitesto]Militare
[modifica | modifica wikitesto]Galleria d'immagini
[modifica | modifica wikitesto]-
Uno sciame di aringhe migranti
-
Uno sciame di api
-
Le salpidi disposte in catene formano enormi sciami.
-
Le persone che sciamano attraverso un'uscita non si comportano sempre come un fluido.
-
Uno sciame di coccinelle
-
Uno sciame di robot
-
Uno sciame di stelle antiche
Miti
[modifica | modifica wikitesto]Note
[modifica | modifica wikitesto]- ^ Roland Bouffanais, Design and Control of Swarm Dynamics, collana SpringerBriefs in Complexity, Firstª ed., Springer, 2016, DOI:10.1007/978-981-287-751-2, ISBN 978-981-287-750-5.
- ^ (EN) O'Loan e Evans, Alternating steady state in one-dimensional flocking, in Journal of Physics A: Mathematical and General, vol. 32, n. 8, 1998, pp. L99-L105, Bibcode:1999JPhA...32L..99O, DOI:10.1088/0305-4470/32/8/002, arXiv:cond-mat/9811336.
- ^ a b c (EN) C. W. Reynolds, Flocks, herds and schools: A distributed behavioral model, in Computer Graphics, vol. 21, n. 4, 1987, pp. 25-34, DOI:10.1145/37401.37406, ISBN 978-0-89791-227-3.
- ^ (EN) Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study, in Proc. Natl. Acad. Sci. U.S.A., vol. 105, n. 4, 2008, pp. 1232-7, Bibcode:2008PNAS..105.1232B, DOI:10.1073/pnas.0711437105, PMID 18227508, arXiv:0709.1916.
- ^ (EN) Self-organized aerial displays of thousands of starlings: a model, in Behavioral Ecology, vol. 21, n. 6, 2010, pp. 1349-1359, DOI:10.1093/beheco/arq149.
- ^ (EN) Some causes of the variable shape of flocks of birds, in PLOS One, vol. 6, n. 8, 2011, p. e22479, Bibcode:2011PLoSO...622479H, DOI:10.1371/journal.pone.0022479, PMID 21829627.
- ^ (EN) Swarms and schools - Self organization and complex behaviour, su rug.nl.
- ^ (EN) Research at the Faculty of Science and Engineering, su rug.nl.
- ^ (EN) Critical Interplay Between Density-dependent Predation and Evolution of the Selfish Herd, in Proceedings of GECCO 2013, Gecco '13, 2013, pp. 247-254, DOI:10.1145/2463372.2463394, ISBN 9781450319638.
- ^ (EN) Evolving collective behavior in an artificial ecology, in Artificial Life, vol. 7, n. 2, 2001, pp. 191-209, DOI:10.1162/106454601753139005, PMID 11580880.
- ^ (EN) Simulated evolution of selfish herd behavior, in Journal of Theoretical Biology, vol. 234, n. 2, 2005, pp. 213-225, DOI:10.1016/j.jtbi.2004.11.035, PMID 15757680.
- ^ (EN) Evolving the selfish herd: emergence of distinct aggregating strategies in an individual-based model, in Proc Biol Sci, vol. 274, n. 1618, 2007, pp. 1637-1642, DOI:10.1098/rspb.2007.0306, PMID 17472913.
- ^ (EN) Predator confusion is sufficient to evolve swarming behaviour, in J. R. Soc. Interface, vol. 10, n. 85, 2013, p. 20130305, DOI:10.1098/rsif.2013.0305, PMID 23740485.
- ^ (EN) Simulating predator attacks on schools: Evolving composite tactics (PDF), in Ecological Modelling, vol. 304, 2015, pp. 22-33, DOI:10.1016/j.ecolmodel.2015.02.018.
- ^ (EN) Tosh CR, Which conditions promote negative density dependent selection on prey aggregations? (PDF), in Journal of Theoretical Biology, vol. 281, n. 1, 2011, pp. 24-30, DOI:10.1016/j.jtbi.2011.04.014, PMID 21540037.
- ^ (EN) Predatory Fish Select for Coordinated Collective Motion in Virtual Prey, in Science, vol. 337, n. 6099, 2012, pp. 1212-1215, Bibcode:2012Sci...337.1212I, DOI:10.1126/science.1218919, PMID 22903520.
- ^ (EN) Exploring the evolution of a trade-off between vigilance and foraging in group-living organisms, in Royal Society Open Science, vol. 2, n. 9, 2015, p. 150135, Bibcode:2015RSOS....250135O, DOI:10.1098/rsos.150135, PMID 26473039, arXiv:1408.1906.
- ^ (EN) Hierarchy of Life, su authorstream.com. URL consultato il 14 luglio 2020 (archiviato dall'url originale il 3 luglio 2016).
- ^ (EN) H. v D. Parunak, Making swarming happen, in Proceedings of Conference on Swarming and Network Enabled Command, Control, Communications, Computers, Intelligence, Surveillance and Reconnaissance (C4ISR), Virginia, USA, McLean, 3 gennaio 2003.
- ^ a b (EN) L. Marsh e C. Onof, Stigmergic epistemology, stigmergic cognition (PDF), in Cognitive Systems Research, vol. 9, n. 1, 2008, pp. 136-149, DOI:10.1016/j.cogsys.2007.06.009.
- ^ (EN) G. Beni e J. Wang, Swarm Intelligence in Cellular Robotic Systems, Proceed. NATO Advanced Workshop on Robots and Biological Systems, Tuscany, Italy, 26-30 Giugno 1989.
- ^ (EN) M. Dorigo e M. Birattari, Swarm intelligence, in Scholarpedia, vol. 2, n. 9, 2007, p. 1462, Bibcode:2007SchpJ...2.1462D, DOI:10.4249/scholarpedia.1462.
- ^ a b (EN) Minimal mechanisms for school formation in self-propelled particles (PDF), in Physica D: Nonlinear Phenomena, vol. 237, n. 5, 2007, pp. 699-720, Bibcode:2008PhyD..237..699L, DOI:10.1016/j.physd.2007.10.009.
- ^ (EN) J. Toner e Y. Tu, Long-range order in a two-dimensional xy model: how birds fly together, in Physical Revue Letters, vol. 75, n. 23, 1995, pp. 4326-4329.
- ^ (EN) Swarming patterns in a two-dimensional kinematic model for biological groups, in SIAM J Appl Math, vol. 65, n. 1, 2004, pp. 152-174, Bibcode:2004APS..MAR.t9004T, DOI:10.1137/S0036139903437424.
- ^ (EN) A nonlocal continuum model for biological aggregation, in Bull Math Biol, vol. 68, n. 7, 2006, pp. 1601-1623, DOI:10.1007/s11538-006-9088-6, PMID 16858662, arXiv:q-bio/0504001.
- ^ (EN) J. Carrillo, M. Fornasier e G. Toscani, Particle, kinetic, and hydrodynamic models of swarming (PDF), in Modeling and Simulation in Science, Engineering and Technology, vol. 3, 2010, pp. 297-336, DOI:10.1007/978-0-8176-4946-3_12, ISBN 978-0-8176-4945-6.
- ^ Ant colony optimization Retrieved, su iridia.ulb.ac.be. URL consultato il 15 dicembre 2010.
- ^ (EN) A. Colorni, M. Dorigo e V. Maniezzo, Distributed Optimization by Ant Colonies, actes de la première conférence européenne sur la vie artificielle, Paris, France, Elsevier Publishing, 1991, pp. 134-142.
- ^ (EN) M. Dorigo, Optimization, Learning and Natural Algorithms, in PhD thesis, Milano, Politecnico di Milano, 1992.
- ^ (EN) Hölldobler & Wilson (1990), pp. 143–179
- ^ (EN) M. Dorigo, G. Di Caro e L. M. Gamberella, Ant Algorithms for Discrete Optimization, Artificial Life, MIT Press, 1999.
- ^ a b (EN) Novel type of phase transition in a system of self-driven particles, in Physical Review Letters, vol. 75, n. 6, 1995, pp. 1226-1229, Bibcode:1995PhRvL..75.1226V, DOI:10.1103/PhysRevLett.75.1226, PMID 10060237, arXiv:cond-mat/0611743.
- ^ (EN) Collective behavior of interacting self-propelled particles, in Physica A, vol. 281, n. 1-4, 2006, pp. 17-29, Bibcode:2000PhyA..281...17C, DOI:10.1016/S0378-4371(00)00013-3, arXiv:cond-mat/0611742.
- ^ (EN) From disorder to order in marching locusts (PDF), in Science, vol. 312, n. 5778, 2006, pp. 1402-1406, Bibcode:2006Sci...312.1402B, DOI:10.1126/science.1125142, PMID 16741126. URL consultato il 13 aprile 2011 (archiviato dall'url originale il 29 settembre 2011).
- ^ (EN) Hydrodynamics and phases of flocks (PDF), in Annals of Physics, vol. 318, n. 1, 2005, pp. 170-244, Bibcode:2005AnPhy.318..170T, DOI:10.1016/j.aop.2005.04.011. URL consultato il 16 luglio 2020 (archiviato dall'url originale il 18 luglio 2011).
- ^ (EN) E. Bertin, Droz e G. Grégoire, Hydrodynamic equations for self-propelled particles: microscopic derivation and stability analysis, in J. Phys. A, vol. 42, n. 44, 2009, p. 445001, Bibcode:2009JPhA...42R5001B, DOI:10.1088/1751-8113/42/44/445001, arXiv:0907.4688.
- ^ (EN) J. Kennedy e R. Eberhart, Particle Swarm Optimization, in Proceedings of IEEE International Conference on Neural Networks, IV, 1995, pp. 1942-1948.
- ^ (EN) J. Kennedy, The particle swarm: social adaptation of knowledge, in Proceedings of IEEE International Conference on Evolutionary Computation, 1997, pp. 303-308.
- ^ (EN) X. Hu, Particle swarm optimization: Tutorial, su swarmintelligence.org. URL consultato il 15 dicembre 2010.
- ^ (EN) J. Kennedy e R. C. Eberhart, Swarm Intelligence, Morgan Kaufmann, 2001, ISBN 978-1-55860-595-4.
- ^ (EN) R. Poli, An analysis of publications on particle swarm optimisation applications (PDF), in Technical Report CSM-469, 2007. URL consultato il 16 luglio 2020 (archiviato dall'url originale il 16 luglio 2011).
- ^ (EN) R. Poli, Analysis of the publications on the applications of particle swarm optimisation (PDF), in Journal of Artificial Evolution and Applications, vol. 2008, 2008, pp. 1-10, DOI:10.1155/2008/685175.
- ^ Altruism helps swarming robots fly better, su genevalunch.com, 4 maggio 2011 (archiviato dall'url originale il 15 settembre 2012).
- ^ (EN) M. Waibel, D. Floreano e L. Keller, A quantitative test of Hamilton's rule for the evolution of altruism, in PLOS Biology, vol. 9, n. 5, 2011, p. 1000615, DOI:10.1371/journal.pbio.1000615, PMID 21559320.
Bibliografia
[modifica | modifica wikitesto]- Blum C e Merkle D (2008) Swarm intelligence: introduzione e applicazioni Springer. ISBN 978-3-540-74088-9 .
- Camazine S, Deneubourg JL, Franks NR, Sneyd J, Theraulaz G e Bonabeau E (2003) Auto-organizzazione nei sistemi biologici Princeton University Press. ISBN 978-0-691-11624-2 .
- Fisher L (2009) Lo sciame perfetto: la scienza della complessità nella vita quotidiana Libri base. ISBN 978-0-465-01884-0 .
- Kennedy JF, Kennedy J, Eberhart RC e Shi Y (2001) Swarm intelligence Morgan Kaufmann. ISBN 978-1-55860-595-4 .
- Krause, J (2005) Vivere in gruppi Oxford University Press. ISBN 978-0-19-850818-2
- Lim CP, Jain LC e Dehuri S (2009) Innovazioni in Swarm Intelligence Springer. ISBN 978-3-642-04224-9 .
- Miller, Peter (2010) The Smart Swarm: come la comprensione di greggi, scuole e colonie può renderci migliori nel comunicare, prendere decisioni e portare a termine le attività Penguin, ISBN 978-1-58333-390-7
- Nedjah N e Mourelle LdM (2006) Swarm sistemi intelligenti Springer. ISBN 978-3-540-33868-0 .
- Sumpter, David JT (2010) Comportamento animale collettivo Princeton University Press. ISBN 978-0-691-14843-4 .
- Collective motion, in Physics Reports, vol. 517, 3–4, 2012, pp. 71–140, Bibcode:2012PhR...517...71V, DOI:10.1016/j.physrep.2012.03.004, arXiv:1010.5017.
Voci correlate
[modifica | modifica wikitesto]Altri progetti
[modifica | modifica wikitesto] Wikimedia Commons contiene immagini o altri file su Formazione a sciame
Wikimedia Commons contiene immagini o altri file su Formazione a sciame
Collegamenti esterni
[modifica | modifica wikitesto]- Articolo del New York Times sulle indagini sullo sciame
- Dal Wolfram Demonstrations Project - richiede un lettore CDF (gratuito) :
| Controllo di autorità | LCCN (EN) sh2009002808 · J9U (EN, HE) 987007542815005171 |
|---|







