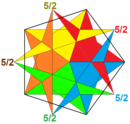
Piccolo dodecaedro stellato
| Piccolo dodecaedro stellato | |||
|---|---|---|---|
 | |||
| Tipo | Solido di Keplero-Poinsot | ||
| Forma facce | Pentagono stellato (pentagramma) | ||
| Nº facce | 12 | ||
| Nº spigoli | 30 | ||
| Nº vertici | 12 | ||
| Valenze vertici | 5 | ||
| Caratteristica di Eulero | -6 | ||
| Incidenza dei vertici | V(55)/2 | ||
| Notazione di Wythoff | 5 | 2 5⁄2 | ||
| Notazione di Schläfli | 5⁄2,5} | ||
| Diagramma di Coxeter-Dynkin |     
| ||
| Gruppo di simmetria | |||
| Duale | Grande dodecaedro | ||
| Proprietà | non chirale | ||
| Politopi correlati | |||
| |||
In geometria solida il piccolo dodecaedro stellato è uno dei quattro poliedri di Keplero-Poinsot. Lo si attribuisce comunemente a Keplero, anche se sono note rappresentazioni precedenti.[1]
Proprietà
[modifica | modifica wikitesto]Il piccolo dodecaedro stellato è un poliedro di Keplero-Poinsot: è cioè "regolare" ma non convesso. Le sue 12 facce sono poligoni stellati e si intersecano in più punti. I suoi vertici coincidono con quelli di un icosaedro.
Come tutti i poliedri regolari, il piccolo dodecaedro stellato ha tutte le facce regolari ed identiche, tutti gli spigoli della stessa lunghezza e lo stesso tipo di cuspide ad ogni vertice.
Lo stesso solido può essere interpretato con vertici, spigoli e facce diverse: è possibile infatti considerare "facce" soltanto i vari triangoli che stanno effettivamente sul bordo del poliedro. In questo caso si ottengono 60 facce, 90 spigoli e 32 vertici: da un punto di vista combinatorio, con questa descrizione il poliedro è un pentacisdodecaedro, in cui alcuni vertici sono stati però spostati verso l'esterno.
Nell'arte
[modifica | modifica wikitesto]
Il primo esempio di piccolo dodecaedro stellato nell'arte è raffigurato nel mosaico in uno degli ingressi della Basilica di San Marco a Venezia, realizzato da Paolo Uccello verso il 1430.[1]
La stessa figura è ripresa nelle due litrografie Contrast (Order and Chaos) (1950) e Gravitation (1952) di Escher.[2]
Poliedro duale
[modifica | modifica wikitesto]Il poliedro duale del piccolo dodecaedro stellato è il grande dodecaedro.
-
Piccolo dodecaedro stellato -
Trasparenza -
Modello -
Grafo
.jpg)
Note
[modifica | modifica wikitesto]- ^ a b Egidio Battistini, MatematicArchitettura, Esculapio, 2020, p. 38, ISBN 9791220205658.
- ^ John Barnes, Gems of Geometry, Springer, 2009, p. 56, ISBN 978-3-642-05092-3.
Bibliografia
[modifica | modifica wikitesto]- Henry Martin Cundy & A. P. Rollett, I modelli matematici, Milano, Feltrinelli, 1974.
- Maria Dedò, Forme, simmetria e topologia, Bologna, Decibel & Zanichelli, 1999, ISBN 88-08-09615-7.
- L. Berzolari, G. Vivanti, D. Gigli (a cura di), Enciclopedia delle Matematiche elementari, Milano, Ulrico Hoepli, 1979, ISBN 88-203-0265-9.
Altri progetti
[modifica | modifica wikitesto]
Wikimedia Commons contiene immagini o altri file sul piccolo dodecaedro stellato
Collegamenti esterni
[modifica | modifica wikitesto]- (EN) Eric W. Weisstein, Small Stellated Dodecahedron, su MathWorld, Wolfram Research.
