Precisione

Nella teoria degli errori, la precisione è il grado di "convergenza" (o "dispersione") di dati rilevati individualmente (campione) rispetto al valore medio della serie cui appartengono ovvero, in altri termini, la loro varianza (o deviazione standard) rispetto alla media campionaria.

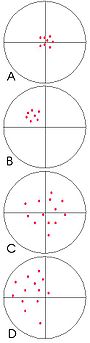
Facendo una analogia con una serie di frecce scagliate su un bersaglio, quanto più le frecce giungono raggruppate, tanto più la serie di tiri è precisa. Non importa quanto il centro del gruppo (la media) si avvicini al centro del bersaglio, quest'altro fattore è infatti determinato dall'accuratezza.
Nell'immagine a destra, le serie di dati A e B sono ugualmente precise, ma la serie B fornisce un valore medio scostato dal valore atteso, che è rappresentato dal centro del bersaglio: la misura è detta perciò inaccurata. In C, i dati sono poco precisi, ma la misura è invece accurata. In D, non si hanno né precisione né accuratezza.

La dispersione di valori può essere prodotta da variazioni casuali non ripetibili (errore statistico).
Per ottenere un valore medio affidabile è necessario effettuare un numero sufficientemente elevato di rilevazioni. In statistica la precisione è esprimibile in termini di deviazione standard.
Uno strumento preciso dovrebbe essere allo stesso tempo anche accurato, a meno di conoscere l'entità dello scostamento (errore sistematico) ed apportare le opportune correzioni.

Si distinguono tre diversi tipi di precisione:

  • ripetibilità: la dispersione di valori ottenuta usando gli stessi strumenti, con gli stessi operatori, nelle stesse condizioni ed in un tempo ragionevolmente breve,
  • riproducibilità: la dispersione ottenuta compiendo le stesse misurazioni con strumenti ed operatori differenti e/o su un tempo relativamente lungo.
  • precisione intermedia

Precisione degli strumenti di misura

[modifica | modifica wikitesto]

Nel campo degli strumenti di misura, la precisione è definita dal Vocabolario Internazionale di Metrologia (VIM)[1] come grado di concordanza tra indicazioni o valori misurati ottenuti da un certo numero di misurazioni ripetute dello stesso oggetto o di oggetti similari, eseguite in condizioni specificate.

Note

[modifica | modifica wikitesto]
  1. ^ VIM - International Vocabulary of Metrology, su ceinorme.it. URL consultato il 12 giugno 2020 (archiviato dall'url originale il 12 giugno 2020).

Voci correlate

[modifica | modifica wikitesto]

Altri progetti

[modifica | modifica wikitesto]

Collegamenti esterni

[modifica | modifica wikitesto]
  Portale Matematica
  Portale Metrologia
  Portale Scienza e tecnica