Viscoelasticità
La viscoelasticità è un modello matematico che descrive un materiale che si comporta in modo intermedio tra un solido elastico e un fluido. Costituisce un modello ampiamente studiato in reologia. Uno dei modelli più semplici di materiale viscoelastico è il fluido alla Boger, in cui la viscosità è costante.
L'individuazione del comportamento viscoelastico viene svolta misurando la variazione della viscosità η in funzione della velocità di deformazione . Nel caso di un fluido viscoelastico la viscosità dipende sia dalla temperatura che dalla velocità di deformazione, mentre per un fluido puramente viscoso la viscosità dipende esclusivamente dalla temperatura.
Storia
[modifica | modifica wikitesto]Nel XIX secolo, i fisici James Clerk Maxwell, Ludwig Boltzmann, Woldemar Voigt e William Thomson Kelvin studiarono i fenomeni di scorrimento viscoso (anche detto "creep") e recupero di vari materiali, tra cui: vetro, metalli e gomme.[1] Il modello della viscoelasticità fu ulteriormente elaborato alla fine del XX secolo in occasione della sintesi dei primi polimeri sintetici,[1] che manifestano comportamento viscoelastico.
Definizione
[modifica | modifica wikitesto]I materiali puramente viscosi rispondono ad una sollecitazione tangenziale manifestando un comportamento coerente con la legge di Newton, cioè originando al loro interno uno sforzo tangenziale pari al prodotto della velocità di deformazione e della viscosità; se sono invece sottoposti ad una sollecitazione normale non si oppongono in alcun modo.
I materiali elastici rispondono ad una sollecitazione normale manifestando un comportamento coerente con la legge di Hooke, cioè originando al loro interno uno sforzo normale pari al prodotto del modulo di Young e della deformazione (espressa in termini di allungamento percentuale) e ritornando al loro stato originario quando queste sollecitazioni cessano; se sono invece sottoposti ad una sollecitazione tangenziale non si oppongono in alcun modo.
I materiali viscoelastici si oppongono sia alle sollecitazioni tangenziali sia alle sollecitazioni normali, generando quindi al loro interno sia sforzi tangenziali sia sforzi normali.
Esempi di materiali viscoelastici
[modifica | modifica wikitesto]Sebbene alcuni materiali seguano abbastanza bene la legge di Newton oppure la legge di Hooke, tutti i materiali mostrano una deviazione più o meno marcata dal comportamento elastico e dal comportamento puramente viscoso, per cui dal punto di vista pratico tutti i materiali sono viscoelastici.
Di solito i metalli e le leghe (quali ad esempio l'acciaio o l'alluminio) e il quarzo (a temperatura ambiente e per piccole deformazioni) hanno un comportamento pressoché elastico. I polimeri sintetici, il legno, i tessuti umani e i metalli ad alta temperatura mostrano invece effetti viscoelastici significativi.
Alcuni esempi di materiali viscoelastici includono: polimeri amorfi, polimeri semicristallini, biopolimeri, metalli ad elevate temperature, e materiali bituminosi.
Comportamento reologico dei materiali viscoelastici
[modifica | modifica wikitesto]Nel caso dei materiali viscoelastici, la viscosità, intesa come costante di proporzionalità tra sforzo e velocità di deformazione, dipende dalla velocità di deformazione e quindi dal tempo.
La viscosità di un materiale viscoelastico è costituita da due contributi:
- la viscosità propriamente detta (in inglese shear viscosity), che è il rapporto tra gli sforzi tangenziali e la velocità di deformazione;
- la viscosità elongazionale (in inglese extensional viscosity o elongational viscosity), che è il rapporto tra gli sforzi normali e la velocità di deformazione.
Alcune proprietà dei materiali viscoelastici sono le seguenti:
- se lo sforzo si mantiene costante, la deformazione cresce con il tempo; tale fenomeno è detto "scorrimento viscoso" (o creep);
- se si mantiene costante la deformazione, lo sforzo decresce con il tempo; tale fenomeno è detto "rilassamento degli sforzi";
- la rigidità del materiale dipende dalla velocità di applicazione del carico;
- se viene applicato un carico ciclico, avviene un'isteresi (un ritardo periodico), con conseguente dissipazione (sotto forma di calore) di energia meccanica; rappresentando il ciclo di carico in un diagramma sforzo-deformazione, la perdita di energia meccanica è pari all'area del percorso che rappresenta il ciclo di carico;[2] tale perdita di energia meccanica non avviene invece nei materiali elastici, i quali riassumono la loro forma originaria una volta che il carico è rimosso;[2]
- le onde acustiche (così come quelle vibrazionali) subiscono un'attenuazione, a causa della dissipazione di energia dovuta all'isteresi dei cicli di carico-scarico;[non chiaro]
- la velocità di rimbalzo di un oggetto in seguito ad un urto con un materiale viscoelastico è inferiore alla velocità dell'oggetto prima dell'urto;
- durante il rotolamento di un materiale viscoelastico, gli effetti dell'attrito volvente sono accompagnati da effetti di attrito radente.
Modulo di rilassamento
[modifica | modifica wikitesto]Modulo dinamico
[modifica | modifica wikitesto]La viscoelasticità viene studiata usando l'analisi meccanica dinamica (DMA), applicando una piccola deformazione oscillatoria e misurando la tensione risultante.
A seconda della natura del materiale, si possono avere i seguenti casi:
- i materiali puramente elastici presentano sforzo e deformazione in fase, per cui la risposta al cambiamento di uno di questi parametri influenza in maniera immediata l'altro parametro;
- nei materiali puramente viscosi, la deformazione è ritardata rispetto allo sforzo di 90°.
- i materiali viscoelastici mostrano un comportamento intermedio tra il comportamento puramente elastico e quello puramente viscoso, mostrando un valore del ritardo della deformazione rispetto allo sforzo tra 0° e 90°.
Il modulo dinamico complesso G può essere usato per rappresentare le relazioni tra lo sforzo e la deformazione in una prova dinamica:
- G = G' + iG"
dove:
- ;
- rappresenta il contributo elastico, pari a:
- G" rappresenta il contributo viscoso, pari a:
- è l'ampiezza dello stress;
- è l'ampiezza della deformazione;
- è lo sfasamento tra stress e deformazione.
Viscoelasticità lineare e non lineare
[modifica | modifica wikitesto]La viscoelasticità lineare si ha quando la funzione è un'equazione differenziale ordinaria separabile nei confronti sia della risposta allo scorrimento viscoso sia del carico applicato. Tutti i modelli viscoelastici lineari possono essere rappresentati dall'equazione di Volterra, che lega lo sforzo e la deformazione:
oppure:
dove:
- t è il tempo;
- è lo sforzo;
- è la deformazione;
- è il modulo elastico istantaneo misurato nella prova di scorrimento viscoso;
- è il modulo elastico istantaneo misurato nella prova di rilassamento degli sforzi;
- K(t) è la funzione di scorrimento viscoso;
- F(t) è la funzione di rilassamento degli sforzi.
La viscoelasticità lineare di solito è applicabile solo nel caso di piccole deformazioni.
La viscoelasticità non lineare si ha quando la funzione non è separabile; in genere ciò accade quando le deformazioni sono grandi o se il materiale cambia le sue proprietà durante la deformazione.
Valutando il modulo elastico durante un esperimento di stress relaxation, si noterà un valore costante al variare della deformazione iniziale applicata nel caso in cui ci si trovi in regime di viscoelasticità lineare, viceversa nel caso in cui il regime fosse di viscoelasticità non lineare si otterrebbero diversi valori del modulo elastico al variare della deformazione iniziale; un analogo discorso può essere condotto nel caso in cui ad essere valutato fosse il modulo di compliance J(t) durante un esperimento di creep in regime di viscoelasticità lineare.
Equazioni costitutive dei materiali viscoelastici
[modifica | modifica wikitesto]Detti lo sforzo, è la deformazione, è il modulo elasticità di Young, il modulo di cedevolezza e il tempo.
Modelli a 2 elementi
[modifica | modifica wikitesto]Modello di Maxwell
[modifica | modifica wikitesto]Il modello di Maxwell descrive bene i materiali viscoelastici che si comportano in modo elastico su intervalli di tempo brevi e in modo viscoso su intervalli di tempo lunghi. In genere il modello di Maxwell viene impiegato per prevedere il comportamento dei materiali viscoelastici liquidi.

Tale modello è rappresentato da un dissipatore viscoso collegato in serie a una molla. Ad esso associata è la seguente equazione, che descrive il sistema sommando i due contributi:
in cui:
- è la deformazione legata al contributo viscoso
- è la deformazione legata al contributo elastico
Imponendo come condizioni al contorno:
si ottiene
- , dove
Modello di Kelvin-Voigt
[modifica | modifica wikitesto]In genere il modello di Kelvin-Voigt viene impiegato per prevedere il comportamento dei materiali viscoelastici solidi.

Tale modello è rappresentato da un dissipatore viscoso collegato in parallelo a una molla e l'equazione costitutiva ad esso associata è la seguente:
in cui:
- è lo sforzo legato al contributo elastico
- è lo sforzo legato al contributo viscoso
Imponendo come condizioni al contorno:
si ottiene
- , dove
Modelli a 3 elementi
[modifica | modifica wikitesto]Modello lineare standard di Zener
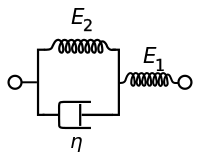
[modifica | modifica wikitesto]Il modello lineare standard, proposto per la prima volta da Clarence Zener, è un modello ideato per risolvere le problematiche dei modelli a due elementi. Può essere rappresentato da una molla collegata in parallelo ad un dissipatore viscoso e una molla collegati a loro volta in serie, secondo la rappresentazione di Maxwell, o da una molla in serie a un pistone e una molla posti in parallelo, secondo la rappresentazione di Kelvin-Voigt.
| Rappresentazione di Maxwell | Rappresentazione di Kelvin-Voigt |
|---|---|
 |
 |
Modello di Jeffreys-Lethersich
[modifica | modifica wikitesto]| Rappresentazione di Jeffreys | Rappresentazione di Lethersich |
|---|---|
 |
 |
Modello a 4 elementi di Alfrey-Burgers
[modifica | modifica wikitesto]Modelli Multi-elemento
[modifica | modifica wikitesto]Modello di Maxwell-Weichert
[modifica | modifica wikitesto]
Il modello di Maxwell-Weichert è rappresentato da una molla collegata in parallelo a più dissipatori viscosi e molle collegate a loro volta in serie. Il modello di Maxwell generalizzato è rappresentato da più elementi disposti in parallelo, ciascuno a sua volta costituito da una molla e da un dissipatore viscoso disposti in serie.
Modello di Kelvin-Voigt-Weichert
[modifica | modifica wikitesto]Il modello di Kelvin-Voigt generalizzato è rappresentato da più elementi disposti in serie, ciascuno a sua volta costituito da una molla e da un dissipatore viscoso disposti in parallelo.
Il modello di Kelvin-Voigt generalizzato coincide con il modello di Maxwell generalizzato nel caso in cui il numero di elementi tende ad infinito.
Rilassamento viscoelastico
[modifica | modifica wikitesto]In materiali come i polimeri termoplastici si osserva un rilassamento delle tensioni, detto anche rilassamento viscoelastico, portate a seguito di una certa deformazione imposta, il fenomeno si spiega con lo sgrovigliamento delle catene macromolecolari, sgrovigliamento che necessita di un certo tempo per compiersi.
Note
[modifica | modifica wikitesto]Bibliografia
[modifica | modifica wikitesto]- Silbey and Alberty (2001): Physical Chemistry, 857. John Wiley & Sons, Inc.
- Allen and Thomas (1999): "The Structure of Materials," 51.
- Crandal et al. (1999): "An Introduction to the Mechanics of Solids" 348
- J. Lemaitre and J.L. Chaboche (1994)" Mechanics of solid materials"
- (EN) William D. Callister, Material Science and Engineering: An Introduction, 5ª ed., John Wiley & Sons Inc, 1999, pp. 464-467, ISBN 0-471-35243-8.
Voci correlate
[modifica | modifica wikitesto]Altri progetti
[modifica | modifica wikitesto] Wikizionario contiene il lemma di dizionario «viscoelasticità»
Wikizionario contiene il lemma di dizionario «viscoelasticità» Wikimedia Commons contiene immagini o altri file sulla viscoelasticità
Wikimedia Commons contiene immagini o altri file sulla viscoelasticità
Collegamenti esterni
[modifica | modifica wikitesto]- (EN) viscoelasticity, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
| Controllo di autorità | NDL (EN, JA) 00568079 |
|---|





























![{\displaystyle \varepsilon (t)=C\sigma _{0}\left[1-\exp \left(-{\frac {t}{t_{rit}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b762e971f80ef6bd9f724352e273b2059c7a00b8)




