写像度

写像度（しゃぞうど、degree, mapping degree）とは、コンパクト、弧状連結、向き付けられた同次元の多様体間での連続写像を特徴付ける整数のこと。写像のホモトピー不変量のひとつである。

概要

円周 S¹上の連続写像 f : S¹ → S¹について、f の像が S¹を(向きを込めて)何重に被覆するかを考える。 例えば、 S¹ を絶対値 1 の複素数の集合（群）とみなしたとき、z を z^k にうつす写像は S ¹ を k 重に被覆する。 このように、写像 f が S¹ を k 重に被覆するとき、f の写像度が k である、という。 このとき、 f を連続変形しても写像度は変化しないことがわかる。

n 次元球面 Sⁿ上の連続写像 f : Sⁿ → Sⁿ や、もっと一般に n 次元多様体 M, N の間の連続写像 f : M → N についても同じように写像度を定義することができる。

定義

弧状連結で、向き付け可能な n 次元多様体 X の n 次ホモロジー群 H_n(X) は整数群 Z と同型であり、ひとつの生成元から生成される無限巡回群である。生成元となりうる元は ± の二つ存在するが、 X に向きを付けると、 どちらが + であるかを定める。 つまり、H_n(X) の生成元を定めることになる。この生成元を（向き付けられた）X の基本ホモロジー類といい、 [X] と書く。

コンパクト、弧状連結で向きのついたn 次元多様体 M, N と連続写像 f : M → N が与えられたとする。 f から誘導される準同型

${\displaystyle f_{*}:H_{n}(M)\rightarrow H_{n}(N)}$

について、

${\displaystyle ^{\exists 1}k\in \mathbb {Z} \ f_{*}([M])=k[N]}$

である。このとき、f の写像度 deg f を k で定義する。

なめらかな多様体の場合

M, N ともになめらかな多様体で 、f がなめらかな写像であった場合、 deg f を上の定義とは違う方法で計算できる。

M, N はコンパクトな多様体であるので、 任意の f の正則値 y について、 y の逆像 f ^-1(y) は有限集合である。よって、正則値 y に対して整数

${\displaystyle d(y):=\sum _{x\in f^{-1}(y)}\operatorname {sign} df_{x}}$

を定義することができる。ただし、df_x は f の x における微分、 sign df_x は df_x （を行列としてみたとき）の行列式の符号^[1]である。

このように定義すると、 任意の正則値 y について d(y) は deg f と等しい。

性質

• 写像 f と g がホモトピックであれば、 deg f = deg g である。
• N = Sⁿ であれば、写像 f と g がホモトピックであることと deg f = deg g であることは同値である（ホップの定理）。

例

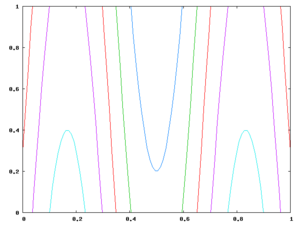
S¹ → S¹ の写像は S¹ × S¹、つまりトーラス上にグラフを描くことができる。下の図は、それぞれ写像度 -4, 0, 3の写像のグラフである。

脚注

1. f が x において向きを保つときに 1, 向きを逆転させるときに -1 の値をとる

参考文献

• 田村一郎 『トポロジー』 岩波全書
• John W. Milnor, Topology from the Differentiable Viewpoint, PRINCETON UNIVERSITY PRESS

関連項目

• 位相幾何学
• 多様体
• ホモトピー
• ホモロジー