スピンエコー法
磁気共鳴におけるスピンエコー法(スピンエコーほう、英: spin echo、SE)は、歳差スピン磁化の共鳴放射パルスによるリフォーカスである。現代の核磁気共鳴 (NMR) ならびに核磁気共鳴画像法 (MRI) は、この効果に依存するところが大きい。
励起パルスの後に観測されるNMRシグナルは、スピン-スピン緩和ならびに異なるスピンが異なる速度で歳差運動する原因となる全ての「不均一」効果(例えば化学シフトの分布あるいは磁場勾配)によって時間とともに減衰する。緩和の結果として不可逆的な磁化の損失(デコヒーレンス)が起こるが、不均一な離調は磁化ベクトルを反転させる180°パルスあるいは「反転」パルスを適用することにより逆転させることができる。
現在最も一般的に用いられるパルス系列であり、90°パルス-180°パルスの組み合わせを一定間隔 (1TE) で連続的に印加する。均一静磁場中の核スピンに対して、まず90°パルスを印加し、巨視的磁化ベクトルをx-y平面上に倒す。90°パルス印加直後から、核スピンが定常状態に戻る緩和の過程で、巨視的磁化ベクトルはT2*の時定数で消失する自由誘導減衰 (FID) 信号を放出するが、この途中で、90°パルス印加からτ(TE/2)時間後に180°パルスを印加すると、各核スピンの角速度がキャンセルされ、τ時間後に、T2の時定数で求められる信号強度に該当するエコー信号が観測される。これがスピンエコーである。Short-TR&TEでT1強調画像を、Long-TR&TEでT2強調画像を得ることができる。スピン-格子緩和(spin-lattice relaxation)ともいう。
エコー現象は、レーザー分光法[1]や中性子散乱などの磁気共鳴以外の分野での使用されるコヒーレント分光法の重要な要素である。エコーは最初1950年にアーウィン・ハーンによって核磁気共鳴において検出され[2]、スピンエコーは「ハーンエコー」と呼ばれることがある。核磁気共鳴や核磁気共鳴画像法の分野では、高周波照射が最も一般的に使用される。
原理
[編集]アーウィン・ハーンのスピンエコーのコンセプトは1950年の彼の論文で解説されており[2]、180°リフォーカシングパルスの利点を指摘したカー (Carr) とパーセルによって更に発展した[3]。
パルスシークエンスは以下の段階に分解することでより理解することができる。

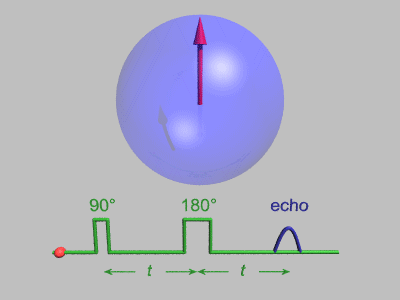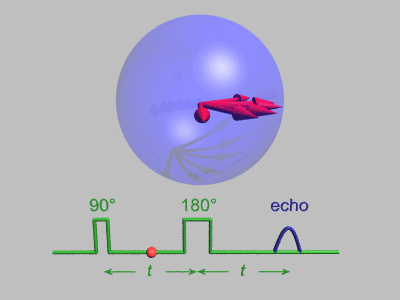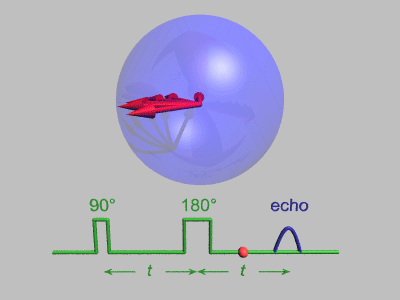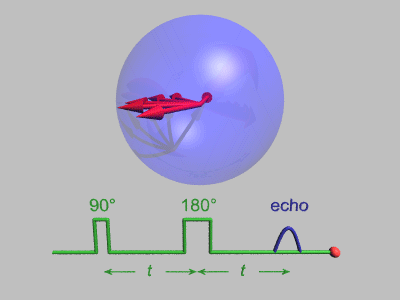
スピンエコーシークエンス A) - 垂直の赤矢印はプロトンといったスピンの一つの集団の平均磁気モーメントである。全ては垂直磁場中で垂直に位置し、長軸に沿ってスピンしている。しかしこのイラストは、スピンが平均すると静止している回転座標系である。B) 90°パルスを印加し、巨視的磁化ベクトルをx-y平面上に倒す。C) 局所的な磁場の不均一性(時間に対して不変なサンプルの異なる部分での磁場のばらつき)のため、減速するスピンと逆に加速し前方に出るスピンが生じる。これによってシグナルの減衰が起こる。D) 遅いスピンが主モーメントよりも前方に出て、速いスピンが逆に後方になるように180°パルスを印加する。E) 次第に速いモーメントは主モーメントに追い付き、遅いモーメントは主モーメントに戻っていく。F) 完全なリフォーカスが起こり、この時全ての効果が除去された正確なエコーを計測することができる。図では示されていないが、全く独立した赤矢印の垂直方向への回復は緩和を反映している。
このアニメーションではいくつかの単純化が行われている(デコヒーレンスが含まれていない)。
180度はラジアンであるため、180° パルスはしばしばと呼ばれる。
ハーンエコー減衰
[編集]ハーンエコー減衰実験は、下のアニメーションに見るような位相散逸時間を測定するために用いることができる。2つのパルスの幅を変化させ、エコーの大きさを記録することによって、パルスによってリフォーカスされないデコヒーレンスを明らかにすることができる。ある場合は、時間で表される指数関数的減衰が測定される。
刺激エコー
[編集]ハーンの1950年の論文[2]では、スピンエコーを精製するため、三連続90°パルスを印加するもう一つの手法が示されている。初めの90°パルスの後、磁化ベクトルは上の図に示しているように拡散し、x-y平面にパンケーキのような広がりを形成する。この拡散は時間続き、次に「パンケーキ」がx-z平面に移動するように二番目の90°パルスが印加される。さらに時間後、三番目のパルスが印加され、最後のパルスの時間後に刺激エコー (stimulated echo) が観測される。
光子エコー
[編集]ハーンエコーは、光周波数においても観測される[1]。この場合、共鳴光は不均一に拡がった吸収共鳴を持つ物体に対して照射される。磁場中の2つのスピン状態を用いる代わりに、光子エコー (photon echo) はゼロ磁場においても物質中に存在する2つのエネルギーレベルを使用する[4]。
脚注
[編集]- ^ a b Kurnit, N. A.; Abella, I. D.; Hartmann, S. R. (1964). “Observation of a photon echo”. Physical Review Letters 13: 567–568. Bibcode: 1964PhRvL..13..567K. doi:10.1103/PhysRevLett.13.567.
- ^ a b c Hahn, E.L. (1950). “Spin echoes”. Physical Review 80: 580–594. Bibcode: 1950PhRv...80..580H. doi:10.1103/PhysRev.80.580.
- ^ Carr, H. Y.; Purcell, E. M. (1954). “Effects of Diffusion on Free Precession in Nuclear Magnetic Resonance Experiments”. Physical Review 94: 630–638. Bibcode: 1954PhRv...94..630C. doi:10.1103/PhysRev.94.630.
- ^ The Babbitt Rf Photonics Group. “Basics of OCTs”. 2011年11月11日閲覧。
教科書
[編集]- Ray Freeman (1999). Spin Choreography: Basic Steps in High Resolution NMR. Oxford University Press. ISBN 978-0-19-850481-8
- Malcolm H. Levitt (2001). Spin Dynamics: Basics of Nuclear Magnetic Resonance. Wiley. ISBN 978-0471489221
- Arthur Schweiger, Gunnar Jeschke (2001). Principles of Pulse Electron Paramagnetic Resonance. Oxford University Press. ISBN 978-0198506348






