ノノミノ
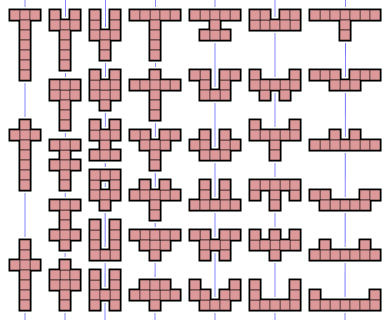
ノノミノ(英語:Nonomino)またはエネオミノ(英語:Enneomino)または9-オミノは、位数9のポリオミノである。同じ大きさの9個の正方形を辺に沿ってつなげた形を総称してノノミノという[1](pp74,116,156,157)。
ノノミノやエネオミノという名称は、9を意味する接頭語の"nona"や"ennéa"とポリオミノの"omino"を組み合わせた語である。
回転操作や鏡映操作で同一になるものを1つとして数えると、1285種のノノミノが存在する。鏡像を別物とすると、2500種の片面型ノノミノが存在する。(90度の倍数の)回転も別物とした有向ノノミノは9910種である[2]。
対称性
[編集]1285個あるノノミノは、対称性によって分類することができる[2]。
- 1196種のノノミノは対称性を持たない。
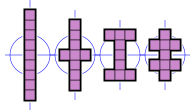
- 38種のノノミノは、辺に平行な対称軸を持つ1軸対称である。
- 26種のノノミノは、正方形の対角線に平行な対称軸を持つ1軸対称である。
- 19種のノノミノは、180度回転対称である。
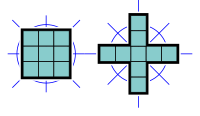
- 4種のノノミノは、2つの対称軸を持つ線対称形でありかつ180度回転対称である。
- 2種のノノミノは、4本の対称軸を持つ線対称形でありかつ90度回転対称である。
オクトミノと違い、「線対称でないが90度回転対称」や「対角線方向の対称軸を持つ2軸対称」のノノミノは存在しない。
第1群と第4群は自身と鏡像が違う形になる。よって、片面型ノノミノは 1285+1196+19=2500種類となる。鏡像と回転を別物としたとき、1群は鏡像と回転で8種類の変種がある。2,3,4群は4通り、5群は2通りの変種があるため、有向ノノミノは 1196×8+(38+26+19)×4+4×2+2=9910種類となる。
箱詰めと敷き詰め
[編集]
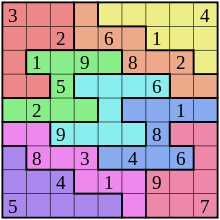
37種類のノノミノには穴がある[3][4]。このためすべてのノノミノを使用して長方形を作ることはできない。また、平面充填が不可能なものがある。1050種類のノノミノが平面充填可能である[5]が、そのうちの2種類はコンウェイの基準(英語)を満たさない。ノノミノは、この基準を満たさずに平面充填可能なポリオミノが存在する最小のものである[6]。
以下が穴のある37種類のノノミノである。1つ(最上段右から2番目)は2単位の穴がある。これは2単位の穴を持つ最小のポリオミノである。

脚注
[編集]- ^ Golomb, Solomon W. (1994). Polyominoes (2nd ed.). Princeton, New Jersey: Princeton University Press. ISBN 0-691-02444-8
- ^ a b Redelmeier, D. Hugh (1981). “Counting polyominoes: yet another attack”. Discrete Mathematics 36: 191–203. doi:10.1016/0012-365X(81)90237-5.
- ^ Weisstein, Eric W. "Polyomino". mathworld.wolfram.com (英語).
- ^ Sloane, N.J.A. (ed.). "Sequence A001419 (穴がある n-オミノの数)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. 2023年1月6日閲覧。
- ^ Rawsthorne, Daniel A. (1988). “Tiling complexity of small n-ominoes (n<10)”. Discrete Mathematics 70: 71–75. doi:10.1016/0012-365X(88)90081-7.
- ^ Rhoads, Glenn C. (2005). “Planar tilings by polyominoes, polyhexes, and polyiamonds”. Journal of Computational and Applied Mathematics 174 (2): 329–353. doi:10.1016/j.cam.2004.05.002.