プラクティカル数

12がプラクティカル数であることの図的説明

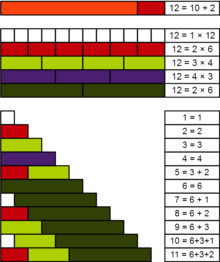
数論において、プラクティカル数 (practical number; 実際数^[1]) もしくはパナリズミック数 (pan­arithmic number^[2]; 汎数的数) とは約数の和でその数より小さな正の整数すべてが表せる自然数である。例えば、12は約数1,2,3,4,6を持ち、1から11までの整数は、1,2,3,4,6の和として表せるため、12はプラクティカル数である。（5 = 3 + 2, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1, 11 = 6 + 3 + 2）

プラクティカル数の数列はオンライン整数列大辞典の数列 A005153に記載されており、

1, 2, 4, 6, 8, 12, 16, 18, 20, 24, 28, 30, 32, 36, 40, 42, 48, 54, 56, 60, 64, 66, 72, 78, 80, 84, 88, 90, 96, 100, 104, 108, 112, 120, 126, 128, 132, 140, 144, 150....

と続く。

1202年、フィボナッチは算盤の書で、エジプト式分数として有理数を表す問題にプラクティカル数を用いた。フィボナッチはプラクティカル数を正確に定義したわけではないが、フィボナッチはプラクティカル数を分母とする分数のエジプト式分数表現の表を与えた^[3]。

プラクティカル数という名前はSrinivasan (1948)に由来する。スリニヴァサンは「金・重さ・長さの単位は4, 12, 16, 20, 28のような数で細分化されており、10の累乗での細分化に置き換えるべき不便さである。」と述べた。スリニヴァサンはそのような数の数論的な性質を再発見し、Stewart (1954)とSierpiński (1955)によってこのような数の分類が完了した。この特徴付けにより、素因数分解によって与えられた数がプラクティカル数であるかを判別できるようになった。偶数の完全数と2のべき乗は、すべてプラクティカル数である。

プラクティカル数は素数と様々な性質で関連付けられている^[4]。

プラクティカル数の特徴

プラクティカル数の最初の特徴付けは、Srinivasan (1948)によって行われたもので、プラクティカル数は不足が2以上である不足数にはなりえないというものである。不足数とは(自身を除く)約数の和がそれ自身より小さい数であり、ここでは約数の和がそれ自身より2以上小さい数のみを指す。もし n の(1と自身を含む)約数の順序集合を${\displaystyle {d_{1},d_{2},...,d_{j}}}$ 、 ${\displaystyle d_{1}=1}$ 、 ${\displaystyle d_{j}=n}$とすると、スリニヴァサンの特徴付けは以下の不等式に対応する

${\displaystyle 2n\leq 1+\sum _{i=1}^{j}d_{i}}$.

言い換えると、プラクティカル数のすべての約数を小さい順に並べた${\displaystyle {d_{1}<d_{2}<...<d_{j}}}$はcomplete sub-sequenceである。

この部分的特徴付けは、Stewart (1954) と Sierpiński (1955) により拡張され、素因数分解を用いてある数がプラクティカル数かどうかを判別できることが示された。 1より大きな正の整数を素因数分解し、${\displaystyle n=p_{1}^{\alpha _{1}}...p_{k}^{\alpha _{k}}}$と表す。ここで、素数は小さい順に${\displaystyle p_{1}<p_{2}<\dots <p_{k}}$と並んでいるものとする。このとき、${\displaystyle n}$がプラクティカル数であるのは、各素因数${\displaystyle p_{i}}$が十分小さく、${\displaystyle p_{i}-1}$がより小さな約数の和で表せるとき、かつそのときに限る。 これが真であるためには、（1以外の）プラクティカル数の最小の素因数${\displaystyle p_{1}}$は2であり、 i ( 2 〜 k） に対して、次の素数${\displaystyle p_{i}}$は以下の不等式に従わなければならない。

${\displaystyle p_{i}\leq 1+\sigma (p_{1}^{\alpha _{1}}p_{2}^{\alpha _{2}}\dots p_{i-1}^{\alpha _{i-1}})=1+\prod _{j=1}^{i-1}{\frac {p_{j}^{\alpha _{j}+1}-1}{p_{j}-1}},}$

ここで、${\displaystyle \sigma (x)}$はxの約数の和である。 例えば、2 × 3² × 29 × 823 = 429606について考えると、

3 ≤ σ(2) + 1 = 4

29 ≤ σ(2 × 3²) + 1 = 40

823 ≤ σ(2 × 3² × 29) + 1 = 1171

と不等式を満たすので、429606はプラクティカル数である。

この条件は自然数がプラクティカル数であるための必要十分条件である。${\displaystyle p_{i}-1}$をnの約数の和で表すためにはこの条件が必要であり、数学的帰納法によって十分条件であることもわかる。 より強い条件として、nの 素因数分解が上記の条件を満たすならば、任意の${\displaystyle m\leq \sigma (n)}$は以下のように n の約数の和で表現できる^[5]。

• ${\displaystyle q=\min\{\lfloor m/p_{k}^{\alpha _{k}}\rfloor ,\sigma (n/p_{k}^{\alpha _{k}})\}}$となる qと、${\displaystyle r=m-qp_{k}^{\sigma _{k}}}$となる rを用意する
• ${\displaystyle q\leq \sigma (n/p_{k}^{\alpha _{k}})}$ であり ${\displaystyle n/p_{k}^{\alpha _{k}}}$ がプラクティカル数であることより、${\displaystyle n/p_{k}^{\alpha _{k}}}$の約数の和で q を表せる。
• ${\displaystyle r\leq \sigma (n)-p_{k}^{\alpha _{k}}\sigma (n/p_{k}^{\alpha _{k}})=\sigma (n/p_{k})}$であり、${\displaystyle n/p_{k}}$はプラクティカル数であることから、${\displaystyle n/p_{k}}$の約数の和で r を表せる。
• r を表す約数と、 q を表す約数のそれぞれを${\displaystyle p_{k}^{\alpha _{k}}}$倍すると、 m は n の約数で表せる。

性質

• 奇数のプラクティカル数は1のみである。2以上の奇数は2を約数の和として表せない。さらに、Srinivasan (1948)は1と2を除くすべてのプラクティカル数は4または6の倍数であることを示した。
• 2つのプラクティカル数の積はプラクティカル数である^[6]。さらに、2つのプラクティカル数の 最小公倍数もプラクティカル数である。つまり、プラクティカル数すべての集合は積について閉じている。
• スチュワートとシェルピンスキーによる上記の性質から、もし n がプラクティカル数であり、 d がその約数であれば、 ndもプラクティカル数である。
• すべてのプラクティカル数からなる集合において、プラクティカル数のプリミティブ集合が存在する。プリミティブプラクティカル数は、平方因子を持たないプラクティカル数か素因数分解の素数の次数が2以上であるような素因数で割った場合にプラクティカル数ではなくなるプラクティカル数である。このようなプリミティブプラクティカル数の数列は オンライン整数列大辞典の数列 A267124 で

1, 2, 6, 20, 28, 30, 42, 66, 78, 88, 104, 140, 204, 210, 220, 228, 260, 272, 276, 304, 306, 308, 330, 340, 342, 348, 364, 368, 380, 390, 414, 460 ...

と続く。

ほかの数との関係

有名な整数からなる集合は、プラクティカル数のみから構成できることがある。

• 上記の性質から、 プラクティカル数 n とその約数 dに対して、ndもプラクティカルであるため、2のべき乗の6倍と3のべき乗の6倍はプラクティカル数である。
• すべての2のべき乗はプラクティカル数である。^[7]。 2のべき乗は素因数分解により上記の必要条件を満たし、p₁=2も満たす。
• すべての偶数の完全数は、プラクティカル数である^[7]。偶数の完全数は 2^n-1(2ⁿ-1)の形である結果から導ける。素因数分解の奇数部分は偶数部分の約数の和である。従って、偶数の完全数はプラクティカル数である。
• すべての素数階乗 (最小のi個の素数の積）はプラクティカル数である^[7]。1つめの素数階乗の2と2つめの素数階乗の6はプラクティカル数である。それ以降の素数階乗は素数 p_i と素数階乗の積であり、つまり2と次の最小の素数でp_i-1で割り切れる。ベルトランの仮説により、p_i<2p_i-1が成り立つので、次の素因数は前の素数階乗の約数よりも小さい。同様に、すべての素数階乗はプラクティカル数である性質を満たし、平方因子も含まない。
• 素数階乗を一般化し、最小の k 個の素数の累乗の積もプラクティカル数である。これはシュリニヴァーサ・ラマヌジャンの高度合成数（自然数のうち、それ未満のどの自然数よりも約数が多いもの）や階乗も含む^[7]。

プラクティカル数とエジプト式分数

n がプラクティカル数であれば、任意の有理数 m/n (m < n) は nの異なる約数を d_i としたときに、 ∑d_i/n で表せる。それぞれの項は単位分数に約分できるため、 m/n はエジプト式分数で表せる。例えば、

${\displaystyle {\frac {13}{20}}={\frac {10}{20}}+{\frac {2}{20}}+{\frac {1}{20}}={\frac {1}{2}}+{\frac {1}{10}}+{\frac {1}{20}}.}$

1202年、フィボナッチは『算盤の書』^[3]において、有理数のエジプト式分数での表現を見つける手法を列挙した。このうち、最初の処理は、その数が単位分数であるかの判別であるが、2つめの処理は、上述のように分母の約数の合計として分子の表現を探索することに対応する。この手法はプラクティカル数である分母に対してのみ成功することが保証されている。フィボナッチは分母として、6, 8, 12, 20, 24, 60, 100を用い、これらについての表を与えた。.

Vose (1985)は任意の数 x/y に対してたかだか${\displaystyle \scriptstyle O({\sqrt {\log y}})}$ 項でのエジプト式分数の表現が存在することを示した。この証明にはプラクティカル数の列n_iを見つける処理が含まれており、n_i以下のそれぞれの数に対してたかだか${\displaystyle \scriptstyle O({\sqrt {\log n_{i-1}}})}$個の異なるn_iの約数が存在することを用いる。ここで、 i は n_{i - 1}<y≤n_iであり、 xn_i は yで割ったときに商 q とあまり r をもつ。これにより${\displaystyle \scriptstyle {\frac {x}{y}}={\frac {q}{n_{i}}}+{\frac {r}{yn_{i}}}}$となる。それぞれの分子を展開することで、所望のエジプト式分数の表現が得られる。Tenenbaum & Yokota (1990)は異なるプラクティカル数の数列を含んだ似た手法を用い、任意の有理数 x/y がエジプト式分数の表現を持ち、その最大の分母が ${\displaystyle \scriptstyle O({\frac {y\log ^{2}y}{\log \log y}})}$であることを示した。

孫智偉が2015年9月に出した予想によれば、すべての正の有理数は、分母がすべてプラクティカル数であるエジプト式分数の表現を持つ。^[8]そしてその証明はデビッド・エップシュタインのブログにある^[9]。

素数とのアナロジー

プラクティカル数に興味が集まっている理由の一つに、素数との類似性がある。実際、ゴールドバッハの予想や双子素数の予想はプラクティカル数に対しては知られている（すべての偶数は2つのプラクティカル数の和で表せる。x-2, x, x+2がすべてプラクティカル数である三つ組みが存在する）^[10]。ギウゼッペ・メルフィはプラクティカル数であるフィボナッチ数が無限に存在することを示したオンライン整数列大辞典の数列 A124105。フィボナッチ素数が無限に存在するかはまだ未解決問題である。Hausman & Shapiro (1984)は正の実数xに対して、[x²,(x+1)²]の範囲に少なくとも一つのプラクティカル数が存在することを示した。これは素数に対するルジャンドル予想（未解決）である。

p(x) を、x以下のプラクティカル数の数とする。 Margenstern (1991)は、 p(x) は cx/logx に漸近すると予想した（ c は定数）。この形は素数定理の素数の個数と似ており、Erdős & Loxton (1979) がプラクティカル数の整数内での濃度が0であることのより強い主張である。 Saias (1997)はその定数について、 c₁ と c₂を適切に設定することで

${\displaystyle c_{1}{\frac {x}{\log x}}<p(x)<c_{2}{\frac {x}{\log x}}}$

となることを証明した。

Weingartner (2015) はモルゲンシュタインの予想を以下のように証明した。

${\displaystyle p(x)={\frac {cx}{\log x}}\left(1+O\!\left({\frac {\log \log x}{\log x}}\right)\right)}$

この定数 ${\displaystyle c}$は^[11]によって与えられる。

${\displaystyle c={\frac {1}{1-e^{-\gamma }}}\sum _{n\ {\text{practical}}}{\frac {1}{n}}{\Biggl (}\sum _{p\leq \sigma (n)+1}{\frac {\log p}{p-1}}-\log n{\Biggr )}\prod _{p\leq \sigma (n)+1}\left(1-{\frac {1}{p}}\right),}$

ここで、 ${\displaystyle \gamma }$ はオイラー・マスケローニ定数であり、 ${\displaystyle p}$ は素数である。この結果、${\displaystyle 1.311<c<1.693}$^[11]であり、プラクティカル数は素数に比べて31.1% から 69.3% 多いことがわかる。

脚注

1. James J. Tattersall『初等整数論9章』（第2）森北出版、2008年9月。ISBN 978-4-627-08162-8。https://www.morikita.co.jp/books/book/470。  (見本 (PDF) )
2. Margenstern (1991) cites Robinson (1979) and Heyworth (1980) for the name "pan­arithmic numbers".
3. ^ Sigler (2002).
4. Hausman & Shapiro (1984); Margenstern (1991); Melfi (1996); Saias (1997)
5. Stewart (1954); Sierpiński (1955)
6. Margenstern (1991).
7. ^ Srinivasan (1948)
8. A Conjecture on Unit Fractions Involving Primes
9. 0xDE: Egyptian fractions with practical denominators
10. Melfi (1996)
11. ^ Weingartner (2019)

参考文献

• Erdős, Paul; Loxton, J. H. (1979), “Some problems in partitio numerorum”, Journal of the Australian Mathematical Society (Series A) 27 (03): 319–331, doi:10.1017/S144678870001243X .
• Heyworth, M. R. (1980), “More on panarithmic numbers”, New Zealand Math. Mag. 17 (1): 24–28 . As cited by Margenstern (1991).
• Hausman, Miriam; Shapiro, Harold N. (1984), “On practical numbers”, Communications on Pure and Applied Mathematics 37 (5): 705–713, doi:10.1002/cpa.3160370507, MR0752596 .
• Margenstern, Maurice (1984), “Résultats et conjectures sur les nombres pratiques”, Comptes Rendus de l'Académie des Sciences, Série I 299 (18): 895–898 . As cited by Margenstern (1991).
• Margenstern, Maurice (1991), “Les nombres pratiques: théorie, observations et conjectures”, Journal of Number Theory 37 (1): 1–36, doi:10.1016/S0022-314X(05)80022-8, MR1089787 .
• Melfi, Giuseppe (1996), “On two conjectures about practical numbers”, Journal of Number Theory 56 (1): 205–210, doi:10.1006/jnth.1996.0012, MR1370203 .
• Mitrinović, Dragoslav S.; Sándor, József; Crstici, Borislav (1996), “III.50 Practical numbers”, Handbook of number theory, Volume 1, Mathematics and its Applications, 351, Kluwer Academic Publishers, pp. 118–119, ISBN 978-0-7923-3823-9 .
• Robinson, D. F. (1979), “Egyptian fractions via Greek number theory”, New Zealand Math. Mag. 16 (2): 47–52 . As cited by Margenstern (1991) and Mitrinović, Sándor & Crstici (1996).
• Saias, Eric (1997), “Entiers à diviseurs denses, I”, Journal of Number Theory 62 (1): 163–191, doi:10.1006/jnth.1997.2057, MR1430008 .
• Sigler, Laurence E. (trans.) (2002), Fibonacci's Liber Abaci, Springer-Verlag, pp. 119–121, ISBN 0-387-95419-8 .
• Sierpiński, Wacław (1955), “Sur une propriété des nombres naturels”, Annali di Matematica Pura ed Applicata 39 (1): 69–74, doi:10.1007/BF02410762 .
• Srinivasan, A. K. (1948), “Practical numbers”, Current Science 17: 179–180, MR0027799, http://www.currentscience.ac.in/Downloads/article_id_017_06_0179_0180_0.pdf .
• Stewart, B. M. (1954), “Sums of distinct divisors”, American Journal of Mathematics (The Johns Hopkins University Press) 76 (4): 779–785, doi:10.2307/2372651, JSTOR 2372651, MR0064800, https://jstor.org/stable/2372651 .
• Tenenbaum, G.; Yokota, H. (1990), “Length and denominators of Egyptian fractions”, Journal of Number Theory 35 (2): 150–156, doi:10.1016/0022-314X(90)90109-5, MR1057319 .
• Vose, M. (1985), “Egyptian fractions”, Bulletin of the London Mathematical Society 17 (1): 21, doi:10.1112/blms/17.1.21, MR0766441 .
• Weingartner, A. (2015), “Practical numbers and the distribution of divisors”, The Quarterly Journal of Mathematics 66 (2): 743–758, arXiv:1405.2585, doi:10.1093/qmath/hav006 .
• Weingartner, A. (2019), “On the constant factor in several related asymptotic estimates”, Mathematics of Computation 88: 1883-1902, arXiv:1705.06349, doi:10.1090/mcom/3402 .

外部リンク

• Tables of practical numbers compiled by Giuseppe Melfi.
• Practical Number - PlanetMath.（英語）
• Weisstein, Eric W. "Practical Number". mathworld.wolfram.com (英語).