ルンゲ現象

赤はコーシー・ローレンツ関数。青は5次の補間多項式。緑は9次の補間多項式（補間点は等間隔）。 補間点では関数と補間多項式は誤差が（定義上）ゼロである。補間点と補間点の間（特に 1 や −1 に近い部分）では、補間多項式を高次にした方が誤差が大きくなっている。

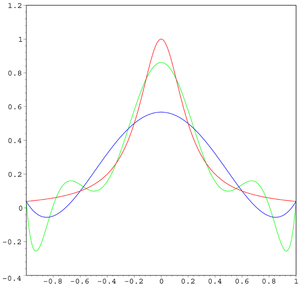
ルンゲ現象（ルンゲげんしょう、英語: Runge's phenomenon）は、（与えられた分点集合上で）関数を高次の多項式を用いて多項式補間を行なう際に発生しがちな問題である。カール・ルンゲが、ある関数を多項式補間で近似したときの誤差を調べていて発見した^[1]。 補間点の集合を適切に選ぶことにより困難を回避できるが、良く用いられる等間隔の分点を選ぶと問題が発生し易い。 計算に用いる数値の精度に制限があるという理由でこの現象が生じるのではない。

問題

次の関数（コーシー-ローレンツ関数）を考える。

${\displaystyle f(x)={\frac {1}{1+25x^{2}}}}$

次のような −1 から 1 までの等間隔の点 x_i における値から、この関数を内挿する。

${\displaystyle x_{i}=-1+{\frac {2(i-1)}{n}},\quad i\in \left\{1,2,\dots ,n+1\right\}}$

このときルンゲは、次数 ≤ n の多項式 P_n(x) を用いると、区間の端の方（−1 および 1）に行くに従って補間結果が振動することを発見した。このことは、多項式の次数を大きくしていくと補間誤差の大きさの上限が無限大に漸近することで証明できる。

${\displaystyle \lim _{n\rightarrow \infty }\left(\max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|\right)=\infty }$

しかし、ワイエルシュトラスの近似定理によれば、誤差が零に近づくような近似多項式の列が存在するはずである。このことは、等間隔の分点分布を用いて高次多項式により補間を行なうと、問題が発生する場合があることを示している。

原因

関数とN次補間多項式の誤差は、関数のN次導関数に制限される。

上記示した関数の2次までの導関数は次のようになる。

${\displaystyle {\begin{aligned}f'(x)=-{\frac {50x}{\left(1+25x^{2}\right)^{2}}}&\Rightarrow \left|f'(1)\right|={\frac {50}{26^{2}}}\approx 0.0740\\f''(x)={\frac {5000x^{2}(1+25x^{2})-50(1+25x^{2})^{2}}{\left(1+25x^{2}\right)^{4}}}&\Rightarrow \left|f''(1)\right|={\frac {96200}{26^{4}}}\approx 0.2105\end{aligned}}}$

見てわかる通り、高次の導関数の方が大きくなっている。従って、（補間点間の）誤差の上限も補間多項式の次数が高くなるほど大きくなる。

緩和方法

補間多項式の振動を抑えるには、等間隔のノード（補間点）ではなくてチェビシェフノード（英語版）を使うのが良い。チェビシェフノードは補間の次数を上げるにつれて、区間の両端でしだいに密になっていく性質がある。チェビシェフノードを採用する場合には、多項式の次数を上げていくと誤差の大きさが減少することが保証される。等間隔ノードを採用して近似区間全体に渡って単一の高次多項式で補間を行なうことは、一般にはルンゲ現象が発生するので不適切である。あるいはスプライン曲線による近似を用いる方法もある。スプライン曲線は近似を行なう区間全体にわたる単一の多項式を近似関数として採用するのではなくて、近似を行う区間を小区間に分割して、各小区間内では比較的低次の多項式を採用する。そうして区分的な多項式で表される近似関数が隣り合う小区間の境界点である程度の滑らかさを持つように各小区間内の多項式を決めるという方法である。スプライン補間法の場合には、各小区間内の多項式の次数を上げずに、各小区間の幅（等間隔でも良い）を一様に減らすことで補間誤差の大きさを減らすことができる。

脚注

[脚注の使い方]

1. Runge, Carl (1901年), “Über empirische Funktionen und die Interpolation zwischen äquidistanten Ordinaten”, Zeitschrift für Mathematik und Physik 46: 224–243 

関連項目

• ギブズ現象