像面湾曲
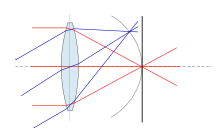
像面湾曲(ぞうめんわんきょく field curvature) とは、光学系の前側と後側で、光学系に平行な焦点面が平面から平面に対応しないという収差である。
球面収差、非点収差、コマ収差、歪曲収差と並んでザイデル収差の一つである[1][2]。
ほとんど全ての接眼レンズの像面は、対象側に凸に湾曲している[2]。
概要
[編集]単純な球面凸レンズ1枚の場合、前後の焦点面が、周辺部がレンズ側に寄るような形でそれぞれ湾曲している。単純な光学系ほど、それに似たような傾向になりやすい。無限遠の撮影や書類の複写などの場合は重要だが、近距離の静物をいわゆる日の丸構図で撮るような場合などはあまり気にならないかもしれない。テストチャートの撮影、あるいは、カメラのフィルム面にスライドフィルムを通して逆に投影するチャート投影テスト等では影響が大きい。
VFCロッコール(VFC: Variable Field Curvature)のように、撮影者の意図で調整できるようにした写真レンズもある。
像面湾曲は非点収差と密接な関係にある。像面湾曲による像面が、同心円方向の像と、直径方向の像で異なった面になっていると、それが非点収差になる。写真レンズの場合には、像面湾曲の補正は比較的甘いが、同心円方向と直径方向の像面一致に注力し非点収差を抑えてある、という個性の場合がある。前述のように、平面の撮影となるチャートでのテストではデフォーカス像となるため、周辺部で解像が悪くなるが、一般の撮影では非点収差が抑えられているため綺麗なボケ像の写真が得られる。
解決手段
[編集]ジョセフ・マキシミリアン・ペッツヴァールが発見したペッツヴァール条件を満たした場合、像面は平面になる[2]。
シュミット式望遠鏡や、カメラではミノックスやレンズ付きフィルムが著名であるが(実施例は他にも多い)、レンズ非交換式カメラ等でそのレンズの特性がわかっている場合、フィルムを長辺側で湾曲させて像面に少しでも沿わせるという手法もある[3]。
反射光学系
[編集]グレゴリー式望遠鏡では主鏡も副鏡も凹面であるため像面は前方に向かって凸に強く湾曲するが、接眼レンズの像面湾曲によりある程度打ち消される[2]。カセグレン式望遠鏡では主鏡が凹面、副鏡が凸面であるため像面は比較的平坦である[2]。シュミットカセグレン式望遠鏡では特別な条件を満足する場合正確な平面像面が得られる[2]。
出典・注
[編集]参考文献
[編集]- 吉田正太郎『天文アマチュアのための望遠鏡光学・屈折編』誠文堂新光社、1989年。ISBN 4-416-28908-1。
- 吉田正太郎『天文アマチュアのための望遠鏡光学・反射編』誠文堂新光社、1988年。ISBN 4-416-28813-1。