分子対称性

化学における分子の対称性（ぶんしのたいしょうせい、英: molecular symmetry）は、分子に存在する対称性およびその対称性に応じた分子の分類を述べる。分子対称性は化学における基本概念であり、双極子モーメントや許容分光遷移（ラポルテの規則といった選択則に基づく）といった分子の化学的性質の多くを予測あるいは説明することができる。多くの大学レベルの物理化学や量子化学、無機化学の教科書は、対称性のために一章を割いている^[1]^[2]^[3]^[4]^[5]。

分子の対称性の研究には様々な枠組みが存在するが、群論が主要な枠組みである。この枠組みは、ヒュッケル法、配位子場理論、ウッドワード・ホフマン則といった応用に伴って分子軌道の対称性の研究にも有用である。大規模な系では、固体材料の結晶学的対称性を説明するために結晶系が枠組みとして使用されている。

分子対称性を実質的に評価するためには、X線結晶構造解析や様々な分光学的手法（例えば金属カルボニルの赤外分光法）など多くの技術が存在する。

概念

分子の対称性の研究は、数学で使われる群論の適応である。

キラリティーと対称性との間の関係の例
回転軸 (C_n)	回映要素 (S_n)
	キラル S_nなし	アキラル鏡面 S₁ = σ	アキラル反転中心 S₂ = i
C₁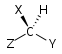
C₂

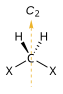要素

分子の対称性は5種類の対称要素（英語版）によって表すことができる。

対称軸: ${\tfrac {360^{\circ }}{n}}$ 周りを回転させると元の分子と区別が付かない分子を生じる軸。n-回回転軸とも呼ばれ、C_nと略される。例えば、水はC₂、アンモニアはC₃である。分子は一つ以上の対称軸を持つことができる、最も高いnを持つ軸は主軸と呼ばれ、慣習的に直交座標系におけるz軸に割り当てられる。
対称面: 鏡映で与えられる鏡像が元の分子と同一となる面。鏡面とも呼ばれ、σと略される。水には対称面が2つある。1つは分子平面それ自身であり、もう一つは分子平面に対して垂直な面である。主軸に対して平行な（主軸を含む）対称面はvertical（σ_v）、主軸に対して垂直な対称面はhorizonal（σ_h）と呼ばれる。対称面にはもう一種類存在する。もし、vertical対称面が主軸に対して垂直な2本の2回回転軸の間でさらに角を二等分する場合、この面はdihedral（σ_d）と呼ばれる。対称面は直交座標系における方向（例えば (xz) あるいは (yz) など）でも分類することができる。
対称中心あるいは反転中心: iと略される。ある中心から正反対の等しい距離に同一の原子が存在する時、分子は対称中心を持つ。中心は原子の場合もあるしそうでない場合もある。例えば四フッ化キセノンはXe原子が反転中心であり、ベンゼン (C₆H₆) は環の中心が反転中心である。
回映軸: ${\tfrac {360^{\circ }}{n}}$ 周りを回転させた後に軸に対して垂直な面での鏡映によって分子が変化しない軸。n回回映軸とも呼ばれ、S_nと略される。例えば、正四面体型の四フッ化ケイ素は3つのS₄軸を持ち、エタンのねじれ型配座は1つのS₆軸を持つ。
恒等: 単一性を意味するドイツ語EinheitからEと略される。この対称要素は単に無変化からなり、全ての分子がこの要素を持つ。この要素は物理的に取るに足りないものに見えるが、その考慮は群論機構が適切に働くために必須である。

操作

平面四角形構造を持つXeF₄は1つのC₄軸とC₄に直交した4つのC₂軸を持つ。これらの5つの軸とC₄に垂直な鏡面が分子のD_4h対称群を定義する。

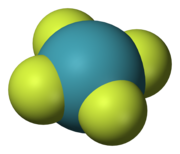
5つの対称要素は5種類の対称操作と関連している。これらはしばしば（常にではないが）各要素とキャレットによって区別される。ゆえに、Ĉ_nは軸を中心とした分子の回転であり、Êは恒等操作である。対称要素は、2つ以上の関連した対称操作を持つことができる。例えば四角形分子である四フッ化キセノン（XeF₄）は、逆向きの2つのĈ₄回転（90°）および1つのĈ₂回転（180°）と関連している。C₁（1回回転対称）はE（恒等）と、S₁（1回回映）はσ（鏡映）と、S₂（2回回映）はi（反転中心）と等価であるため、全ての対称操作は回転操作あるいは回映操作として分類することができる。

点群

点群は数学的な「群」を形成する一連の対称操作である。点群では少なくとも一つの「点」が群の全ての操作の下で固定されている。結晶点群は三次元における並進対称（英語版）と互換性がある点群である。合わせて32の結晶点群があり、そのうち30は化学に関連している。これらの分類はシェーンフリース記号に基づいている。

群論

以下の場合、一連の対称操作は操作の適用である作用素を持つ群を形成する。

2つの操作の連続した適用（合成、composition）の結果もまた同じ群に属する（閉包性）。
操作の適用が結合的である: A(BC) = (AB)C。
群が、群の全ての操作AについてAE = EA = Aとなる恒等操作を含んでいる。
群における全ての操作Aについて、群内に逆元A⁻¹が存在する: AA⁻¹ = A⁻¹A = E。

群の位数は、群の対称操作の数である。

例えば、水分子の点群はC_2vであり、対称操作のE、C₂、σ_v、σ_v'からなる。ゆえに位数は4である。それぞれの操作は自身の逆元である。閉包性の例としては、C₂回転とそれに続くσ_v鏡映はσ_v'のように見える：σ_v*C₂ = σ_v'（操作Aとそれに続くBによってCが作られることをBA = Cと書く）。

アンモニア分子はピラミッド型であり、3回回転軸および互いに120°の角度にある3つの鏡面を含んでいる。それぞれの鏡面はN-H結合を含んでおり、この結合と反対側のH-N-H結合角度を二等分する。ゆえに、アンモニア分子は位数6のC_3v点群に属する: 単位元E、2つの回転操作C₃およびC₃²、3つの鏡映操作σ_v、σ_v'、σ_v"。

一般的な点群

以下の表は代表的な分子の点群のリストを含んでいる。構造の説明は原子価殻電子対反発則（VSEPR則）に基づいた分子の一般的な形状である。

点群	対称操作	典型的な構造	例1	例2	例3
C₁	E	非対称、キラル	ブロモクロロフルオロメタン	リゼルグ酸
C_s	E σ_h	鏡面、その他の対称性はない	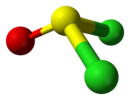塩化チオニル	次亜塩素酸	クロロヨードメタン
C_i	E i	反転中心	anti（英語版）-1,2-dichloro-1,2-dibromoethane
C_∞v	E 2C_∞ σ_v	直線状	フッ化水素	一酸化二炭素
D_∞h	E 2C_∞ ∞σ_i i 2S_∞ ∞C₂	反転中心を持つ直線状	酸素	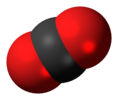二酸化炭素
C₂	E C₂	「開いた本の形状」、キラル	過酸化水素
C₃	E C₃	プロペラ、キラル	トリフェニルホスフィン
C_2h	E C₂ i σ_h	反転中心を持つ平面状	trans-1,2-ジクロロエチレン
C_3h	E C₃ C₃² σ_h S₃ S₃⁵	プロペラ	ホウ酸
C_2v	E C₂ σ_v(xz) σ_v'(yz)	屈曲型 (H₂O) あるいはシーソー型 (SF₄)	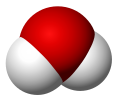水	四フッ化硫黄	フッ化スルフリル
C_3v	E 2C₃ 3σ_v	三角錐	アンモニア	塩化ホスホリル
C_4v	E 2C₄ C₂ 2σ_v 2σ_d	四角錐	四フッ化酸化キセノン
C_5v	E 2C₅ 2C₅² 5σ_v	「スツール」型錯体	Ni(C₅H₅)(NO)	コランニュレン
D₂	E C₂(x) C₂(y) C₂(z)	ねじれ、キラル	シクロヘキサンのねじれ舟形配座	ビフェニル
D₃	E C₃(z) 3C₂	三重らせん、キラル	トリス(エチレンジアミン)コバルト(III)カチオン	アセチルアセトンマンガン (III)
D_2h	E C₂(z) C₂(y) C₂(x) i σ(xy) σ(xz) σ(yz)	反転中心を持つ平面状	エチレン	四酸化二窒素	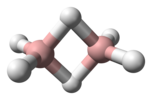ジボラン
D_3h	E 2C₃ 3C₂ σ_h 2S₃ 3σ_v	平面三角形あるいは三角両錐	三フッ化ホウ素	五塩化リン
D_4h	E 2C₄ C₂ 2C₂' 2C₂ i 2S₄ σ_h 2σ_v 2σ_d	平面四角形	四フッ化キセノン	オクタクロロ二モリブデン(II)酸アニオン
D_5h	E 2C₅ 2C₅² 5C₂ σ_h 2S₅ 2S₅³ 5σ_v	五角形	ルテノセン	C₇₀
D_6h	E 2C₆ 2C₃ C₂ 3C₂' 3C₂‘’ i 2S₃ 2S₆ σ_h 3σ_d 3σ_v	六角形	ベンゼン	ビス(ベンゼン)クロム
D_7h	E C₇ S₇ 7C₂ σ_h 7σ_v	七角形	トロピリウム (C₇H₇⁺) カチオン
D_8h	E C₈ C₄ C₂ S₈ i 8C₂ σ_h 4σ_v 4σ_d	八角形	シクロオクタテトラエニド (C₈H₈²⁻) アニオン	ウラノセン
D_2d	E 2S₄ C₂ 2C₂' 2σ_d	90°ねじれ	アレン	四硫化四窒素
D_3d	E C₃ 3C₂ i 2S₆ 3σ_d	60° ねじれ	エタン（ねじれ形回転異性体）	シクロヘキサンのいす型配座
D_4d	E 2S₈ 2C₄ 2S₈³ C₂ 4C₂' 4σ_d	45°ねじれ	デカカルボニル二マンガン（ねじれ形回転異性体）
D_5d	E 2C₅ 2C₅² 5C₂ i 3S₁₀³ 2S₁₀ 5σ_d	36°ねじれ	フェロセン（ねじれ形回転異性体）
S₄	E 2S₄ C₂		テトラフェニルホウ酸（英語版）アニオン
T_d	E 8C₃ 3C₂ 6S₄ 6σ_d	正四面体	メタン	五酸化二リン	アダマンタン
O_h	E 8C₃ 6C₂ 6C₄ 3C₂ i 6S₄ 8S₆ 3σ_h 6σ_d	正八面体あるいは立方体	キュバン	六フッ化硫黄
I_h	E 12C₅ 12C₅² 20C₃ 15C₂ i 12S₁₀ 12S₁₀³ 20S₆ 15σ	正二十面体	バックミンスターフラーレン	B₁₂H₁₂²⁻（英語版）	ドデカヘドラン

表現

対称操作は様々な方法で表現できる。便利な表現は行列によるものである。直交座標系における点を表現するいずれのベクトルにおいても、左からかけると対称操作によって変換された点の新しい位置を与える。操作の構成は行列の乗算と対応する。例えば、C_2vでは以下のようになる。

\underbrace {\begin{bmatrix}-1&0&0\\0&-1&0\\0&0&1\\\end{bmatrix}} _{C_{2}}\times \underbrace {\begin{bmatrix}1&0&0\\0&-1&0\\0&0&1\\\end{bmatrix}} _{\sigma _{v}}=\underbrace {\begin{bmatrix}-1&0&0\\0&1&0\\0&0&1\\\end{bmatrix}} _{\sigma '_{v}}

無数のこういった表現が存在するが、群の既約表現が一般的に使用され、その他全ての群の表現は既約表現の線形結合で表わすことができる。

指標表

それぞれの点群について、指標表はその対称操作および既約表現の情報を要約する。既約表現の個数と対称操作の共役類の個数は常に等しいので、表は正方形である。

表自身は、特定の対称操作を適用した時どのように特定の既約表現が変換されるかを表現した指標で構成されている。分子自身に作用する分子の点群におけるどの対称操作も分子を変化させない。しかし、ベクトルあるいは軌道といった一般実体にはこれはあてはまらない。ベクトルは符号あるいは方向性が変化し、軌道は種類が変化する。単純な点群では、値は1あるいは−1である。1は（ベクトルあるいは軌道の）符号あるいは位相が対称操作によって変化しないことを意味し（対称）、−1は符号が変化することを示す（非対称）。

表現は一連の慣習によって名前が付けられる。

A: 主軸の周りの回転が対称
B: 主軸の周りの回転が非対称
EおよびTはそれぞれ二重および三重に縮退した表現である。
点群が反転中心を持つ時、添字gは符号が反転に関して変化しないこと、添字uは符号が変化することを示す。
C_∞vおよびD_∞hについては、記号は角運動量の記述から借用されている（Σ、Π、Δ）。

表にはまた、デカルト座標系の基底ベクトル、それらやそれらの二次関数に関する回転が、群の対称操作によってどのように変換されるかという情報も記録されている。これらの表示は慣例的に表の右側に記載される。化学的に重要な軌道（特にpおよびd軌道）はこれらの実体と同じ対称性を有するため、この情報は有用である。

C_2v対称点群の指標表は以下の通りである。

C_2v	E	C₂	σ_v(xz)	σ_v'(yz)
A₁	1	1	1	1	z	x², y², z²
A₂	1	1	−1	−1	R_z	xy
B₁	1	−1	1	−1	x, R_y	xz
B₂	1	−1	−1	1	y, R_x	yz

C_2v対称性を有する水 (H₂O) の例を考える。酸素の2p_x軌道は分子の平面に対して垂直に向いており、C₂およびσ_v'(yz) 操作で符号が変化するが、その他2つの操作では変化しない。ゆえに、この軌道の指標集合は {1, −1, 1, −1} であり、B₁既約表現に対応する。同様に、2p_z軌道はA₁既約表現の対称性を、 2p_y軌道はB₂、3d_xy軌道はA₂を有する。

歴史的背景

ハンス・ベーテは1929年の配位子場理論の研究において点群操作の指標を使用し、ユージン・ウィグナーは原子分光学の選択則を説明するために群理論を使用した^[6]。初の指標表はティサ・ラースローによって振動スペクトルと結び付けて編纂された（1933年）。ロバート・マリケンは英語で初めて指標表を発表し（1933年）、E・ブライト・ウィルソンは固有振動の対称性を予測するために1934年にそれらを使用した^[7]。32種類の結晶点群一式はRosenthalとMurphyによって1936年に発表された^[8]。

非剛体分子

上で解説した対称群は、単一の平行構造に関して小さな揺れしか経験せず、全ての対称操作が単純な幾何操作に対応している「剛体」分子を記述するために有用である。しかしながら、ロンゲ＝ヒギンズは複数の等価な構造を持つ非剛体分子について適したより一般的な種類の対称群を提唱している^[9]^[10]。これらの群は「置換-反転」群と呼ばれる。これは、対称操作が等価な核のエネルギー的に許容な置換あるいは重心に関する反転、あるいはそれら2つの組み合わせであり得るためである。

例えば、エタン（C₂H₆）は3つの等価なねじれ形配座を持つ。ある配座のもう一つの配座への変換は、1つのメチル基のもう一方のメチル基に相対的な「内部回転」によって常温で起こる。これはC₃軸に関する全分子の回転ではないが、1つのメチル基の3つの同一の水素原子の置換として記述することができる。上記の表で示されているようにそれぞれの配座はD_3d対称性を持つものの、内部回転、関連した量子状態およびエネルギー準位の記述はより完全な置換-反転群を必要とする。

同様に、アンモニア（NH₃）は2つの等価な三角錐（C_3v）配座を持ち、これらの配座は窒素反転として知られる過程によって相互変換する。NH₃は反転中心を持たないため、これは剛体分子の対称操作に対して用いられている意味での反転ではない。むしろ、この分子についてエネルギー的に許容される（窒素に近い）重心に関する全原子の鏡映である。再び、置換-反転群が2つの構造の相互作用を記述するために用いられる。

非剛体分子の対称性への2つ目の似た手法はAltmannによるものである^[11]^[12]。この手法では、対称群は「シュレーディンガー超群」と呼ばれ、(1) 剛体分子の幾何対称操作（回転、鏡映、反転）、(2) 「等力 (isodynamic) 操作」という2種類の操作（とそれらの組合せ）からなる。後者は、単結合に関する回転（エタン）あるいは分子の反転（アンモニア）といった物理学的に合理的な過程によって非剛体分子をエネルギー的に等価な形へと入れる^[12]。

脚注

^ Quantum Chemistry, Third Edition John P. Lowe, Kirk Peterson ISBN 0-12-457551-X NCID BA73748998
^ Physical Chemistry: A Molecular Approach by Donald A. McQuarrie, John D. Simon ISBN 0-935702-99-7
^ The chemical bond 2nd Ed. J.N. Murrell, S.F.A. Kettle, J.M. Tedder ISBN 0-471-99577-0 NCID BA12971474
^ Physical Chemistry P. W. Atkins ISBN 0-7167-2871-0
^ G. L. Miessler and D. A. Tarr “Inorganic Chemistry” 3rd Ed, Pearson/Prentice Hall publisher, ISBN 0-13-035471-6.
^ Group Theory and its application to the quantum mechanics of atomic spectra, E. P. Wigner, Academic Press Inc. (1959)
^ Correcting Two Long-Standing Errors in Point Group Symmetry Character Tables Randall B. Shirts J. Chem. Educ. 2007, 84, 1882. Abstract
^ Group Theory and the Vibrations of Polyatomic Molecules Jenny E. Rosenthal and G. M. Murphy Rev. Mod. Phys. 8, 317 - 346 (1936) doi:10.1103/RevModPhys.8.317
^ Longuet-Higgins, H.C. (1963). “The symmetry groups of non-rigid molecules”. Molecular Physics 6 (5): 445–460. doi:10.1080/00268976300100501.
^ Fundamentals of Molecular Symmetry by Philip R. Bunker and Per Jensen (Institute of Physics Publishing 2005) ISBN 0-7503-0941-5
^ Altmann S.L. (1977) Induced Representations in Crystals and Molecules, Academic Press
^ ^a ^b Flurry, R.L. (1980) Symmetry Groups, Prentice-Hall, ISBN 0-13-880013-8, pp.115-127

外部リンク

[1] Quantum Chemistry, Third Edition John P. Lowe, Kirk Peterson ISBN 0-12-457551-X NCID BA73748998

[2] Physical Chemistry: A Molecular Approach by Donald A. McQuarrie, John D. Simon ISBN 0-935702-99-7

[3] The chemical bond 2nd Ed. J.N. Murrell, S.F.A. Kettle, J.M. Tedder ISBN 0-471-99577-0 NCID BA12971474

[4] Physical Chemistry P. W. Atkins ISBN 0-7167-2871-0

[5] G. L. Miessler and D. A. Tarr “Inorganic Chemistry” 3rd Ed, Pearson/Prentice Hall publisher, ISBN 0-13-035471-6.

[6] Group Theory and its application to the quantum mechanics of atomic spectra, E. P. Wigner, Academic Press Inc. (1959)

[7] Correcting Two Long-Standing Errors in Point Group Symmetry Character Tables Randall B. Shirts J. Chem. Educ. 2007, 84, 1882. Abstract

[8] Group Theory and the Vibrations of Polyatomic Molecules Jenny E. Rosenthal and G. M. Murphy Rev. Mod. Phys. 8, 317 - 346 (1936) doi:10.1103/RevModPhys.8.317

[9] Longuet-Higgins, H.C. (1963). “The symmetry groups of non-rigid molecules”. Molecular Physics 6 (5): 445–460. doi:10.1080/00268976300100501.

[10] Fundamentals of Molecular Symmetry by Philip R. Bunker and Per Jensen (Institute of Physics Publishing 2005) ISBN 0-7503-0941-5

[11] Altmann S.L. (1977) Induced Representations in Crystals and Molecules, Academic Press

[Flurry-12] Flurry, R.L. (1980) Symmetry Groups, Prentice-Hall, ISBN 0-13-880013-8, pp.115-127

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

分子対称性

概念

要素

操作

点群

群論

一般的な点群

表現

指標表

歴史的背景

非剛体分子

脚注

関連項目

外部リンク