十一芒星
| 十一芒星 | |
|---|---|
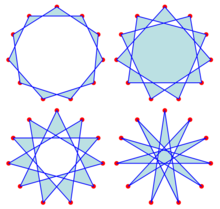 4種類の十一芒星。左上が{11/2}、右上が{11/3}、左下が{11/4}、右下が{11/5}である。 | |
| 辺・頂点 | 11 |
| シュレーフリ記号 | {11/2}, {11/3} {11/4}, {11/5} |
| コクセター図形 | |
| 対称性群 | Dih11、22通り |
| 内角 (度) | ≈114.545° {11/2} ≈81.8182° {11/3} ≈49.0909° {11/4} ≈16.3636° {11/5} |
十一芒星(じゅういちぼうせい、英語:hendecagram, endecagram, endekagram、エンデカグラム)とは、幾何学において、11個の頂点を持つ星型多角形のことである。
語源
[編集]英語において十一芒星を意味する単語である「hendecagram」は、「11」を意味する古代ギリシア語由来の倍数接頭辞である「hendeca-」と、同じく古代ギリシア語で「記録されたもの」といった意味を表す言葉に由来する接尾辞である「-gram」の合成によって成り立っている。さらに、接頭辞の「hendeca-」は古代ギリシア語で「11」を表す「ἕνδεκα」に由来する。そして、「ἕνδεκα」は、「1」を意味する「ἕν」と、「10」を意味する「δέκα」という2つの単語を合成したものである。また、接尾辞の「-gram」は、古代ギリシア語で「線」を意味する単語である「γραμμῆς」(grammēs)に由来する[1]。
正十一芒星
[編集]互いに相似でも合同でもないような正十一芒星(せいじゅういちぼうせい)は全部で4種類存在する[2]。それぞれの正十一芒星は、シュレーフリ記号を用いると、{11/2}、{11/3}、 {11/4}、{11/5}のように表記される。この表記においては、スラッシュ(/)の後の数字は辺によって接続されている頂点の組の間にある、他の辺との交点の数を示している。これらと同様の4種類の正十一芒星は、正十一角形を星型化したものとみなすこともできる[3]。
11は素数であることから、全ての十一芒星は星型多角形であり、複合的な図形になることはない。
作図
[編集]頂点の数が奇数でありかつ、フェルマー素数ではない奇数の素因数をもつ他の全ての正多角形並びに星型正多角形と同様に、正十一芒星は定規とコンパスのみを用いて作図することはできない[4]。しかしながら、Hilton & Pedersen (1986)により、長方形の紙を折ることによって、4種類の正十一芒星のうち、{11/3}、{11/4}、{11/5}の3種類については作図することが可能であることが証明され、その方法が説明されている[5]。
人工物・自然物に見られる十一芒星
[編集]
正十一芒星({11/3}もしくは{11/4})の上にあるプリズムは、デオキシリボ核酸(DNA)の構造を説明する際に、そのおおよその形として言及されることがある[6]。

2021年現在ではアメリカ合衆国のニューヨーク市にある自由の女神の土台となっているフォート・ウッドと呼ばれる星形要塞は、正十一芒星ではない十一芒星の形をしている[7]。
トプカリ絵巻には、イスラム美術において使われる十一芒星のギリー (模様)が含まれている。この絵巻に含まれている十一芒星は標準的な十一芒星の形の一つにはなっていないが、その代わりに十一角形の頂点と、それとはほぼ反対側にある十一角形の辺の中点とを結ぶ線分を用いている[8]。十一芒星のギリーの模様はアゼルバイジャンにあるモミネ・ハトゥン廟においても使われている。エリック・ブルーグは自身の著書において、この模様について「イスラーム美術の幾何学的なデザインの中でも、最高のものであるとみなせるかもしれない」と書いている[9]。
スペースシャトル固体燃料補助ロケットの先端部分の中心部(空洞になっており、この内部で燃料が燃焼する)の断面は、十一芒星の形をしていた。このようなデザインによって、表面積は大きくなり、打ち上げの初期段階における推力も大きくなった。また、同じ時間に消費する燃料が少なくて済むようになった。さらに、ロケットの速度が音速の壁を超えたのとほぼ同じタイミングでスターポイントが燃え尽きた後の推力も小さくなった[10]。
また、インスタグラムにおいては、青の正十一芒星が、認証されたページを区別するために使用されている。
関連項目
[編集]脚注
[編集]- ^ Liddell, Henry George; Scott, Robert (1940), A Greek-English Lexicon: γραμμή, Oxford: Clarendon Press
- ^ O'Daffer, Phares G.; Clemens, Stanley R. (1976), Geometry: an investigative approach, Addison-Wesley, Exercise 7, p. 62, ISBN 9780201054200.
- ^ Agricola, Ilka; Friedrich, Thomas (2008), Elementary Geometry, Student mathematical library, 43, American Mathematical Society, p. 96, ISBN 9780821890677.
- ^ Carstensen, Celine; Fine, Benjamin; Rosenberger, Gerhard (2011), Abstract Algebra: Applications to Galois Theory, Algebraic Geometry, and Cryptography, Sigma series in pure mathematics, 11, De Gruyter, p. 88, ISBN 9783110250084, "On the other hand a regular 11-gon is not constructible."
- ^ Hilton, Peter; Pedersen, Jean (1986), “Symmetry in mathematics”, Computers & Mathematics with Applications 12 (1-2): 315–328, doi:10.1016/0898-1221(86)90157-4, MR838152
- ^ Janner, Aloysio (June 2001), “DNA enclosing forms from scaled growth forms of snow crystals”, Crystal Engineering 4 (2–3): 119–129, doi:10.1016/S1463-0184(01)00005-3
- ^ Adams, Arthur G. (1996), The Hudson River Guidebook, Fordham Univ Press, p. 66, ISBN 9780823216796.
- ^ Bodner, B. Lynn (2009), “The eleven–pointed star polygon design of the Topkapı Scroll”, Bridges 2009: Mathematics, Music, Art, Architecture, Culture, pp. 147–154.
- ^ Broug, Eric (2013), Islamic Geometric Design, Thames & Hudson, p. 182
- ^ Angelo, Joseph A. (2009), Encyclopedia of Space and Astronomy, Infobase Publishing, p. 511, ISBN 9781438110189.
外部リンク
[編集]- Weisstein, Eric W. "Polygram". mathworld.wolfram.com (英語).