確率測度
| 確率論 |
|---|
 |

確率論における確率測度(かくりつそくど、英: probability measure)は、標本空間に事象となる完全加法族が与えられたとき、事象の確率を測る測度のことである。一般の測度の公理(完全加法性など)に加えて、標本空間の測度は 1 であることが公理に加わる[3]。
確率測度は、アンドレイ・コルモゴロフが『確率論の基礎概念』(1933年)[4]で確率を公理的確率へと拡張する上で導入された。
確率を「事象の測度」ととらえることにより、確率を公理的立場から決定し、非等確率空間における理論的確率も求められるようになった。
確率測度は物理学からファイナンスや生物学まで様々な分野において応用されている。
導出の必然性
[編集]根元事象が無数にある場合は確率をラプラスの古典的確率で定義することができない。また、アンドレイ・コルモゴロフは自身が見出した定理(コルモゴロフの拡張定理)により、確率を無限次元に対して拡張できる必要十分条件として、確率関数がσ-加法性を満たすことを見出し、測度としての公理的確率を提唱した。
定義
[編集]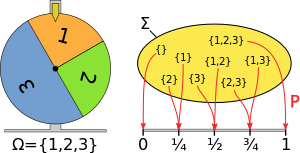
函数 μ が事象空間上の確率測度であるためには、以下の2つの条件が満たされなければならない。
-
- を満たす(完全加法性、英: countable additivity)。
例えば、確率変数 X が 1, 2, 3 を取る確率がそれぞれ 1/4, 1/4, 1/2 であるとすると、X = 1 or 3 である確率は 1/4 + 1/2 である。
事象の共通部分に基づく条件付き確率は以下のように定義される。
このような条件付き確率は、P(A) が 0 でない限り、確率測度である[5]。
より一般的なファジー測度は確率測度とは異なるものになっている。ファジー測度では、ファジー値を足し上げた時に 1 とはならないかもしれない。そして、加法性は集合の包含関係に基いた順序関係に置き換えられる。
応用例
[編集]実際の金融の動きに基づいた金融市場の空間へ確率を割り当てたマーケット測度 (英: Market measures) は、確率測度の例である。この例は、デリバティブの価格付けなどの、数理ファイナンスにおいて関心が高い[6]。例えば、リスク中立測度は、金融資産の将来のペイオフを利子率で割り引いた値の、リスク中立測度に基づいた(つまり、対応するリスク中立密度関数を使い計算された)期待値が、その資産の現在価格となるような確率測度である。このようなリスク中立測度が一意に存在する場合、そのような金融市場を完備市場と呼ぶ[7][8]。
直観的な意味でチャンスや可能性を表す測度の全てが確率測度であるとは言えない。例えば、統計力学の系の基本的な考え方は測度空間ではあるが、測度がいつも確率測度であるわけではない[1]。一般に、統計物理学では、もし「状態 A であるような系 S の確率は p である」という形の文章を考えたならば、自由度が1つの系の場合には確率測度が定義できるように思えるが、系の幾何学が合同関係 (congruence) の下での確率測度を常に定義するわけではない[2]。
確率測度は、数理生物学でも使われる[9]。例えば、比較配列分析(sequence analysis)において、確率測度は配列の中にアミノ酸がある可能性によって定義されることもある[10]。
参照項目
[編集]参考文献
[編集]- ^ a b A course in mathematics for students of physics, Volume 2 by Paul Bamberg, Shlomo Sternberg 1991 ISBN 0-521-40650-1 page 802
- ^ a b The concept of probability in statistical physics by Yair M. Guttmann 1999 ISBN 0-521-62128-3 page 149
- ^ An introduction to measure-theoretic probability by George G. Roussas 2004 ISBN 0-12-599022-7 page 47
- ^ アンドレイ・コルモゴロフ 著、坂本實 訳『確率論の基礎概念』筑摩書房〈ちくま学芸文庫 [Math & science]〉、2010年7月7日。ISBN 978-4-480-09303-5。
- ^ Probability, Random Processes, and Ergodic Properties by Robert M. Gray 2009 ISBN 1-4419-1089-1 page 163
- ^ Quantitative methods in derivatives pricing by Domingo Tavella 2002 ISBN 0-471-39447-5 page 11
- ^ Irreversible decisions under uncertainty by Svetlana I. Boyarchenko, Serge Levendorskiĭ 2007 ISBN 3-540-73745-6 page 11
- ^ アセットプライシングの基本定理を参照。
- ^ Mathematical Methods in Biology by J. David Logan, William R. Wolesensky 2009 ISBN 0-470-52587-8 page 195
- ^ Discovering biomolecular mechanisms with computational biology by Frank Eisenhaber 2006 ISBN 0-387-34527-2 page 127
さらに先の文献
[編集]- Probability and Measure by Patrick Billingsley, 1995 John Wiley ISBN 978-0-471-00710-4
- Probability & Measure Theory by Robert B. Ash, Catherine A. Doléans-Dade 1999 Academic Press ISBN 0-12-065202-1

