第一原理的手法 (原子核物理学)
| 原子核物理学 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
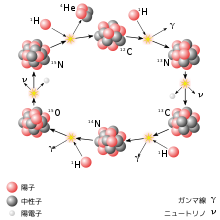
| ||||||||||||||
| 放射性崩壊 核分裂反応 原子核融合 | ||||||||||||||
| ||||||||||||||
原子核物理学において第一原理的手法(だいいちげんりてきしゅほう)とは、原子核を構成する核子とその間に働く力についての非相対論的シュレディンガー方程式を解くことで原子核について一から記述することを目的とする手法のことである。例えば殻模型などと比較すると、これはより根本的なアプローチであるといえる。以前は極めて軽い原子核のみの取り扱うに留まっていたが、近年の研究の発展によりニッケルなどのより重い原子核を取り扱えるようになった[1]。
第一原理的取り扱いにおいて顕著に困難な点は、核子間相互作用の複雑性によるものである。強い相互作用は量子色力学(QCD)により記述される核力に起因すると考えられているが、原子核物理で扱う低エネルギー領域ではQCDは非摂動的であるため、QCD を核子間相互作用の記述に直接的に用いることは非常に困難であり (格子QCD参照)、何らかのモデルを代わりに用いる必要がある。利用可能な最も洗練されたモデルはカイラル有効場の理論(EFT)に基づくモデルである。この有効場の理論には QCD の対称性に矛盾しないあらゆる相互作用が含まれる。QCD における自由度はクォークおよびグルーオンであるのと対照的に、この理論の自由度は核子とパイ中間子である。有効場の理論には低エネルギー定数とよばれるパラメータが含まれ、これは散乱データから決定される[1][2]。
カイラルEFT は多体力、特に原子核の多体問題において本質的な要素のひとつとされる三核子間相互作用の存在を示唆する[1][2]。
ハミルトニアン (カイラル摂動論や他の手法に基づく) を得ると、シュレディンガー方程式を解かねばならない。
ここで は 原子核中のA個の核子の多体波動関数である。この方程式を数値的に解くために種々の第一原理的手法が考案されてきた。
- グリーン関数モンテカルロ法 (GFMC)[3]
- No-core shell model (NCSM)[4]
- 結合クラスター法 (CC)[5]
- 自己無撞着グリーン関数 (SCGF)[6]
- In-medium similarity renormalization group (IM-SRG)[7]
発展資料
[編集]- Dean, D. (2007). “Beyond the nuclear shell model”. Physics Today 60 (11): 48. doi:10.1063/1.2812123.
- Zastrow, M. (2017). “In search for “magic” nuclei, theory catches up to experiments”. Proc Natl Acad Sci U S A. 114 (20): 5060-5062. doi:10.1073/pnas.1703620114.
脚注
[編集]- ^ a b Machleidt, R.; Entem, D.R. (2011). “Chiral effective field theory and nuclear forces”. Physics Reports 503 (1): 1–75. arXiv:1105.2919v1. Bibcode: 2011PhR...503....1M. doi:10.1016/j.physrep.2011.02.001.
- ^ Pieper, S.C.; Wiringa, R.B. (2001). “Quantum Monte Carlo calculations of light nuclei”. Annual Review of Nuclear and Particle Science 51: 53-90. doi:10.1146/annurev.nucl.51.101701.132506.
- ^ Barrett, B.R.; Navrátil, P.; Vary, J.P. (2013). “Ab initio no core shell model”. Progress in Particle and Nuclear Physics 69: 131–181. doi:10.1016/j.ppnp.2012.10.003.
- ^ Hagen, G.; Papenbrock, T.; Hjorth-Jensen, M.; Dean, D. J. (2014). “Coupled-cluster computations of atomic nuclei”. Reports on Progress in Physics 77 (9): 096302. doi:10.1088/0034-4885/77/9/096302.
- ^ Cipollone, A.; Barbieri, C.; Navrátil, P. (2013). “Isotopic Chains Around Oxygen from Evolved Chiral Two- and Three-Nucleon Interactions”. Phys. Rev. Lett. 111 (6): 062501. doi:10.1103/PhysRevLett.111.062501.
- ^ Hergert, H.; Binder, S.; Calci, A.; Langhammer, J.; Roth, R. (2013). “Ab Initio Calculations of Even Oxygen Isotopes with Chiral Two-Plus-Three-Nucleon Interactions”. Phys. Rev. Lett. 110 (24): 242501. doi:10.1103/PhysRevLett.110.242501.


