経済成長の黄金律

黄金律のイメージ

経済成長の黄金律（けいざいせいちょうのおうごんりつ）は、一定の成長率で進む経済成長のうちで、消費が最も多い経済成長である^[1]。黄金則とも訳す^[2]。

エドムンド・フェルプスの寓話は、むかしむかしソロヴィア王国の百姓オイコ・ノモスが黄金律を思いつきました、という筋書きだが^[3]、本当は1960年代の初めにフェルプスをふくむ数人の経済学者がそれぞれ独自に黄金律を発案した^[4]。フェルプスらの定理によると、利子率が成長率に等しいのが黄金律である^[5]。

黄金律では資本が稼いだ収益を全て投資して蓄積する。このことを蓄積の黄金律^[6]とも資本蓄積の黄金律^[7]ともいう。黄金律では資本収益を全て再投資しないといけないので、資本を所有するだけの不労所得生活者は何も消費できない^[8]。黄金律の実現は経済の成熟を示す^[9]。

黄金律は単純なので分かりやすい^[10]。最適成長理論の基本中の基本とされる^[9]。政策当局は黄金律に魅せられて、黄金律をめざしたいと思うことがあるという^[10]。

概要

均斉成長（黄金時代）

1961年に黄金律を提唱したフェルプスは、全ての経済変数がそれぞれ一定の成長率で伸びてゆく経済成長を黄金時代とよんだ^[11]。

1920年代のジョーン。これよりおよそ30年後に黄金時代を定義する。

この黄金時代の概念は1956年にジョーン・ロビンソンが定義した^[12]。現実には経済が厳密に一定の伸び率で成長しつづけることはないので、黄金時代という言葉には「実現しそうにない神話的な状態」という意味がこめられていた^[13]。もともと黄金時代はギリシア神話上の時代区分のひとつであり、最も古く長くつづいた時代であったとされる^[14]。フェルプスが黄金律を提唱したときの寓話は、古代ギリシア風の架空の王国を舞台とし、その主人公は古代ギリシア語の「経済」をモジったオイコ・ノモスという名であった^[3]。

黄金律が提唱された当時は経済学で黄金時代という言葉がつかわれていた^[15]。現在は経済学で黄金時代という言葉をつかうことはほとんどなく、そのかわりに均斉成長という^[16]。これを恒常状態ともいうが^[17]、経済学者によっては成長率がゼロの場合に限ってこれを恒常状態とよぶことがあるというので気をつける^[18]。

黄金律が提唱される少し前、ニコラス・カルドアは経済統計を観察し、現実の経済成長がおおむね均斉成長であるという事実を発見した^[19]。カルドアはこれを定型化された事実（英語版）とよび、黄金律が提唱された年と同じ1961年に公表した^[20]。現代の経済成長理論でも、均斉成長は現実を要約して記述する概念として有益であると考えられている^[21]。

均斉成長における技術進歩は資本の生産効率を高めずに労働の生産効率を高めるかのようなかたちになる^[22]。これを労働拡張型技術進歩という。このことは、1961年に宇沢弘文が発表した論文で証明された（宇沢の定理）。これと同じ1961年に黄金律を提唱したフェルプスは、初めこのことに気づいていなかったが、1965年の第二論文でこれを取りいれた^[23]。

黄金律

均斉成長（黄金時代）は成長率が一定であるというだけで、それ自体が望ましいというわけではない。一方、フェルプスは、黄金時代（ゴールデン・エイジ）で望ましいルールを黄金律（ゴールデン・ルール）とよんだ^[3]。黄金律は消費を最大化する黄金時代（均斉成長）と定義される^[4]。

黄金律で最大化されるのは消費であって、生産や所得が最大化されるわけではない。政策評価や経済分析の実務では国内総生産や国民所得で豊かさを測るが、経済学では消費で豊かさを評価する^[24]。

1984年のフェルプス。この23年前に黄金律を提唱した。

黄金律の定理によると、資本収益率（利子率）が成長率に等しくなる均斉成長が存在する場合、その均斉成長が消費を最大化する黄金律である^[4]。この定理を言葉で説明すると次のとおりである。資本を増やしたうえで成長率一定の均斉成長をたもつと、資本が増えたことで生産が増えて消費が増えるが、その一方で、均斉成長をたもつには資本への再投資を増やさないといけないので、その再投資の分だけ消費が減ってしまう。すると、増産で消費の増える分と、再投資で消費の減る分とがバランスするところがあれば、そこで消費が最大化される。そして、資本の増えた分に資本収益率をかけた分だけ生産が増え、また、資本の増えた分に成長率をかけた分だけ再投資しないと均斉成長をたもてないことがわかっている。これらを考えあわせると、資本収益率と成長率がバランスするところが、増産で消費の増える分と再投資で消費の減る分がバランスするところであり、そこが消費を最大化する黄金律である。つまり資本収益率と成長率が等しくなるところが黄金律である。以上について数式をもちいた説明は黄金律の定理の節を参照。

黄金律のアイデアは1947年にモーリス・アレがフランス語で著した本にさかのぼるといわれるが、黄金律の名で広く知られるようになったは、1961年にフェルプスが寓話のかたちのペーパー^[3]をアメリカン・エコノミック・レビュー誌で発表してからである^[25]。その後フェルプスは1965年に同誌で第二論文^[4]を発表し、1966年に著書『経済成長の黄金律』^[26]を刊行した。この間、黄金律と同様のアイデアは、モーリス・アレやジョーン・ロビンソン、トレイヴァー・スワン（英語版）、カール・クリスティアン・フォン・ヴァイツゼッカー（ドイツ語版）、ジャック・デルソー（フランス語版）によっても発表された^[27]。

2006年フェルプスがノーベル経済学賞を受賞した際、フェルプスの業績の一つに黄金律に関する研究が挙げられた^[25]。

黄金律貯蓄率

フェルプスの寓話はソロヴィア王国を舞台とする^[3]。ソロヴィア王国という国名はフェルプスの同僚学者ロバート・ソローの姓をモジったものであり、ソローの成長モデルは貯蓄率 s を一定と仮定するモデルであった^[28]。フェルプスが初めて黄金律を提唱したとき、ソロヴィア王国の人びとは単純なので生産物の一定割合 s を蓄積するものと仮定して、s の中から消費を最大化する黄金律をえらぶという考え方をしていた^[3]。この考え方によると、黄金律では、資本収益の所得に占める割合と s が等しくなるという関係が成りたつ^[3]。この関係をフェルプスは蓄積の黄金律とよんだ^[6]。資本蓄積の黄金律ともよばれる^[7]。

このように s を一定と仮定して導いた黄金律の s を黄金律貯蓄率という^[29]。フェルプスは1965年の第二論文以降、s を一定を仮定することはなく、均斉成長で結果として s が一定になることを導いている^[4]。

最適成長理論

世界銀行レポート『黄金成長』によると、黄金律は最適成長理論で最も基本的な命題であると今も多くの経済学者が考えているという^[9]。また、ある学術博士はブログで、最適成長理論は無限の未来の消費を最大化する、これが黄金律なのだ、というようなことを書いている^[30]。しかし、以下で述べるように、最適成長理論における黄金律の位置づけはそれほど簡単なものではない。

黄金律に向かう道すじ

2008年時点のフェルプスは黄金律を目指すのが最適といえないと認めているが^[31]、1961年に黄金律を提唱した当初のフェルプスは黄金律を望ましいものとして扱っていた^[3]。この場合、すでに黄金律に達しているときは黄金律をたもてばいいが、黄金律から外れているときはどのような道すじで黄金律に向かえばいいかという問題がある。この問題についてフェルプスは、寓話の主人公オイコ・ノモスに次のように主張させている^[32]（意訳）。

何としてでも今後ずっと確実に黄金律の道すじを進むべきです。黄金律では資本と生産の比率が決まっています。今の資本生産比率が黄金律より低ければ、その不足分がなくなるまで消費を先送りすべきです。今の資本生産比率が黄金律を超えていれば、その超過分がなくなるまで消費を前倒しすべきです。ひとたび黄金律に到達したら、そのあとは黄金律で投資することを皆で誓わなくてはいけません。黄金律にしたがって投資比率を収益比率と一致させてゆけば、後で悔やむことにならないでしょう。こうして最適に準じる社会投資政策の基礎ができあがるのです。

いそいで黄金律を達成すべきだというのがオイコ・ノモスの主張だが、最後で「最適に準じる」と語らせているあたり、この主張の甘さをフェルプス自身が認めていることを表わしている^[33]。厳密な理論を構成するためには、何が最適であるかを厳密に定める必要がある^[33]。フェルプスの寓話の筋書きは、数学者たちが最適をもとめて極値問題や汎函数やハミルトニアンに取りくみました、しかし実現できる答えを出せませんでした、そこで大がかりな最適化問題を忘れて単純に考えることになりました、そして賢い百姓オイコ・ノモスが黄金律を思いつきました、という話しであった^[34]。経済成長の最適化問題は、フェルプスが寓話を発表したあと、次に述べる最適成長モデルで解かれる。

最適成長モデル

最適成長モデルの位相図。青い線が均斉成長に向かう最適な道すじを示す鞍点経路である。kとcの間には、新古典派成長モデルの節で示す関係があり、時間の経過とともに矢印の方向に変化する。k不変の曲線上のcの最大点が黄金律。均斉成長のcやkは黄金律より低い。

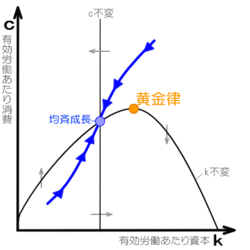
1960年代、フェルプスらの黄金律の研究と並行して、デイヴィッド・キャスやチャリング・クープマンスが最適成長モデルをつくりあげた^[35]。最適成長モデルは経済の進むべき望ましい道すじを一本えらぶ。その結果は、望ましい道すじの先にある均斉成長において、資本収益率が成長率を上まわり、消費が黄金律より少なくなる。

最適成長モデルが黄金律に達しないわけは、黄金律に達すると社会厚生（英語版）が無限になってしまって都合がわるいからである^[36]。このことを説明すると次のとおりである。最適成長モデルは、人々の日々の消費を数値で評価し、その数値を無限の未来まで積みあげて社会厚生を計算し、その社会厚生を最大にするように、経済の進むべき道すじを一本えらぶ。日々の消費を評価するにあたっては、未来を先にゆけばゆくほど日々の消費を割り引いて評価する。これは、目先の消費を優先して、先ゆきの消費を犠牲にする傾向があるということなので、長い目でみると消費が黄金律より少なくなる。先ゆきの消費をあまり割り引かないようにすれば長い目でみて消費は増えるが、そうして消費を増やして黄金律に近づけてゆくと、社会厚生が無限大になってしまう。社会厚生が無限大というのは素晴らしいことのように思えるが、無限大のまわりどれも無限大なので、一本の道すじをえらべない。道すじを一本えらべるようにすると黄金律に達しない。いいかえると、道すじを一本えらぶ最適成長モデルは黄金律をえらばない。

動学非効率性

黄金律が最適成長モデルでえらばれないという点に関して、フェルプスは、その場合でも黄金律は動学非効率性の境界線として規範的な意義をもつと主張した^[4]。動学非効率性というのは、消費を一方的に増やせる機会があるのに、その機会を活かしていないという意味で無駄のある状況をいう。資本が黄金律を超えるほど余分に蓄積され、資本収益率が成長率を下まわるほど低下すると動学非効率におちいる。

現代の経済成長理論において黄金律貯蓄率は、きちんと定義された選好から導かれたものではないので最適性の観点からみると過去の遺物とみなされるが、そうであっても動学効率性の議論で役に立つとされる^[37]。動学非効率性の文脈において「蓄積の黄金律は今も最適成長理論で最も基本の命題である」といわれる^[38]。

たとえばグレゴリー・マンキューはトマ・ピケティ『21世紀の資本』を批判するペーパーで、動学非効率性の境界線として黄金律に言及している^[39]。批判されたピケティも実は『21世紀の資本』の目立たない場所で黄金律が動学非効率性の境界線になることを論じていた^[40]。ピケティは歴史データをもとに資本収益率 r が経済成長率 g を平均的に上まわるという不等式 r > g を見いだし、それを根拠にして、現実経済の動学非効率性を否定した^[41]。かつてマンキューは、もっと緻密な実証方法で先進国の動学非効率性を否定する結果をえたことがあった^[42]。

市場経済と黄金律

修正黄金律

もともと最適成長モデルは望ましい経済成長をえらぶためのものであったが、今はこれを市場経済のカリカチュアに使いまわす^[43]。これを新古典派成長モデル^[44]とか標準的新古典派モデル^[43]、あるいはラムゼイ・モデル^[45]という。

新古典派成長モデルは、均斉成長で利子率が成長率を上まわり、消費が黄金律より少なくなる^[46]。新古典派成長モデルが黄金律に達しないことを修正黄金律ということがある^[47]。また、均斉成長の利子率を決定する数式を修正黄金律ということがある^[48]。これを変形黄金則と訳すこともある^[49]。

新古典派成長モデルが黄金律に達しないわけは、黄金律に達するようにすると家計効用が無限大になってしまって都合がわるいからである^[50]。このことを言葉で説明すると、最適成長モデルのときの説明をほぼ繰りかえすことになるが、次のとおりである。新古典派成長モデルでは、永久に存続する家計が無限の未来を見とおして、日々の消費を数値で評価して、これを無限の未来まで積みあげて家計効用を計算し、その家計効用を最大にするように消費行動をえらぶ。日々の消費を評価するにあたっては、未来を先にゆけばゆくほど日々の消費を割り引いて評価する。これは、目先の消費を優先して、先ゆきの消費を犠牲にするということなので、長い目でみると消費が黄金律より少なくなる。先ゆきの消費をあまり割り引かないようにしてゆけば長い目でみて消費は増えるが、そうして消費を増やしていって黄金律に近づけてゆくと、家計効用が無限大になってしまう。無限大にならない程度にきつく割り引くようにする必要があるが、そうすると黄金律に達しない。以上について数式をもちいた説明は新古典派成長モデルの節を参照されたい。

国債発行

2010年のダイアモンド。この45年前、国債発行で黄金律を達成する理論を示した。

資本が黄金律を超えて蓄積されて消費が黄金律より少なくなる場合、政府は国債を十分に発行することで黄金律を達成できる^[51]。そのわけは次のとおりである。現役世代は老後にそなえて貯蓄し、老後は貯蓄を取り崩して消費するという世代重複モデル（英語版）を考える。現役世代が老後の生活を心配するあまり貯蓄しすぎると、資本が黄金律を超えるほど余分に蓄積される場合がある。その場合、政府が国債を十分に発行し、現役世代が国債で貯蓄すれば、貯蓄が余分な資本蓄積にまわらなくなり、その分消費が増えて黄金律が達成される。

この理論は1947年にモーリス・アレがフランス語で著した本にさかのぼるといわれるが、アレとは別にピーター・ダイアモンドが1965年にアメリカン・エコノミック・レビュー誌で発表した^[52]。このことはダイアモンドがノーベル経済学賞を受賞した際、その業績の一つに数えられている^[52]。

合理的バブル

2007年のティロール。この22年前にバブル均衡で黄金律が成りたつ理論を示した。

資本が黄金律を超えて蓄積されて消費が黄金律より少なくなる場合、合理的バブルが発生する可能性があり、合理的バブルが均斉成長で存続すると黄金律が達成される^[53]。そのロジックは、ダイアモンドの世代重複モデルにおける国債を合理的バブルにおきかえたものであり、次のように考える。

1. 資本が黄金律を超えるほど余分に蓄積され、資本収益率が成長率を下まわるほど低下すると、低収益の資本に投資するぐらいならバブルに賭けてみるのが合理的になる。そうして発生する合理的バブルの収益率は資本収益率と一致する。そのわけは、バブルの収益率が資本収益率より低ければバブルを売って資本を買えば儲かるし、バブルの収益率が資本収益率より高ければ資本を売ってバブルを買えば儲かるが、こうした裁定取引が十分に行われると収益率の違いがなくなるからである。
2. バブルというのは、本来無用の物でありながら、ただ値上がりするから買われ、ただ買われるから値上がりする。その性質上、バブルの膨張率はそのままバブルの収益率になる。
3. バブルがうまい具合に存続するような均斉成長をバブル均衡という。バブル均衡でバブルは経済成長率と同じ伸び率で膨張する。

まとめると、1.資本収益率は裁定取引によりバブル収益率と一致し、2.バブル収益率は性質上バブル膨張率に一致し、3.バブル膨張率はバブル均衡で経済成長率と一致する。つまりバブル均衡で資本収益率と成長率が一致する。このことはバブル均衡が黄金律であることを示す。

この合理的バブルの理論は1985年にジャン・ティロールがエコノメトリカ誌で発表した^[53]。この理論はティロールがノーベル記念経済学賞を受賞した際、その業績の一つに数えられている^[54]

近年の論調

世界銀行『黄金成長』

世界銀行が2012年に発行したレポート『黄金成長：ヨーロッパ経済モデルの輝きを取りもどす』は、黄金律にインスピレーションを得てタイトルをつけ、黄金律にもとづいて政策提言をおこなっている^[9]。

このレポートによると、黄金律は最適成長理論で最も基本的な命題であると今も多くの経済学者が考えている^[9]。黄金律をたもつことは経済の成熟をしめす^[9]。黄金律は単純なので分かりやすく、政策当局は黄金律に魅せられてこれをめざしたいと思うことがあるという^[10]。

ピケティ『21世紀の資本』

2015年のピケティ。黄金律に否定的。

トマ・ピケティは、2013年にフランス語で著し2014年に日本語に翻訳された『21世紀の資本』で、黄金律について次のような自説を展開している。およそ黄金律に対して否定的である。

• 歴史データをみると資本収益率が成長率よりずっと高いので、現実の資本は黄金律よりずっと少ない^[55]。現実経済が黄金律ほどの資本を蓄積するとは考えにくい^[56]。黄金律は抽象理論にすぎず実際問題であまり役に立たない^[56]。
• 黄金律において、資本を所有する不労所得生活者は、資本の収益の全てを再投資しないと自分の地位を保てないので、何も消費できない^[56]。したがって黄金律の実現は不労所得生活者の支配を終わらせる^[57]。しかし黄金律を無理に実現する必要はなく、そうするよりも不労所得生活者に課税するほうがずっと簡単で効果的だ^[57]。
• 黄金律は資本の上限を設定するだけのものであって、黄金律に到達するのが望ましいという主張を導き出すものではない^[57]。目先の消費を犠牲にしてまで先ゆきの黄金律をめざすのが適切とは限らない^[58]。

なお、以上のような議論でピケティは均斉成長を基準に考えている^[59]。均斉成長では資本と生産が同じ伸び率で成長することが知られる^[22]（宇沢の定理）。一方、ピケティは『21世紀の資本』の「おわりに」で資本が生産より速く急成長すると主張している^[60]。グレゴリー・マンキューはこれを批判して、ピケティのいうような成長は均斉成長から外れてゆくが、標準的な成長理論は均斉成長を基準にして考えるので、ピケティの考えは標準的理論から外れていると指摘した^[39]。

語源説

経済成長の黄金律は聖書の黄金律に由来するという説がある。この説によると、経済成長の黄金律の語源は、新約聖書マタイ伝にある黄金律「人にしてもらいたいと思うことは、あなたがたも人にしなさい」に由来し、これを経済用語におきかえると「現代の世代にも未来の世代にも同じだけ消費させる場合、あるいは、未来の世代の消費を自分たちの消費より少なくしない場合、一人当たり消費の最大量は黄金律である」と解釈できるから、黄金律と名づけられたのだという^[61]。また一説には、新約聖書ルカ伝第6章31節にある黄金律を世代間の関係に拡張したものなのだともいう^[62]。

もっとも、フェルプスが黄金律を命名したとき、黄金時代（ゴールデン・エイジ）のルールを黄金律（ゴールデン・ルール）と名づけたのであって、語源を聖書の黄金律に求めていない^[3]。後にフェルプスは次のように語っている^[31]。

黄金律という言葉はダジャレ（a play on words）であった。ロビンソン夫人が定常成長の状態を黄金時代と命名したので、黄金時代の選択に関する命題を黄金律と呼ぶのは当然であった。これにくわえて、この言葉の裏に聖書の黄金律「あなたが他人にしてほしいことを他人にしなさい」をほのめかした。

そしてフェルプスは、聖書の黄金律について、他人に権利を要求する者は同じ権利を他人に与えなければならないという意味と解釈する。この意味での黄金律にしたがうと、各世代は前の世代に要求する貯蓄政策を次世代のために自ら実践しなければならない。世代をまたいだ貯蓄政策を選ぶにあたっては、生産や資本収益などに対して一定の線形関係のかたちであらわされる貯蓄政策の中から選ぶ必要がある。さもなければ、各世代は前の世代に貯蓄を要求する一方で、自分は貯蓄を減らしてしまう、という^[31]。

数式をもちいた説明

宇沢の定理

変数がそれぞれ一定の伸び率で成長する均斉成長において、技術進歩は労働拡張型である。この定理は初めジョーン・ロビンソンが図示し^[63]、1961年に宇沢弘文が証明した^[64]。これを宇沢の定理という^[65]。

宇沢の定理について、証明方法を簡素化した Schlicht (2006)にもとづいて数式をつかって示すと以下のとおりである^[66]。

宇沢の定理では、次のような経済構造を考える。

1. ${\displaystyle Y_{t}=F(K_{t},L_{t};t)}$　…時点 ${\displaystyle t}$ の生産物 ${\displaystyle Y_{t}}$ は生産関数 ${\displaystyle F}$ をつうじて資本 ${\displaystyle K_{t}}$ と労働投入 ${\displaystyle L_{t}}$ によってつくられる。関数 ${\displaystyle F}$ は資本 ${\displaystyle K_{t}}$ と有効労働 ${\displaystyle L_{t}}$ に関して１次同次関数とする（規模に関して収穫一定）。関数中の最後の項「${\displaystyle ;t}$」は時点 ${\displaystyle t}$ が進むにしたがって生産関数が変化することを示す。
2. ${\displaystyle Y_{t}=C_{t}+I_{t}}$　…生産物 ${\displaystyle Y_{t}}$ は消費 ${\displaystyle C_{t}}$ にあてられるか投資 ${\displaystyle I_{t}}$ にあてられる。
3. ${\displaystyle {\dot {K_{t}}}=I_{t}-\delta K_{t}}$　…資本 ${\displaystyle K_{t}}$ は投資 ${\displaystyle I_{t}}$ によって増えるが、一定の減耗率 ${\displaystyle \delta }$ で減る。

以上の経済構造のもとで、${\displaystyle X\in \{Y,K,L,C,I\}}$について、各変数${\displaystyle X_{t}>0}$ は一定の率 ${\displaystyle g_{X}}$ で成長する、すなわち${\displaystyle X_{t}=X_{0}e^{g_{X}t}}$とする。これを時間微分すると${\displaystyle {\dot {X_{t}}}=g_{X}X_{t}}$である。

均斉成長で生産と資本の成長率が一致することを以下のとおり示す。

まず、${\displaystyle g_{Y}=g_{I}}$を次のように導く。${\displaystyle {\dot {X_{t}}}=g_{X}X_{t}}$をもちいて、次の式1の時間微分から式2を得て、またその時間微分から式3を得る。

1. ${\displaystyle Y_{t}=C_{t}+I_{t}}$
2. ${\displaystyle g_{Y}Y_{t}=g_{C}C_{t}+g_{I}I_{t}}$
3. ${\displaystyle g_{Y}^{2}Y_{t}=g_{C}^{2}C_{t}+g_{I}^{2}I_{t}}$

これらを適宜代入して

1. ${\displaystyle (g_{Y}-g_{I})(g_{Y}-g_{C})Y_{t}=0}$
2. ${\displaystyle (g_{Y}-g_{I})(g_{C}-g_{I})I_{t}=0}$

を得る。${\displaystyle Y_{t}>0,I_{t}>0}$であるから

1. ${\displaystyle g_{Y}=g_{I}}$ または ${\displaystyle g_{Y}=g_{C}}$、かつ
2. ${\displaystyle g_{Y}=g_{I}}$ または ${\displaystyle g_{C}=g_{I}}$

である。ここで${\displaystyle g_{Y}\neq g_{I}}$を仮定すると、上記1から ${\displaystyle g_{Y}=g_{C}}$ 、上記2から ${\displaystyle g_{C}=g_{I}}$ になるので、${\displaystyle g_{Y}=g_{C}=g_{I}}$になるが、これは${\displaystyle g_{Y}\neq g_{I}}$の仮定と矛盾する。背理法により${\displaystyle g_{Y}=g_{I}}$であることがわかる。

また、${\displaystyle g_{I}=g_{K}}$を次のように導く。${\displaystyle {\dot {K_{t}}}=g_{K}K_{t}}$を${\displaystyle {\dot {K_{t}}}=I_{t}-{\delta }K_{t}}$に代入して次の式1を得て、またその時間微分から次の式2を得る。

1. ${\displaystyle g_{K}K_{t}=I_{t}-{\delta }K_{t}}$
2. ${\displaystyle g_{K}^{2}K_{t}=g_{I}I_{t}-g_{K}{\delta }K_{t}}$

これらから ${\displaystyle K_{t}}$ を消去して${\displaystyle (g_{I}-g_{K})I_{I}=0}$を得る。${\displaystyle I_{t}>0}$であるから${\displaystyle g_{I}=g_{K}}$である。

以上により、${\displaystyle g_{Y}=g_{I}=g_{K}}$であり、生産の成長率と資本の成長率が一致することが示された。一致する成長率を ${\displaystyle g}$ と表す。

生産の成長率と資本の成長率が一致することをふまえ、技術進歩が労働拡張型になることを以下のとおり示す。

0時点では次の式1であり、また${\displaystyle Y_{t}=Y_{0}e^{gt}}$、${\displaystyle K_{t}=K_{0}e^{gt}}$、${\displaystyle L_{t}=L_{0}e^{g_{L}t}}$であるから、式1は式2のように書ける。関数の1次同次性から式2は式3になる。${\displaystyle A_{t}\equiv e^{(g-g_{L})t}}$と定義すると、式4を得る。

1. ${\displaystyle Y_{0}=F(K_{0},L_{0};0)}$
2. ${\displaystyle Y_{t}e^{-gt}=F(K_{t}e^{-gt},L_{t}e^{-g_{L}t};0)}$
3. ${\displaystyle Y_{t}=F(K_{t},L_{t}e^{(g-g_{L})t};0)}$
4. ${\displaystyle Y_{t}=F(K_{t},A_{t}L_{t};0)}$

関数形の変化を示す最終項がゼロで固定されることは関数形が変化しないことを意味する。最後の式4の関数のなかで ${\displaystyle A_{t}}$ は一定の率で成長し、労働 ${\displaystyle L_{t}}$ を拡張するかのような形になっているので、これを労働拡張型技術進歩という。また ${\displaystyle A_{t}L_{t}}$ を有効労働という。有効労働 ${\displaystyle A_{t}L_{t}}$ は、生産 ${\displaystyle Y_{t}}$ や資本 ${\displaystyle K_{t}}$ と同じ率 ${\displaystyle g}$ で成長する。

黄金律の定理

資本の収益率（利子率）が成長率に等しくなる均斉成長が存在する場合、その均斉成長が黄金律である^[4]。このことをロビンソンは新古典派定理とよんだ^[67]。フェルプスは、黄金時代における消費最大化に関する定理とよんだ^[68]。後にフェルプスはこれを黄金律の定理とよんでいる^[69]。

この定理をPhelps（1965）にもとづいて数式をつかって示すと次のとおりである。

経済構造は次の3つの式であらわされるものとする。

1. ${\displaystyle Y_{t}=F(K_{t},A_{t}L_{t})}$　…時点 ${\displaystyle t}$ の生産物 ${\displaystyle Y_{t}}$ は生産関数 ${\displaystyle F}$ をつうじて資本 ${\displaystyle K_{t}}$ と有効労働 ${\displaystyle A_{t}L_{t}}$ によってつくられる。生産関数 ${\displaystyle F}$ は１次同次関数とする（規模に関して収穫一定）。有効労働 ${\displaystyle A_{t}L_{t}}$ は、技術 ${\displaystyle A_{t}}$ と労働 ${\displaystyle L_{t}}$ を掛け合わせたものであり、まとめて定率 ${\displaystyle {g}}$ で外生的に増加するものとする（労働拡張型技術進歩、前述）。
2. ${\displaystyle Y_{t}=C_{t}+I_{t}}$　…生産物 ${\displaystyle Y_{t}}$ は消費 ${\displaystyle C_{t}}$ にあてられるか投資 ${\displaystyle I_{t}}$ にあてられる。
3. ${\displaystyle {\dot {K_{t}}}=I_{t}-\delta K_{t}}$　…資本 ${\displaystyle K_{t}}$ は投資 ${\displaystyle I_{t}}$ によって増えるが、一定の減耗率 ${\displaystyle \delta }$ で減る。

以上３つの経済構造式を資本の微分方程式のかたちにまとめると次式を得る。

• ${\displaystyle {\dot {K_{t}}}=F(K_{t},A_{t}L_{t})-{\delta }K_{t}-C_{t}}$

外生変数である有効労働 ${\displaystyle A_{t}L_{t}}$ で資本 ${\displaystyle K_{t}}$ と消費 ${\displaystyle C_{t}}$ を割って基準化し、それぞれを小文字 ${\displaystyle k_{t}}$ と ${\displaystyle c_{t}}$ であらわす。規模に関する収穫一定の仮定の下で ${\displaystyle f(k)\equiv F(k,1)}$ と定義すると、上記の微分方程式から ${\displaystyle A_{t}L_{t}}$ を消去できる。

• ${\displaystyle {\dot {k_{t}}}+gk_{t}=f(k_{t})-{\delta }k_{t}-c_{t}}$

均斉成長で資本 ${\displaystyle K_{t}}$ と消費 ${\displaystyle C_{t}}$ は有効労働 ${\displaystyle A_{t}L_{t}}$ と同率で成長するので、有効労働 ${\displaystyle A_{t}L_{t}}$ で基準化された資本水準 ${\displaystyle k_{t}}$ と消費水準 ${\displaystyle c_{t}}$ は均斉成長で一定になる。一定になる資本水準を ${\displaystyle {k}}$ 、消費水準を ${\displaystyle {c}}$ と表すと、上記の式で次のようになる。

• ${\displaystyle c=f(k)-(\delta +g)k}$

そして消費水準 ${\displaystyle c}$ を最大化する黄金律資本 ${\displaystyle k^{*}}$ をもとめる。まず、均斉成長で消費がプラスになるの領域がないとプラスの黄金律は存在しないので、消費がプラスになる領域があることにしよう。生産関数が2回微分可能であり、その1回微分が正で2回微分が負である場合 ${\displaystyle (f'>0,f''<0)}$ 、消費水準 ${\displaystyle c}$ を最大化する黄金律資本 ${\displaystyle k^{*}}$ は、上記の式で ${\displaystyle c}$ を ${\displaystyle k}$ で微分してゼロとなる点である。

• ${\displaystyle f'(k^{*})-\delta -g=0}$

${\displaystyle f'(k)-\delta }$ は資本の純収益率であり、これを利子率 ${\displaystyle r}$ と表す。黄金律利子率 ${\displaystyle r^{*}{\equiv }f'(k^{*})-\delta }$ を用いて次式を得る。

• ${\displaystyle r^{*}=g}$

これにより利子率が成長率に等しい均斉成長が存在し、それが黄金律になることが示された。

微分不能な点のあるハロッド・ドーマー型生産関数の場合も、黄金律を示すことができる。Golden Rule savings rate

新古典派成長モデル

もともとデイヴィッド・キャスやチャリング・クープマンスのモデルは社会計画のための最適成長モデルであったが、後にこれを市場経済における家計の最適化問題におきかえて動学一般均衡モデルとして用いるようになった^[43]。この種の動学一般均衡モデルを新古典派成長モデルなどという^[44]。

新古典派成長モデルでは、均斉成長で利子率が成長率を上まわり、消費が黄金律より少なくなる^[46]。黄金律に達するほど時間選好率を低く設定すると、家計効用が無限大に発散するからである^[50]。このことを以下に示す。

まず企業を考える。企業について次のように想定する^[70]。

• 企業は多数存在し、どれも同じ構造をもつ。
• 企業は競争市場で労働者 ${\displaystyle N_{t}}$ を雇い資本 ${\displaystyle K_{t}}$ を借り生産物 ${\displaystyle Y_{t}}$ を売る。
• 生産技術 ${\displaystyle A_{t}}$ は伸び率 ${\displaystyle a}$ で外生的に上昇する。
• 企業は生産関数 ${\displaystyle Y_{t}=F(K_{t},A_{t}N_{t})}$ で生産を行う。
• 企業は利潤を最大化し、生じた利潤を全て家計に配当する。

生産関数について次のように仮定する。

• ${\displaystyle F}$ は１次同次関数とする（規模に関する収穫一定）^[71]。
• ${\displaystyle f(k)\equiv F(k,1)}$は2回微分可能で${\displaystyle f'(k)>0,f''(k)<0}$とする^[71]。
• ${\displaystyle \lim _{k\to 0}f'(k)=\infty ,\lim _{k\to \infty }f'(k)=0}$とする（稲田の条件）^[72]。

有効労働${\displaystyle A_{t}N_{t}}$あたりの資本を ${\displaystyle k_{t}\equiv K_{t}/A_{t}N_{t}}$ と定義すると、資本の限界生産力は${\displaystyle f'(k_{t})}$と表される^[73]。競争市場であるから資本レンタル料は資本の限界生産力と一致し、また、市場利子率 ${\displaystyle r_{t}}$ は資本レンタル料から資本減耗率 ${\displaystyle \delta }$ を控除した分に等しくなる^[74]。

• ${\displaystyle r_{t}=f'(k_{t})-\delta }$

有効労働の限界生産物は${\displaystyle f(k_{t})-f^{\prime }(k_{t})k_{t}}$で表され、競争市場のもとでそれは有効労働あたりの実質賃金 ${\displaystyle w_{t}}$ と等しくなる^[75]。

• ${\displaystyle w_{t}=f(k_{t})-f^{\prime }(k_{t})k_{t}}$

次に家計を考える。家計について次のように想定する^[70]。

• 家計は多数存在し、どれも同じ構造をもつ。
• 各家計の構成人数は伸び率 ${\displaystyle n}$ で増える。
• 各人は各時点で労働を１単位供給する。
• 家計は資本を保有し企業に貸す。初期時点でどの家計も同じだけ資本を保有する。
• 家計は生涯の効用を最大化するように、所得を消費と貯蓄に分配する

家計の生涯効用は次のように定義される^[76]。

• ${\displaystyle U=\int _{0}^{\infty }e^{-\rho t}u({\frac {C_{t}}{N_{t}}}){\frac {N_{t}}{H}}dt}$

${\displaystyle C_{t}}$は消費の総量、${\displaystyle N_{t}}$は総人口、${\displaystyle H}$は家計の総数であり、したがって${\displaystyle C_{t}/N_{t}}$は一人あたり消費、${\displaystyle N_{t}/H}$は各家計の構成人数である^[70]。関数 ${\displaystyle u}$ は各人の各時点の効用を示し、それにその時点の家計構成人数を乗じた${\displaystyle u(C_{t}/N_{t})N_{t}/H}$は各家計の各時点の効用を表わす^[70]。${\displaystyle \rho }$ は主観的な割引率であり、${\displaystyle \rho }$ が高いほど家計は目先を重視し先行きを軽視する^[70]。

関数 ${\displaystyle u}$ は次のような形を仮定する^[73]。

• ${\displaystyle u(c)={\begin{cases}{\dfrac {c^{1-\theta }}{1-\theta }}&\theta \neq 1,\theta >0\\\log(c)&\theta =1\end{cases}}}$

有効労働あたりの消費${\displaystyle c_{t}\equiv C_{t}/A_{t}N_{t}}$と有効労働の成長率 ${\displaystyle g\equiv a+n}$ を用いて家計の生涯効用を表すと次のとおりである^[77]。

• ${\displaystyle U={\frac {A_{0}^{1-\theta }L_{0}}{H}}\int _{0}^{\infty }e^{-(\rho +\theta a-g)t}u(c_{t})dt}$

また次のように仮定する^[73]。

• 技術進歩を伴う割引の仮定^[78]：${\displaystyle \rho >(1-\theta )a+n}$

この条件を追加することで家計効用が無限大に発散しないことが保証される^[73]。この条件が満たされないと、家計効用が無限大になり家計の最大化問題が適切に設定されない^[73]。この仮定は本節の目的のために重要であり、後で再び登場する。

代表的な家計は、 ${\displaystyle r_{t}}$ や ${\displaystyle w_{t}}$ を所与と考える^[75]。家計の予算制約は、生涯にわたる消費の現在価値が、生涯にわたる労働所得の現在価値と、ゼロ時点の財産の和を超えないことである^[75]。割引因子を

• ${\displaystyle \delta _{t}\equiv e^{-\int _{0}^{t}r_{s}ds}}$

と定義すると、各家計の消費は ${\displaystyle C_{t}/H}$ であり、労働所得は${\displaystyle w_{t}A_{t}N_{t}/H}$であるので、家計の予算制約は次式のとおり表わされる^[79]。

• ${\displaystyle \int _{0}^{\infty }\delta _{t}{\frac {C_{t}}{H}}dt\leq {\frac {K_{0}}{H}}+\int _{0}^{\infty }\delta _{t}w_{t}{\frac {A_{t}N_{t}}{H}}dt}$

これを有効労働あたりで表すと次のとおりである^[80]。

• ${\displaystyle \int _{0}^{\infty }\delta _{t}e^{gt}c_{t}dt\leq k_{0}+\int _{0}^{\infty }\delta _{t}e^{gt}w_{t}dt}$

以上をまとめて家計の最適化問題を設定するためラグランジュ関数を次のように定義する^[81]。

• ${\displaystyle L=\int _{0}^{\infty }e^{-(\rho +\theta a-g)t}u(c_{t})dt}$ ${\displaystyle +\lambda {\bigg [}k_{0}+\int _{0}^{\infty }\delta _{t}e^{gt}w_{t}dt-\int _{0}^{\infty }\delta _{t}e^{gt}c_{t}dt{\bigg ]}}$

各 ${\displaystyle t}$ 時点の ${\displaystyle c_{t}}$ についての1階の条件は次のとおり^[82]（効用関数 ${\displaystyle u}$ の定義をつかう）。

• ${\displaystyle e^{-(\rho +\theta a-g)t}c_{t}^{-\theta }=\lambda \delta _{t}e^{gt}}$

この式の対数をとって時間微分して整理すると次のオイラー方程式を得る^[83]（割引因子 ${\displaystyle \delta _{t}}$ の定義をつかう）。

• ${\displaystyle {\dot {c_{t}}}/{c_{t}}=(r_{t}-\rho -\theta a)\theta ^{-1}}$

また、資本蓄積は次式で与えられる^[84]。

• ${\displaystyle {\dot {k_{t}}}=f(k_{t})-(g+{\delta })k_{t}-c_{t}}$

以上をまとめると次の3つの式によりこの経済モデルは記述されることになる。

1. ${\displaystyle {\dot {c_{t}}}=(r_{t}-\rho -\theta a)\theta ^{-1}c_{t}}$　　（オイラー方程式）
2. ${\displaystyle r_{t}=f'(k_{t})-\delta }$　　（均衡実質利子率）
3. ${\displaystyle {\dot {k_{t}}}=f(k_{t})-(g+{\delta })k_{t}-c_{t}}$　　（資本蓄積式）

均斉成長における値を添え字なしで表わす。均斉成長では次が成り立つ^[85]。

1. ${\displaystyle r=\rho +\theta a}$
2. ${\displaystyle k=f'^{-1}(r+\delta )}$
3. ${\displaystyle c=f(k)-(g+{\delta })k}$

また、均斉成長では成長率が有効労働の成長率${\displaystyle g=a+n}$で決定される^[85]。そして、先に仮定した「技術進歩を伴う割引の仮定」の不等式${\displaystyle \rho >(1-\theta )a+n}$に、${\displaystyle g=a+n}$と上記の式1${\displaystyle r=\rho +\theta a}$を代入すると ${\displaystyle r>g}$ を得る。すなわち均斉成長で利子率が成長率を上まわる。このことは、${\displaystyle \rho >(1-\theta )a+n}$の仮定によって保証される^[85]。先に述べたように、この仮定が満たされないと家計効用が無限大に発散し家計の最適化問題を適切に設定できなくなる^[73]。

${\displaystyle r>g}$ は新古典派成長モデルの均斉成長が黄金律 ${\displaystyle r=g}$ の水準に達しないことを意味する。このように新古典派成長モデルが黄金律に達しないことを修正黄金律という^[86]。また上記の式1 ${\displaystyle r=\rho +\theta a}$ を修正黄金律ということがある^[87]。これを変形黄金則と訳すこともある^[88]。

なお、1989年にオリヴィエ・ブランシャールとスタンレー・フィッシャーによって出版された『マクロ経済学講義』では修正黄金律の定義が少し異なっている^[89]。ブランシャールらは最適化問題の目的関数の定義で人口を乗じず、また技術進歩を考えない。すると、上記の式1は${\displaystyle r=\rho +n}$という形になる。ブランシャールらはこの数式、すなわち均斉成長で利子率が時間選好率と人口増加率の和で決定されるという数式を修正黄金律と呼んでいる^[89]。

脚注

[脚注の使い方]

1. Phelps (1965)またはPhelps (1966)。経済成長の黄金律という表現はPhelps (1966)のタイトル"Golden Rules of Economic Growth"による。
2. ピケティ (2014) 山形浩生らの訳。
3. ^ Phelps (1961)。
4. ^ Phelps (1965)。
5. Phelps (1965)。ここでは大雑把な言い回しをした。くわしくは黄金律の節や黄金律の定理の節を参照。
6. ^ Phelps (1961)の"the Golden Rule of Accumulation"。
7. ^ たとえばBarro and Sala-i-Martin (2004)35頁の"the golden rule of capital accumulation"。
8. ピケティ (2014)593-594頁。
9. ^ Gill and Raiser (2012)Vol.1 Overview 2頁。同Vol.2 Main Report 2頁にも同じ文。
10. ^ Gill and Raiser (2012)Vol.2 Main Report 433頁。
11. Phelps (1961)の"a golden age"。
12. Phelps (2008)はロビンソン夫人が黄金時代を命名したと述べている。Phelps (1961)は参考文献を3つ挙げており、そのうち１つが Robinson (1956)である。Robinson (1956)が黄金時代を定義した件についてはGibson (2005)20頁を参照。
13. Robinson (1956)99頁。Gibson (2005)106頁も参照。
14. ヘシオドス『仕事と日々』。
15. Phelps (1961)などのほか、世代重複モデルの古典として知られるDiamond (1965)なども黄金時代という用語をつかっていた。
16. Barro and Sala-i-Martin (2004)大住圭介訳。均斉成長の原語は balanced growth 。これは均整成長（たとえば朝元照雄「均整成長理論と不均整成長理論』エコノミクス、九州産業大学、2006年）とも均衡成長（たとえばジョーンズ『経済成長理論入門』香西泰監訳、日本経済新聞出版社、1998年）とも訳す。
17. Solow (2000)福岡正夫訳。恒常状態の原語はsteady state。これは持続状態（Barro and Sala-i-Martin (2004) 大住圭介訳）とも定常状態（ジョーンズ『経済成長理論入門』香西泰監訳、日本経済新聞出版社1998年）とも訳す。
18. Barro and Sala-i-Martin (2004)34頁の脚注11。
19. Acemoglu (2009)57頁。原典はKaldor (1961)。
20. Kaldor (1961)。「定型化された事実」は他の経済学者からは「カルドアの事実」ともよばれる（Acemoglu (2009)57頁など）。
21. Solow (2000)福岡正夫訳158頁。
22. ^ Uzawa (1961)、Schlicht (2006)。
23. Phelps (1965)。
24. 齊藤誠（2006）『成長信仰の桎梏：消費重視のマクロ経済学』勁草書房。
25. ^ The Royal Swedish Academy of Sciences. “Edmund Phelps’s Contributions to Macroeconomics” (PDF). Advanced information on Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel. Nobelprize.org. Nobel Media AB. 2015年10月15日閲覧。
26. Phelps (1966)。
27. Phelps (1965)によるリストアップ。Phelps (2008)はジャック・デルソーを外している。
28. Boianovsky and Hoover (2014)。
29. たとえばAcemoglu (2009)42頁。
30. 池田信夫. “池田信夫 blog : 資本収益率はどこで安定するのか”. ライブドア・ブログ. 2015年10月29日閲覧。
31. ^ Phelps (2008)。
32. Phelps (1961)642頁。
33. ^ 大住 (2003)86-87頁。
34. Phelps (1961)639頁。
35. Cass (1965)、Koopmans (1965)。
36. Phelps (1966)。技術進歩のないケースはCass (1965)も参照。
37. Acemoglu (2009)70頁。
38. Howitte (2007)ドラフト版20頁。
39. ^ Mankiw (2015)。
40. ピケティ (2014)第16章注42、専門補遺57頁。山形らの訳では「黄金則」「動的非効率」である
41. ピケティ (2014)専門補遺57頁。山形らの訳では「黄金則」「動的非効率」である。
42. Abel, Mankiw, Summers and Zeckhauser (1989)。
43. ^ Solow (2000)福岡正夫訳「第7章 標準モデル再論」による。
44. ^ Acemoglu (2009)Chapter 8, "The Neoclassical Growth Model"。
45. Barro and Sala-i-Martin (2004)の”the Ramsey model”。
46. ^ Blanchard and Fischer (1989)45頁、Solow (2000)福岡正夫訳167頁。Barro and Sala-i-Martin (2004)98頁と101頁、Acemoglu (2009)310頁。
47. Solow (2000)福岡正夫訳167頁。Acemoglu (2009)300頁。
48. Barro and Sala-i-Martin (2004)101頁。
49. ピケティ (2014)専門補遺57頁。
50. ^ Barro and Sala-i-Martin (2004)101頁、Acemoglu (2009)310-311頁。
51. Diamond (1965)。
52. ^ The Economic Sciences Prize Committee of the Royal Swedish Academy of Sciences, "Market with Search Frictions," Scientific Background on the Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 2010.
53. ^ Tirole (1985)。
54. The Economic Sciences Prize Committee of the Royal Swedish Academy of Sciences, "Jean Tirole: Market Power and Regulation," Scientific Background on the Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 2014.
55. ピケティ (2014)592頁。
56. ^ ピケティ (2014)593頁。
57. ^ ピケティ (2014)594頁。
58. ピケティ (2014)595頁。
59. たとえばピケティ (2014)373～376頁「時間選好の問題」、同592～595頁「21世紀における政府と資本蓄積」などのほか、同書専門増補全般。
60. ピケティ (2014)602頁。
61. Barro and Sala-i-Martin (2004)35頁。
62. 大住（2003）86頁の注2。
63. Robinson (1938)。
64. Uzawa (1961)。
65. Schlicht (2006)。
66. Schlicht (2006)のほか、Jones and Scrimgeour (2008)、Acemoglu (2009)を参照。
67. Robinson (1962)、A Neo-Classical Theorem。
68. Phelps (1965)の a theorem on maximal consumption in a golden age 。
69. Phelps (2008)。
70. ^ ローマー (1998)46頁。
71. ^ Acemoglu (2009)28頁、Assumption 1 参照。
72. Acemoglu (2009)33頁、Assumption 2 参照。
73. ^ ローマー (1998)47頁。
74. Acemoglu (2009)296頁、式8.27参照。
75. ^ ローマー (1998)48頁。
76. ローマー (1998)46頁、式2.1参照。
77. ローマー (1998)50頁、式2.14参照。
78. 仮定の名称は、Acemoglu (2009)310頁、Assumption 4 に由来する。
79. ローマー (1998)48頁、式2.5参照。
80. ローマー (1998)49頁、式2.7参照。
81. ローマー (1998)50頁、式2.15参照。
82. ローマー (1998)51頁、式2.16参照。
83. ローマー (1998)51頁、式2.19参照。
84. Acemoglu (2009)310頁、式8.51参照。
85. ^ Acemoglu (2009)310頁。
86. Solow (2000)福岡正夫訳167頁。Acemoglu (2009)300頁。
87. Barro and Sala-i-Martin (2004)101頁。
88. ピケティ (2014)専門補遺57頁。
89. ^ Blanchard and Fischer (1989)45頁。

参考文献

• Abel, Andrew B.; N. Gregory Mankiw; Lawrence H. Summers; Richard J. Zeckhauser (1989). “Assessing Dynamic Efficiency: Theory and Evidence”. The Review of Economic Studies 56 (1): 1-19. JSTOR 2297746. http://isites.harvard.edu/fs/docs/icb.topic500592.files/abel%20mankiw%20summers%20zeckhauser.pdf. 
• Acemoglu, Daron (2009). Introduction to Modern Economic Growth. Princeton University Press. http://press.princeton.edu/titles/8764.html 
• Barro, Robert J.; Xavier I. Sala-i-Martin (2004). Economic Growth (2nd ed.). The MIT Press 
  • （日本語訳）大住圭介 訳『内生的経済成長理論』（第2版）九州大学出版会、2006年。 
• Blanchard, Olivier J.; Stanley Fischer (1989). Lectures on Macroeconomics. The MIT Press 
  • （日本語訳）高田聖治 訳『マクロ経済学講義』多賀出版、1998年。 
• Mauro, Boianovsky; Kevin D. Hoover (2014). “In the Kingdom of Solovia: The Rise of Growth Economics at MIT, 1956-70”. History of Political Economy (Duke University Press) 46 (1): 198-228. doi:10.1215/00182702-2716172. http://public.econ.duke.edu/~kdh9/Source%20Materials/Research/Boianovsky%20and%20Hoover%20Kingdom%20of%20Solovia.pdf. 
• Cass, David (1965). “Optimum Growth in an Aggregative Model of Capital Accumulation”. The Review of Economic Studies 32 (3): 233–240. JSTOR 2295827. 
• Diamond, Peter (1965). “National Debt in a Neoclassical Growth Model”. The American Economic Review 55 (5): 1126-1150. JSTOR 1809231. https://www.aeaweb.org/aer/top20/55.5.1126-1150.pdf. 
• ローマー, デビッド 著、堀雅博・岩成博夫・南條隆 訳『上級マクロ経済学』（初版）日本評論社、1998年。ISBN 9784535551046。 
• Elgar, Edward, ed (2005). Joan Robinson’s Economics. Edward Elgar Publishing. http://www.uvm.edu/~wgibson/book.pdf 
• Howitt, Peter (2007). “Edmund Phelps: Macroeconomist and Social Scientist”. Scandinavian Journal of Economics 109 (2): 203-224. doi:10.1111/j.1467-9442.2007.00489.x. 
  • （ドラフト版）Howitt, Peter. “Edmund Phelps: Macroeconomist and Social Scientist” (PDF). 2015年11月13日閲覧。　
• Gill, Indermit S.; Martin Raiser (2012). Golden growth : restoring the lustre of the European economic model. The World Bank 
  • “Vol.1 Overview” (PDF). 2015年10月14日閲覧。
  • “Vol.2 Main Report” (PDF). 2015年10月14日閲覧。
  • “Vol.3 Country benchmarks” (PDF). 2015年10月14日閲覧。
• Jones, Charles; Dean Scrimgeour (2008). “A New Proof of Uzawa's Steady-State Growth Theorem”. The Review of Economics and Statistics 90 (1): 180-182. JSTOR 40043136. 
• Kaldor, Nicholas (1961). “Capital Accumulation and Economic Growth”. In F. A. Lutz and Douglas Hague. The Theory of Capital. London: Macmillan. http://laprimaradice.myblog.it/media/00/02/2721930754.pdf 
• Koopmans, Tjalling C. (1965). “On the Concept of Optimal Economic Growth”. The Economic Approach to Development Planning. Chicago: Rand McNally. pp. 225–287 　
• Mankiw, N Gregory (2015). “Yes, r > g. So What?”. The American Economic Review (American Economic Association) 105 (5): 43-47. doi:10.1257/aer.p20151059. 
  • （ドラフト版）Mankiw, N Gregory (November 24, 2014). “Yes, r > g. So What?” (PDF). 2015年11月7日閲覧。　
• 大住圭介『経済成長分析の方法』九州大学出版会〈経済工学シリーズ第2期〉、2003年。 　
• Phelps, Edmund (1961). “The golden rule of accumulation: a fable for growthmen”. The American Economic Review (American Economic Association) 51 (4): 638-643. JSTOR 1812790. http://piketty.pse.ens.fr/files/Phelps1961.pdf. 　
• Phelps, Edmund (1965). “Second Essay on the Golden Rule of Accumulation”. The American Economic Review (American Economic Association) 55 (4): 793-814. JSTOR 1823937. http://piketty.pse.ens.fr/files/PhelpsAER1965.pdf. 
• Phelps, Edmund (1966). Golden Rules of Economic Growth. New York: W.W. Norton 
• Phelps, Edumnd (2008). “golden rule”. In Steven N. Durlauf and Lawrence E. Blume. The new Palgrave dictionary of economics. 3 (2nd ed.). Palgrave Macmillan. pp. 702-703. ISBN 9780333786765 
• ピケティ, トマ 著、山形浩生・守岡桜・森本正史 訳『21世紀の資本』みすず書房、2014年。ISBN 978-4-622-07876-0。 
  • （原書） Thomas Piketty (2013). Le capital au xxie siècle. Editions du Seuil 
  • （オンライン補遺） “トマ・ピケティ『21 世紀の資本』 (みすず書房, 2014.12) 専門補遺” (PDF). 2015年10月19日閲覧。
• Robinson, Joan (1938). “The Classification of Inventions”. The Review of Economic Studies 5 (2): 139–142. JSTOR 2967528. 
• Robinson, Joan (1956). The Accumulation of Capital. London: Macmillan & Co. Ltd 
• Robinson, Joan (1962). “A Neo-Classical Theorem”. The Review of Economic Studies 29 (3): 219-226. JSTOR 2295956. 
• Solow, Robert M. (2000). Growth Theory: An Exposition (second ed.). Oxford University Press 
  • （日本語訳） 福岡正夫 訳『成長理論』（第2版）岩波書店、2000年。 
• Schlicht, Ekkehart (2006). “A Variant of Uzawa’s Theorem”. Economics Bulletin (AccessEcon) 5 (6): 1–5. http://www.economicsbulletin.com/2006/volume5/EB−06E10001A.pdf. 
• Tirole, Jean (1985). “Asset Bubbles and Overlapping Generations”. Econometrica (Econometric Society) 53 (6): 1499-1528. JSTOR 1913232. http://www.math.harvard.edu/archive/21a_fall_14/exhibits/tirole/tirole_assetts.pdf. 
• Uzawa, Hirofumi (1961). “Neutral Inventions and the Stability of Growth Equilibrium”. The Review of Economic Studies 28 (2): 117-124. JSTOR 2295709. 

関連項目

• 経済成長
• 経済成長理論
• 資本蓄積
• 黄金律