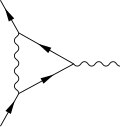
頂点関数

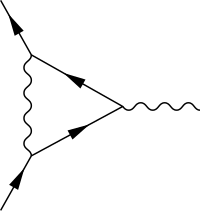
量子電磁力学における3点頂点関数の1ループ補正を表すファインマン・ダイアグラム。波線は光子、実線は電子を表す。

場の量子論において、頂点関数（ちょうてんかんすう、vertex function）とは、複数の粒子が相互作用する過程を記述する相関関数である。量子電磁力学においては、電子のような荷電粒子が仮想的な光子を吸収する（放出する）過程であり、3点頂点関数に対する1ループの頂点補正（ちょうてんほせい、vertex correction）は電子の異常磁気モーメントに支配的な寄与を及ぼす。

概要

頂点関数Γ^μは有効作用Γ_effの汎関数微分によって定義される。量子電磁力学における3点頂点関数は、電磁場との結合定数 eを用いて

${\displaystyle \Gamma ^{\mu }(x,y,z)=-{1 \over e}{\frac {\delta ^{3}\Gamma _{\mathrm {eff} }({\bar {\psi }},\psi ,A_{\mu })}{\delta {\bar {\psi }}(x)\delta \psi (y)\delta A_{\mu }(z)}}}$

となる。

頂点関数Γ^μの中で最も支配的な寄与は、頂点因子に含まれるガンマ行列γ^μである。さらに、頂点関数には量子電磁力学が持つ対称性（ローレンツ対称性、ゲージ対称性）が要請され、その形式はワード＝高橋恒等式によって以下のように制限されている。

${\displaystyle \Gamma ^{\mu }=\gamma ^{\mu }F_{1}(q^{2})+{\frac {i\sigma ^{\mu \nu }q_{\nu }}{2m}}F_{2}(q^{2})}$

ここで、${\displaystyle \sigma ^{\mu \nu }=(i/2)[\gamma ^{\mu },\gamma ^{\nu }]\,}$ であり、q_νは外部から入射する光子の四元運動量である。係数F₁(q²)とF₂(q²)は形状因子(form factor)と呼ばれ、光子の運動量の2乗q²のみに依存する。ダイアグラムの最低次においては、F₁(q²) = 1、F₂(q²) = 0となり、このとき電子は内部構造を持たない点状粒子となっている。それ以上高次のF₁(0)に対する補正は、繰り込みを用いて計算される。形状因子F₂(0)は、電子の異常磁気モーメントaに対応しており、ランデのg因子を用いて以下のように表される。

${\displaystyle a={\frac {g-2}{2}}=F_{2}(0)}$

計算例

量子電磁力学(QED)における3点頂点関数のファインマン・ダイアグラムの計算例を以下に示す。

各々の因子はファインマンルールの定義によって異なるが、ここではフェルミ粒子の伝播関数 ${\displaystyle i/(p\!\!/-m+i\epsilon )}$ 、QEDの頂点因子${\displaystyle -ie\gamma ^{\mu }\,}$などを用いて、1ループの頂点補正を計算する。頂点関数Γ^μは裸の頂点因子γ^μに補正項δΓ^μを加えた形式で表される（頂点因子の係数-ieをつけて表せば、${\displaystyle -ie\Gamma ^{\mu }=-ie\gamma ^{\mu }-ie\delta \Gamma ^{\mu }\,}$）から、δΓ^μに対応するダイグラムを計算すればよい。入射するフェルミ粒子の運動量をp、外部から入射する光子の運動量をq、ループを作る仮想光子の運動量をkとすると、δΓ^μは

= ${\displaystyle \int {\frac {d^{4}k}{(2\pi )^{4}}}(-ie\gamma ^{\nu }){\frac {i}{p\!\!/-k\!\!\!/-m+i\epsilon }}(\gamma ^{\mu }){\frac {i}{k\!\!\!/+q\!\!\!/-m+i\epsilon }}(-ie\gamma ^{\rho }){\frac {-ig_{\nu \rho }}{k^{2}+i\epsilon }}\,}$

となる。上記のダイアグラムには便宜上、フェルミ粒子や光子の外線が引かれているが、頂点補正の計算に含まれるのは実線（フェルミ粒子）2本＋波線（光子）から成るループ部分のみである。

参考文献

• M.E. Peskin; D.V. Schroeder (1995). An Introduction To Quantum Field Theory. Westview Press. ISBN 978-0201503975 

関連項目

• 繰り込み
• 真空偏極
• 自己エネルギー