비음수 행렬 분해

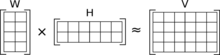
비음수 행렬 분해(Non-negative matrix factorization, NMF)는 음수를 포함하지 않은 행렬 V를 음수를 포함하지 않은 행렬 W와 H의 곱으로 분해하는 알고리즘이다.^[1] 행렬이 음수를 포함하지 않는 성질은 분해 결과 행렬을 찾기 쉽게 만든다. 일반적으로 행렬 분해는 정확한 해가 없기 때문에 이 알고리즘은 대략적인 해를 구하게 된다. 비음수 행렬 분해는 컴퓨터 시각 처리, 문서 분류, 음파 분석, 계량분석화학, 추천 시스템 등에 쓰인다.

비음수 행렬 분해: 행렬 V가 행렬 W와 행렬 H의 곱으로 근사된다.

역사

계량분석화학에서 자기 모델링 그래프 분해라는 이름으로 오랫동안 행해져 왔다. 이 경우 오른쪽 행렬에 있는 벡터들은 떨어져 있는 값보다는 연속적인 값을 갖게 된다. 또 한 핀란드의 연구자들은 양수 행렬 분해라는 이름으로 1990년대 중에 이 알고리즘을 연구해왔다. 연구자 Lee와 Seung이 이 분해의 성질과 두 개의 간단한 분해 알고리즘을 비음수 행렬 분해로 소개한 뒤 널리 알려졌다.

동기

예를 들어

• 10000x500 크기의 단어들을 포함한 행렬 V가 있다고 하자. V의 500개의 열(벡터)은 문서를 나타낸다.
• 이 행렬 V를 10000x10과 10x500의 크기를 가지는 W와 H로 분해했다고 하자. W는 10개의 열을 가지고 있는 행렬이다.
• V=WH이기 때문에 행렬 V는 W의 선형 결합으로 나타내어지는 행렬이다. 따라서 W의 열 벡터들은 V의 특징 벡터라고 할 수 있다. 즉, V가 포함한 단어들의 특징을 분석한 행렬이 W라는 것이다.

이처럼 커다란 정보를 특징과 계수들로 어림 잡아 분해하여 정보의 특징을 파악하는 데에 쓰인다.

종류

근사적인 비음수 행렬 분해

일반적으로 W의 열 개수와 H의 행 개수가 WH=V가 되도록 결정된다. 기존 행렬 V와 분해한 비음수 행렬 W와 H의 곱과의 차이를 오차 U라고 이야기한다. V=WH+U. U의 원소들은 양수나 음수가 될 수 있다. W와 H의 크기가 V보다 작기 때문에 저장하거나 다루기에 용이하다. 또 V를 원래 정보보다 상대적으로 적은 정보로 표현하여 분해한 행렬 하나가 전체 정보의 대략적인 정보를 제시할 수 있다.

볼록 비음수 행렬 분해

기존 비음수 행렬 분해에서는 W는 어떤 행렬도 될 수 있지만 볼록 비음수 행렬 분해에서는 W를 기존 입력 벡터들${\displaystyle (v_{1},\cdots ,v_{n})}$의 볼록 결합으로 제한하기 때문에 W에 포함된 정보의 질이 크게 향상된다. 또한, 결과 행렬 H가 더 직교화되는 효과가 생긴다.

음수가 아닌 랭크 분해 (Non-negative rank factorization, NRF)

V의 음수가 아닌 랭크가 V의 랭크와 같다면 V=WH를 음수가 아닌 랭크 분해라고 한다. 음수가 아닌 랭크 분해를 찾는 것은 NP-난해이다.

여러 가지 비용 함수와 정형화 기법

어떤 비용 함수를 사용하느냐, 어떤 정형화 기법을 사용하느냐에 따라 분해의 종류가 나뉜다. 널리 쓰이는 두 가지 분해 방법에는 Lee와 Seung가 연구한 최소 제곱 오차와 양수 행렬에 대한 쿨백-라이블러 발산(Kullback–Leibler divergence) 방법을 이용한 것이 있다. 두 방법은 다른 알고리즘으로 취급된다. 가장 보편적인 최소 제곱 오차를 이용한 분해를 아래에 서술한다. 다른 분해의 방법으로는 총 표준 변화를 이용한 방법이 있다. L1 정칙화가 최소 제곱 오차에 같이 사용되었을 때 성긴 코딩과 형태가 유사하여 음수가 아닌 성긴 코딩이라고도 부른다.

온라인 NMF

비음수 행렬 분해는 입력 데이터를 한번에 다루는 특징이 있다. 따라서 이 알고리즘은 저장하기에 너무 크거나 스트리밍과 같은 데이터에 대해서는 적용하기 힘들다. 이렇게 많은 사용자나 많은 입력이 있거나 새로운 정보가 계속 들어와 계산을 새로 해야하는 경우에는 협업 필터링을 사용할 수도 있다. 이 때 비용 함수는 같을 수도 다를 수도 있지만 알고리즘은 달라져야 한다.

알고리즘

비음수 행렬 ${\displaystyle \mathbf {V} }$에 근사하는 행렬곱 ${\displaystyle \mathbf {WH} }$을 찾기 위해 최신화 규칙을 반복해서 시행하면, 비용 함수의 함수값을 수렴 조건이 만족할 때까지 감소시킬 수 있고 이를 통해 구하고자 했던 분해된 행렬 ${\displaystyle \mathbf {W} }$와 ${\displaystyle \mathbf {H} }$를 얻을 수 있다. 이 때 수렴은 항상 보장된다.

즉, 알고리즘을 1) 비용 함수 2) 최신화 규칙 3) 수렴 보장으로 나누어 분석할 수 있다.

비용 함수

비용 함수에는 크게 두가지가 있다. 첫 번째 비용함수는 최소 제곱 오차로 아래 수식과 같이 표현할 수 있으며,
${\displaystyle F(\mathbf {A} ,\mathbf {B} )=\|\mathbf {A} -\mathbf {B} \|^{2}=\sum _{i,j}(A_{ij}-B_{ij})^{2}}$
0을 하한값으로 하며 A=B일 때 하한값을 취하게 된다.

두 번째 비용함수는 B로부터 A의 발산값으로, 아래 수식과 같이 표현할 수 있다.
${\displaystyle D(A||B)=\sum _{i,j}(A_{ij}\log {\frac {A_{ij}}{B_{ij}}}-A_{ij}+B_{ij})}$
이들 비용함수의 함수값을 최소화하는 방식을 통해, ${\displaystyle \mathbf {V} }$에 근사하는 ${\displaystyle \mathbf {WH} }$를 구한다.

최신화 규칙

각각의 비용함수들의 최신화 규칙과 그에 관한 정리는 아래와 같다.

정리 1. 아래 최신화 규칙 하에서, 최소 제곱 오차 ${\displaystyle \|\mathbf {V} -\mathbf {WH} \|^{2}}$는 비증가함수이다.
${\displaystyle H_{au}}$ ← ${\displaystyle H_{au}{\frac {(W^{T}V)_{au}}{(W^{T}WH)_{au}}}}$

${\displaystyle W_{ia}}$ ← ${\displaystyle W_{ia}{\frac {(VH^{T})_{ia}}{(WHH^{T})_{ia}}}}$
이 최신화 규칙을 통해 얻은 최소 제곱 오차가 불변할 때, W와 H는 임계점(stationary point)에 도달하게 된다. 이 명제의 역도 성립한다.

정리 2. 아래 최신화 규칙 하에서, B로부터 A의 발산값 ${\displaystyle D(A||B)}$은 비증가함수이다.
${\displaystyle H_{au}}$ ← ${\displaystyle H_{au}{\frac {\sum _{i}W_{ia}V_{iu}/(WH)_{iu}}{\sum _{k}W_{ka}}}}$

${\displaystyle W_{ia}}$ ← ${\displaystyle W_{ia}{\frac {\sum _{u}H_{au}V_{iu}/(WH)_{iu}}{\sum _{v}H_{av}}}}$
이 최신화 규칙을 통해 얻은 발산값이 불변할 때, W와 H는 임계점(stationary point)에 도달하게 된다. 이 명제의 역도 성립한다.

정리1과 정리2의 증명을 아래 수렴 보장성 부분에서 확인할 수 있다.

수렴 보장성

[정의]
 모든 h에 대해,
 ${\displaystyle G(h,h')\geq F(h),}$ ${\displaystyle G(h,h)=F(h)}$를 만족하는 ${\displaystyle G(h,h')}$를 ${\displaystyle F(h)}$의 보조 함수라고 한다.

[보조 정리1]
 G가 보조 함수일 때, 함수 F는 비증가함수이다. 즉, ${\displaystyle h^{t+1}=argmin_{h}G(h,h^{t})}$

[보조 정리2]
 행렬 ${\displaystyle K(h^{t})}$가 ${\displaystyle K_{ab}(h^{t})=\delta _{ab}{\frac {(W^{T}Wh^{t})_{a}}{(h_{a})^{t}}}}$를 만족하는 대각 행렬일 때,
 ${\displaystyle G(h,h^{t})=F(h^{t})+(h-h^{t})^{T}}$▽${\displaystyle F(h^{t})+{\frac {1}{2}}(h-h^{t})^{T}K(h^{t})(h-h^{t})}$
 을 만족하는 함수 ${\displaystyle G}$는 ${\displaystyle F(h)={\frac {1}{2}}\sum _{i}(v_{i}-\sum _{a}W_{ia}h_{a})^{2}}$ 의 보조함수이다.

[보조 정리3]
 ${\displaystyle G(h,h^{t})=\sum _{i}(v_{i}logv_{i}-v_{i})+\sum _{ia}W_{ia}h_{a}-\sum _{ia}v_{i}{\frac {W_{ia}(h_{a})^{t}}{\sum _{b}W_{ib}(h_{b})^{t}}}(logW_{ia}h_{a}-log{\frac {W_{ia}(h_{a})^{t}}{\sum _{b}W_{ib}(h_{b})^{t}}})}$
 ${\displaystyle F(h)=\sum _{i}v_{i}log({\frac {v_{i}}{\sum _{a}W_{ia}h_{a}}})-v_{i}+\sum _{a}W_{ia}h_{a}}$ 일 때,
 ${\displaystyle G(h,h^{t})}$는 ${\displaystyle F(h)}$의 보조함수이다.

정리1의 증명

보조정리1의 ${\displaystyle G(h,h^{t})}$를 보조정리2의 ${\displaystyle G(h,h^{t})}$로 바꾸면 아래와 같은 최신화 규칙을 얻는다. ${\displaystyle h^{t+1}=h^{t}-K(h^{t})^{-1}}$▽${\displaystyle F(h^{t})}$ 보조정리2의 ${\displaystyle G(h,h^{t})}$ 가 보조함수이므로, 보조정리1에 의해 함수 F는 비증가함수이다. 방정식을 풀면, ${\displaystyle h_{a}^{t+1}=h_{a}^{t}{\frac {(W^{T}v)_{a}}{(W^{T}Wh^{t})_{a}}}}$ 즉, H에 대한 최신화 규칙을 유도한 것이다. 보조정리1과 보조정리2의 W와 H의 위치를 바꿔주면 W에 대한 최신화 규칙 역시 쉽게 유도할 수 있다.

정리2의 증명

보조정리3에서의 함수 ${\displaystyle G(h,h^{t})}$의 최솟값을 구하기 위해 미분값을 0으로 할 때의 h값을 찾는다. ${\displaystyle {\frac {dG(h,h^{t})}{dh_{a}}}=-\sum _{i}v_{i}{\frac {W_{ia}h_{a}^{t}}{\sum _{b}W_{ib}h_{b}^{t}}}{\frac {1}{h_{a}}}+\sum _{i}W_{ia}=0}$ 그러므로 ${\displaystyle h_{a}^{t+1}={\frac {h_{a}^{t}}{\sum _{b}W_{kb}}}\sum _{i}{\frac {v_{i}}{\sum _{b}W_{ib}h_{b}^{t}}}W_{ia}}$ G가 보조 함수이므로, 함수 F는 최신화를 거듭할수록 그 함수값이 감소 내지 일정하게 유지된다. 위의 식을 행렬 형식으로 바꾸면, 발산값에서의 H 최신화 규칙과 동일한 것을 알 수 있다. H와 W의 위치를 바꿔서, 발산값에서의 W의 최신화 규칙 역시 비증가함을 증명할 수 있다.

성질

정확한 비음수 행렬 분해

일반적으로 비음수 행렬 분해는 근사를 통해 이루어지지만, 추가적인 조건이 더해지면 정확한 행렬 분해를 얻을 수 있다.
1) 행렬 V가 자신의 계수와 같은 계수를 가진 단항 부분 행렬을 가지고 있을 때 정확한 비음수 행렬 분해를 구할 수 있다.
2) 행렬 V가 대칭성을 가지고 있으며 자신의 계수와 같은 계수를 가진 대각 부분 행렬을 가지고 있을 때, 정확한 비음수 행렬 분해를 구할 수 있다.
3) 행렬 W가 분리 조건을 만족하면 정확한 비음수 행렬 분해를 구할 수 있다.

유일성 유무 판단

비음수 행렬 분해는 유일성을 가지지 않는다. ${\displaystyle \mathbf {WH} =\mathbf {WBB} ^{-1}\mathbf {H} }$이고, 만약 새로운 행렬 ${\displaystyle \mathbf {{\tilde {W}}=WB} }$ 과 ${\displaystyle \mathbf {\tilde {H}} =\mathbf {B} ^{-1}\mathbf {H} }$ 가 음수항을 가지고 있지 않다면, 또다른 행렬 분해를 구할 수 있다.

군집 성질

비음수 행렬 분해는 군집 성질을 가진다. 즉, 이 행렬 분해는 입력 자료 행렬${\displaystyle \mathbf {V} =(v_{1},\cdots ,v_{n})}$의 행들을 무조건 군집화한다. 구체적으로, ${\displaystyle \mathbf {V} }$를 ${\displaystyle \mathbf {V} \simeq \mathbf {W} \mathbf {H} }$ 로 근사할 때 오차 함수${\displaystyle \min _{W,H}||V-WH||_{F},W\geq 0,H\geq 0}$를 최소화하는 방식을 택한다. 만약 ${\displaystyle HH^{T}=I}$ 라는 조건이 추가된다면, 위의 최소화 과정은 K-평균 군집화의 최소화과정과 동일-음이 아니라는 것만 제외하면-한 것이다. 최소 제곱 오차가 아닌 발산값을 비용 함수로 고려하는 경우에 이 행렬 분해는, 이미 대중적인 문서 군집 방법인 확률적 잠재 의미 분석과 동일하다.

다른 학습기법과의 관계

• Learning the parts of objects by non-negative matrix factorization에서는 비음수 행렬 분해를 이용하여 부분 기반 사진 분해를 하였다. 이 논문에서 비음수 행렬 분해를 벡터 정량화나 주성분 분석 기법과 비교했는데, 세 기법 모두 분해를 기반하고 있지만 제약 조건이 달라 결과가 모두 다르게 나왔다.
• 비음수 행렬 분해는 좀 더 일반적인 확률 모델인 다항 주성분 분석 기법과 동일시 될 수 있다. 특히, Kullback-Leibler 발산값을 최소화시키면, 비음수 행렬 분해는 확률적 잠재 의미 분석과 동일시 될 수 있다.
• 비음수 행렬 분해는 완화된 형태의 k 평균 알고리즘으로 동일시 할 수 있다. 이는 비음수 행렬 분해를 데이터 군집화에 사용하는 이론적 토대가 된다. 그러나 k-평균 알고리즘은 비음수이라는 제약 조건을 가지고 있지 않다는 차이가 있다.
• 비음수 행렬 분해는 2개 층을 가진 베이즈 네트워크 모델로 볼 수도 있다.

응용 사례

텍스트 마이닝

비음수 행렬 분해는 텍스트 마이닝에 응용할 수 있다. 텍스트 마이닝에서 문서-용어 행렬은 문서에서 용어들의 가중치 정보를 담고 있다. 이 행렬은 비음수 행렬 분해를 이용하여 용어-요소 행렬과 요소-문서 행렬로 분해할 수 있다. 이 요소들은 문서의 내용으로부터 도출되고, 요소-문서 행렬은 관련 문서들의 정보 군집에 대한 정보를 담는다.

스펙트럼 데이터 분석

비음수 행렬 분해는 스펙트럼 데이터 분석에 응용할 수 있다. 한 가지 예시로, 비음수 행렬은 우주 상의 물체와 파편을 구분짓는데 쓰였다.

생물 정보 공학

비음수 행렬 분해는 유전자 발현 데이터를 그룹화하고, 군집된 데이터의 대표적인 유전자를 찾는데에 응용할 수 있다.

인터넷 거리 예측

비음수 행렬 분해는 인터넷 상의 거리 예측에 응용할 수 있다. 예를 들어, N개의 호스트가 있다고 하자. 각각의 호스트 사이의 거리 정보는 N×N 행렬 안에 담을 수 있고, 이를 예측해 볼 수 있다.

최근 연구 동향

비음수 행렬 분해에서는 다양하게 연구가 진행되고 있지만, 특히 다음 영역에서의 연구를 포함한다.

알고리즘

요소의 초기화나 요소의 광역 최솟값을 찾는 법에 대한 연구가 진행 중이다.

확장성

엄청나게 큰 크기의 행렬을 분해하는 방법에 대한 연구가 진행 중이다. 웹 데이터 마이닝 분야 같은 곳에서는 굉장히 큰 데이터가 빈번하게 쓰여 지고 있고, 이는 분산 기법을 도입한 분산 비음수 행렬 분해에 대한 연구로 이어지고 있다.

동적 학습

데이터가 들어올 때마다 분해를 업데이트 해줄 수 있는 연구가 진행 중이다.

관련 라이브러리

C

Linux에서 이용할 수 있다. https://web.archive.org/web/20150201024802/http://www.cs.virginia.edu/~jdl/nmf/

Python

파이썬은 자체적으로 nimfa라는 NMF 라이브러리를 가지고 있다. 관련 API: https://web.archive.org/web/20180423194531/http://nimfa.biolab.si/

JAVA

자바에서 기계학습을 위한 라이브러리를 제공하는 곳이다. http://sourceforge.net/projects/jlml/files/JML/

Matlab

매트랩에는 비음수 행렬 분해를 수행하는 함수가 있다. 관련 API: http://kr.mathworks.com/help/stats/nnmf.html

참조 논문 및 자료

각주

1. Tandon, Rashish; Suvrit Sra (2010). “Sparse nonnegative matrix approximation: new formulations and algorithms” (PDF). TR. 

관련논문

• J. Shen, G. W. Israël (1989). “A receptor model using a specific non-negative transformation technique for ambient aerosol”. 《Atmospheric Environment》 23 (10): 2289–2298 (영어). doi:10.1016/0004-6981(89)90190-X. 
• Pentti Paatero (1997). “Least squares formulation of robust non-negative factor analysis”. 《Chemometrics and Intelligent Laboratory Systems》 37 (1): 23–35 (영어). doi:10.1016/S0169-7439(96)00044-5. 
• Raul Kompass (2007). “A Generalized Divergence Measure for Nonnegative Matrix Factorization”. 《Neural Computation》 19 (3): 780–791 (영어). doi:10.1162/neco.2007.19.3.780. PMID 17298233. 
• Liu, W.X. and Zheng, N.N. and You, Q.B. (2006). “Nonnegative Matrix Factorization and its applications in pattern recognition” (PDF). 《Chinese Science Bulletin》 51 (17–18): 7–18 (영어). doi:10.1007/s11434-005-1109-6.  CS1 관리 - 여러 이름 (링크)^{[깨진 링크(과거 내용 찾기)]}
• Ngoc-Diep Ho, Paul Van Dooren and Vincent Blondel (2008). “Descent Methods for Nonnegative Matrix Factorization”. arXiv:(영어) 0801.3199 (영어) |arxiv= 값 확인 필요 (도움말) [cs.NA].  더 이상 지원되지 않는 변수를 사용함 (도움말)
• Andrzej Cichocki, Rafal Zdunek and Shun-ichi Amari (2008). “Nonnegative Matrix and Tensor Factorization”. 《IEEE Signal Processing Magazine》 25 (1): 142–145 (영어). doi:10.1109/MSP.2008.4408452. 
• Cédric Févotte, Nancy Bertin, and Jean-Louis Durrieu (2009). “Nonnegative Matrix Factorization with the Itakura-Saito Divergence: With Application to Music Analysis”. 《Neural Computation》 21 (3): 793–830 (영어). doi:10.1162/neco.2008.04-08-771. PMID 18785855.  CS1 관리 - 여러 이름 (링크)
• Ali Taylan Cemgil (2009). “Bayesian Inference for Nonnegative Matrix Factorisation Models”. 《Computational Intelligence and Neuroscience》 2009 (2): 1 (영어). doi:10.1155/2009/785152. PMC 2688815. PMID 19536273. ^{[깨진 링크(과거 내용 찾기)]}

같이 보기

• 다중선형대수학
• 텐서