아다마르 곱

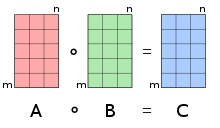
선형대수학에서 아다마르 곱(영어: Hadamard product)은 같은 크기의 두 행렬의 각 성분을 곱하는 연산이다. 즉, 일반 행렬곱은 ${\displaystyle m\times n}$과 ${\displaystyle n\times p}$의 꼴의 두 행렬을 곱하지만, 아다마르 곱은 ${\displaystyle m\times n}$과 ${\displaystyle m\times n}$의 꼴의 두 행렬을 곱한다. 덧셈에 대하여 분배 법칙을 따른다. 기호는 ${\displaystyle \bigcirc }$.

정의

환 ${\displaystyle R}$의 성분을 갖는, 같은 크기 ${\displaystyle m\times n}$의 두 행렬

${\displaystyle M,N\in \operatorname {Mat} (m,n;R)}$

${\displaystyle M={\begin{pmatrix}M_{11}&M_{12}&\dotsm &M_{1n}\\M_{21}&M_{22}&&M_{2n}\\\vdots &&\ddots &\vdots \\M_{m1}&M_{m2}&\dotsm &M_{mn}\end{pmatrix}}}$

${\displaystyle N={\begin{pmatrix}N_{11}&N_{12}&\dotsb &N_{1n}\\N_{21}&N_{22}&&N_{2n}\\\vdots &&\ddots &\vdots \\N_{m1}&N_{m2}&\dotsm &N_{mn}\end{pmatrix}}}$

이 주어졌다고 하자. 그렇다면, ${\displaystyle M}$과 ${\displaystyle N}$의 아다마르 곱은 다음과 같다.

${\displaystyle M\bigcirc N={\begin{pmatrix}M_{11}N_{11}&M_{12}N_{12}&\dotsm &M_{1n}N_{1n}\\M_{21}N_{21}&M_{22}N_{22}&&M_{2n}N_{2n}\\\vdots &&\ddots &\vdots \\M_{m1}N_{m1}&M_{m2}N_{m2}&\dotsm &M_{mn}N_{mn}\end{pmatrix}}\in \operatorname {Mat} (m,n;R)}$

성질

환 ${\displaystyle R}$가 주어졌다고 하자.

아다마르 곱은 결합 법칙과 덧셈에 대한 분배 법칙을 따른다. 즉, 임의의

${\displaystyle M,N,P\in \operatorname {Mat} (m,n;R)}$

에 대하여, 다음이 성립한다.

${\displaystyle (M\bigcirc N)\bigcirc P=M\bigcirc (N\bigcirc P)}$

${\displaystyle M\bigcirc (N+P)=M\bigcirc N+M\bigcirc P}$

${\displaystyle (N+P)\bigcirc M=N\bigcirc M+P\bigcirc M}$

아다마르 곱의 항등원은 모든 성분이 1인 행렬

${\displaystyle {\mathsf {J}}_{m\times n}={\begin{pmatrix}1&1&\dotsm &1\\1&1&&1\\\vdots &&\ddots &\vdots \\1&1&\dotsm &1\end{pmatrix}}}$

이다. 이에 따라, ${\displaystyle (\operatorname {Mat} (m,n;R),\bigcirc ,{\mathsf {J}})}$는 환을 이루며, 이는 환의 직접곱 ${\displaystyle R^{mn}}$과 동형이다.

만약 ${\displaystyle R}$가 가환환이라면, 아다마르 곱은 교환 법칙을 따른다. 즉, 임의의

${\displaystyle M,N\in \operatorname {Mat} (m,n;R)}$

에 대하여, 만약 ${\displaystyle R}$가 가환환일 경우 다음이 성립한다.

${\displaystyle M\bigcirc N=N\bigcirc M}$

만약 ${\displaystyle M\in \operatorname {Mat} (m,n;R)}$의 모든 성분이 가역원이라면, ${\displaystyle M}$에 대한 아다마르 곱은 다음과 같은 역원을 갖는다.

${\displaystyle M^{\bigcirc -1}={\begin{pmatrix}M_{11}^{-1}&M_{12}^{-1}&\dotsm &M_{1n}^{-1}\\M_{21}^{-1}&M_{22}^{-1}&&M_{2n}^{-1}\\\vdots &&\ddots &\vdots \\M_{m1}^{-1}&M_{m2}^{-1}&\dotsm &M_{mn}^{-1}\end{pmatrix}}}$

두 대칭 행렬의 아다마르 곱은 대칭 행렬이다. 두 복소수 에르미트 행렬의 아다마르 곱은 에르미트 행렬이다.

슈어-오펜하임 부등식

임의의 두 양의 준정부호 에르미트 행렬

${\displaystyle M,N\in \operatorname {Mat} (n,n;\mathbb {C} )}$

${\displaystyle M=M^{*}}$

${\displaystyle N=N^{*}}$

${\displaystyle v^{*}Mv\geq 0\forall v\in \mathbb {C} ^{n}}$

${\displaystyle v^{*}Nv\geq 0\forall v\in \mathbb {C} ^{n}}$

이 주어졌다고 하자. 그렇다면, 슈어-오펜하임 부등식(Schur-Oppenheim不等式, 영어: Schur–Oppenheim inequality)에 따르면, 다음이 성립한다.

• ${\displaystyle M\bigcirc N}$은 역시 양의 준정부호 에르미트 행렬이다.
• ${\displaystyle \det(M\bigcirc N)\geq \left(\prod _{i=1}^{n}\prod _{j=1}^{n}M_{ij}\right)\det N\geq \det(MN)}$

역사

“아다마르 곱”이라는 용어는 자크 아다마르의 이름을 딴 것이다.

슈어-오펜하임 부등식의 경우, 이사이 슈어가 1911년에 ${\displaystyle \det(M\bigcirc N)\geq \det(MN)}$을 증명하였으며,^{[1]:14, Satz Ⅶ} 알렉산더 오펜하임(영어: Alexander Oppenheim, 1903~1997)이 1930년에 이를 개량하였다.^[2]

같이 보기

• 크로네커 곱

각주

1. Schur, J. (1911). “Bemerkungen zur Theorie der beschränkten Bilinearformen mit unendlich vielen Veränderlichen”. 《Journal für die reine und angewandte Mathematik》 (독일어) 140: 1–28. doi:10.1515/crll.1911.140.1. ISSN 0075-4102. JFM 42.0367.01. 
2. Oppenheim, Alexander (1930년 4월). “Inequalities connected with definite Hermitian forms”. 《Journal of the London Mathematical Society》 (영어) 5 (2): 114–119. doi:10.1112/jlms/s1-5.2.114. JFM 56.0106.05. 

외부 링크

• “Matrix multiplication”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4. 
• Million, Elizabeth (2007년 4월 12일). “The Hadamard product” (PDF) (영어).