자쿠르-테트로데 방정식

자쿠르-테트로데 방정식 (Sackur-Tetrode equation)은 단원자 이상 기체의 엔트로피를 나타내는 식이다.^[1]

이 식은 휘호 마르틴 테트로데^[2] (1895-1931)와 오토 자쿠르^[3] (1880-1914)의 이름을 따서 명명되었다. 이들은 1912년 거의 동시에 볼츠만의 기체 통계 및 엔트로피 방정식의 해로 이 식을 독립적으로 찾아냈다.^[4]

공식

자쿠르-테트로데 방정식은 단원자 이상기체의 엔트로피 ${\displaystyle S}$를 그 기체의 열역학적 상태에 관한 항, 구체적으로 단원자 이상 기체의 부피 ${\displaystyle V}$, 내부 에너지 ${\displaystyle U}$, 및 입자의 수 ${\displaystyle N}$으로 표현한다.^[1][4]

${\displaystyle {\frac {S}{k_{\rm {B}}N}}=\ln \left[{\frac {V}{N}}\left({\frac {4\pi m}{3h^{2}}}{\frac {U}{N}}\right)^{3/2}\right]+{\frac {5}{2}},}$

여기서 ${\displaystyle k_{\mathrm {B} }}$ 는 볼츠만 상수, ${\displaystyle m}$ 는 기체 입자의 질량이고 ${\displaystyle h}$ 플랑크 상수이다.

이 방정식을 열 파장 ${\displaystyle \Lambda }$를 이용하여 표현하면 아래와 같디 쓸 수 있다.

${\displaystyle {\frac {S}{k_{\rm {B}}N}}=\ln \left({\frac {V}{N\Lambda ^{3}}}\right)+{\frac {5}{2}},}$

고전적 및 양자적 이상 기체( 페르미 기체, 보스 기체 )의 3차원 엔트로피 대 온도 곡선. 고온에서는 모두 서로 일치하지만 고전적 엔트로피(자쿠르-테트로데 방정식)가 음수 값에 접근하기 시작하는 저온에서는 일치하지 않는다.

자쿠르-테트로데 방정식의 유도에 대해서는 기브스 역설 항목을 참조. 열역학만이상 에 의하여 기체의 엔트로피에 적용되는 제한 조건에 대해서는 이상 기체 항목 참조.

위의 식은 기체가 고전적 영역에 있고 ("올바른 볼츠만 계수"를 하는) 맥스웰-볼츠만 통계로 기술 할 수 있다고 가정한다. 열 파장의 정의에 의하면, 이는 자쿠르-테트로데 방정식이 다음 경우에만 유효함을 의미한다.

${\displaystyle {\frac {V}{N\Lambda ^{3}}}\gg 1.}$

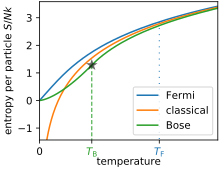
자쿠르-테트로데 방정식에 의해 예측된 엔트로피는 온도가 0에 가까워짐에 따라 음의 무한대에 가까워진다.

자쿠르-테트로데 상수

표준 압력 (구체적으로 100 kPa 또는 101.325 kPa)에서 원자 질량 단위 (m_u =1.660 539 066 60(50) × 10 ^-27 kg )^[5]에 해당하는 질량의 입자로 구성되는 이상기체 1몰에 대하여, 자쿠르-테트로데 상수를 S₀/R 로 표현하면, 이는 온도 T = 1 켈빈에서 계산되는 S/k_BN 값과 같다. 2018 CODATA에 의하면 이 값의 권장 값은 다음과 같다.

S₀/R = −1.15170753706(45) for p ^o = 100 kPa^[6]

S₀/R = −1.16487052358(45) for p ^o = 101.325 kPa.^[7]

정보이론적 해석

엔트로피의 열역학적 관점 외에도 정보 이론의 도구를 사용하여 엔트로피의 정보 관점을 제공할 수 있다. 특히 자크르-테트로데 방정식을 정보론적 용어로 유도하는 것이 가능하다. 전체 엔트로피는 4개의 개별 엔트로피, 즉 4개의 별개의 누락된 정보 소스의 합으로 표시된다. 즉, 위치 불확정성, 운동량 불확정성, 양자 역학적 불확정성 원리, 입자의 구별 불가능성 등이 그것이다.^[8] 이 네 조각을 합하면 자크르-테트로데 방정식은 다음과 같이 주어진다.

${\displaystyle {\begin{aligned}{\frac {S}{k_{\rm {B}}N}}&=[\ln V]+\left[{\frac {3}{2}}\ln \left(2\pi emk_{\rm {B}}T\right)\right]+[-3\ln h]+\left[-{\frac {\ln N!}{N}}\right]\\&\approx \ln \left[{\frac {V}{N}}\left({\frac {2\pi mk_{\rm {B}}T}{h^{2}}}\right)^{\frac {3}{2}}\right]+{\frac {5}{2}}\end{aligned}}}$

이 유도에서는 스털링 근사 ${\displaystyle \ln N!\approx N\ln N-N}$ 을 사용한다. 엄밀히 말하면 로그에 대한 차원 인수의 사용은 옳지 않지만 식을 간략하게 하기 위한 "지름길"로 사용한 것이다. 각 대수의 인수를 불특정 표준 질량, 길이 및 시간으로 표현되는 불특정 표준 값으로 나눈 경우 이러한 표준 값은 최종 결과에서 서로 소거되어 동일한 결론이 도출된다. 개별 엔트로피 항은 절대적인 것이 아니라 선택한 표준에 따라 달라지며 더해지는 상수 값에 따라 다른 표준과는 그 값이 상이할 수 있다.

각주

1. Schroeder, Daniel V. (1999), 《An Introduction to Thermal Physics》, Addison Wesley Longman, ISBN 0-201-38027-7 
2. H. Tetrode (1912) "Die chemische Konstante der Gase und das elementare Wirkungsquantum" (The chemical constant of gases and the elementary quantum of action), Annalen der Physik 38: 434–442. See also: H. Tetrode (1912) "Berichtigung zu meiner Arbeit: "Die chemische Konstante der Gase und das elementare Wirkungsquantum" " (Correction to my work: "The chemical constant of gases and the elementary quantum of action"), Annalen der Physik 39: 255–256.
3. Sackur published his findings in the following series of papers:
   1. O. Sackur (1911) "Die Anwendung der kinetischen Theorie der Gase auf chemische Probleme" (The application of the kinetic theory of gases to chemical problems), Annalen der Physik, 36: 958–980.
   2. O. Sackur, "Die Bedeutung des elementaren Wirkungsquantums für die Gastheorie und die Berechnung der chemischen Konstanten" (The significance of the elementary quantum of action to gas theory and the calculation of the chemical constant), Festschrift W. Nernst zu seinem 25jährigen Doktorjubiläum gewidmet von seinen Schülern (Halle an der Saale, Germany: Wilhelm Knapp, 1912), pages 405–423.
   3. O. Sackur (1913) "Die universelle Bedeutung des sog. elementaren Wirkungsquantums" (The universal significance of the so-called elementary quantum of action), Annalen der Physik 40: 67–86.
4. Grimus, Walter (2013). “100th anniversary of the Sackur–Tetrode equation”. 《Annalen der Physik》 525 (3): A32–A35. Bibcode:2013AnP...525A..32G. doi:10.1002/andp.201300720. ISSN 0003-3804. 
5. “2018 CODATA Value: Sackur–Tetrode constant”. 《The NIST Reference on Constants, Units, and Uncertainty》. NIST. 2019년 5월 20일. 2019년 5월 20일에 확인함. 
6. “2018 CODATA Value: Sackur–Tetrode constant”. 《The NIST Reference on Constants, Units, and Uncertainty》. NIST. 2019년 5월 20일. 2019년 5월 20일에 확인함. 
7. “2018 CODATA Value: Sackur–Tetrode constant”. 《The NIST Reference on Constants, Units, and Uncertainty》. NIST. 2019년 5월 20일. 2019년 5월 20일에 확인함. 
8. Ben-Naim, Arieh (2008), 《A Farewell to Entropy: Statistical Thermodynamics Based on Information》, World Scientific, ISBN 978-981-270-706-2, 2017년 12월 12일에 확인함 .

추가 자료

• Emch, G. G.; Liu, C. (2002), 《Logic of Thermostatistical Physics》, Springer-Verlag, Chapter 3: Kinetic theory of gases .
• Koutsoyiannis, D. (2013), “Physics of uncertainty, the Gibbs paradox and indistinguishable particles”, 《Studies in History and Philosophy of Science Part B》 44 (4): 480–489, Bibcode:2013SHPMP..44..480K, doi:10.1016/j.shpsb.2013.08.007 . (This derives a Sackur–Tetrode equation in a different way, also based on information.)
• Paños, F. J.; Pérez, E. (2015), “Sackur–Tetrode equation in the lab”, 《European Journal of Physics》 36 (5): 055033, Bibcode:2015EJPh...36e5033J, doi:10.1088/0143-0807/36/5/055033, S2CID 124422176 .
• Williams, Richard (2009), “The Sackur–Tetrode Equation: How entropy met quantum mechanics”, 《APS News》 18 (8) .

틀:통계 역학 주제