Darbu sumos

Darbu (Darboux) sumos – dvi sąvokos naudojamos apibrėžiant Rymano integralą. Šiomis sumomis apibrėžiamas ir Darbu integralas, kurio apibrėžimas lengvai išplečiamas iki Rymano-Stieltjeso integralo.^[1] Sąvokas pirmą kartą panaudojo Žanas Gastonas Darbu.

Apatinė Darbu suma

Geometrinė apatinės Darbu sumos interpretacija.

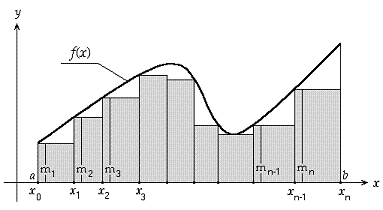
Tegul funkcija ${\displaystyle f(x)}$ apibrėžta intervale ${\displaystyle [a;b]}$. Suskaidome šį intervalą tokiu būdu:

${\displaystyle a=x_{0}<x_{1}<\dots <x_{n-1}<x_{n}=b}$

Gautų intervalų ilgius žymėsime ${\displaystyle \delta x_{i}=x_{i}-x_{i-1}}$ . Jų iš viso yra ${\displaystyle n}$. Ilgiausio gabaliuko ilgį žymėsime ${\displaystyle \Delta }$.

Tokį intervalo skaidinį vadinsime ${\displaystyle T}$. Apibrėžiame tokius taškus:

${\displaystyle m_{i}=\inf _{[x_{i-1};x_{i}]}f(x)}$

T.y. kiekviename intervalo skaidinio gabaliuke surandame mažiausią funkcijos reikšmę. Sudarome tokią sumą:

${\displaystyle s(T)=\sum _{i=1}^{n}m_{i}\Delta x_{i}}$.

Šią sumą ir vadinsime apatine Darbu suma, ji yra intervalo skaidinio ${\displaystyle T}$ funkcija, t. y. ji priklauso nuo to, kokiu būdu skaidome intervalą ${\displaystyle [a;b]}$. Geometrinė apatinės Darbu sumos prasmė yra stačiakampių, besiremiančių į kreivinę trapeciją iš apačios, plotų suma. Šių stačiakampių pločiai priklauso nuo to, kaip skaidome intervalą, t. y. nuo ${\displaystyle T}$.

Viršutinė Darbu suma

Geometrinė viršutinės Darbu sumos interpretacija.

Viršutinę Darbu sumą apibrėžiame labai panašiai. Intervalą ${\displaystyle [a;b]}$ skaidome tokiu pat būtų ir pasirenkame tokius taškus:

${\displaystyle M_{i}=\sup _{[x_{i-1};x_{i}]}f(x)}$

T.y. didžiausias funkcijos reikšmes kiekviename intervalo gabaliuke. Analogiškai sudarome sumą:

${\displaystyle S(T)=\sum _{mn=1}^{n}M_{i}\Delta x_{i}}$.

Ši suma irgi priklauso nuo intervalo skaidymo būdo ${\displaystyle T}$. Geometriškai ji yra kreivinę trapeciją iš viršaus ribojančių stačiakampių plotų suma.

Darbu sumų savybės

Abi Darbu sumos pasižymi tokiomis savybėmis:

• ${\displaystyle S(T_{1})\geq s(T_{2})\;\forall T_{1},T_{2}}$, t. y., kad ir kaip beskaidytume intervalą, viršutinė suma visada bus ne mažesnė už apatinę.
• Pridėjus naujus skaidymo taškus prie esamo skaidinio, apatinė Darbu suma gali tik padidėti, o viršutinė – tik sumažėti.

Šios savybės yra akivaizdžios geometriškai.

Apibrėžiami ir tokie dydžiai:

${\displaystyle {\underline {I}}=\sup _{T}s(T)}$ – didžiausia įmanoma apatinė Darbu suma.

${\displaystyle {\overline {I}}=\inf _{T}S(T)}$ – mažiausia įmanoma viršutinė Darbu suma.

Šie dydžiai pasižymi tokiomis savybėmis:

• ${\displaystyle {\underline {I}}\leq {\overline {I}}}$
• ${\displaystyle \lim _{\Delta \rightarrow 0}s(T)={\underline {I}}}$ ir ${\displaystyle \lim _{\Delta \rightarrow 0}S(T)={\overline {I}}}$, t. y. gabaliukų ilgiams be galo mažėjant, atitinkamos sumos pasiekia savo mažiausią ir didžiausią įmanomas vertes.

Paskutinė savybė dar vadinama Darbu lema.

Šaltiniai

1. Rudin, W. (1976). Principles of Mathematical Analysis (3rd. edition). New York: McGraw-Hill. pp. 120–122. ISBN 007054235X.