Reguliarizavimas (matematika)

Tiek žalias, tiek ir mėlynas sprendinys dera su matavimo taškais. Tačiau priimtinesnis yra glodesnis, žalias sprendinys, paprastai gaunamas parenkant tinkamą reguliarizuojančio nario svorį ${\displaystyle \lambda }$

Reguliarizavimas matematikoje – papildomos (apriorinės) informacijos panaudojimas sprendžiant nekorektiškus uždavinius. Metodiniu požiūriu tai yra Okamo skustuvo principo taikymas atrenkant tinkamus sprendinius iš daugybės kitų.^[1] Žinomiausi reguliarizavimo taikymo pavyzdžiai yra Tichonovo reguliarizavimas ieškant integralinių lygčių sprendinių bei Bajeso metodų taikymas statistikos uždaviniuose.

Tarkime turime integralinę lygtį operatorinėje formoje:

${\displaystyle A\mathbf {x} =\mathbf {b} ,}$

Čia ${\displaystyle A}$ yra operatorius, atvaizduojantis ieškomą vektorių/funkciją ${\displaystyle \mathbf {x} }$ į eksperimentuose gaunamą vektorių/funkciją ${\displaystyle \mathbf {b} }$. Net mažos matavimo paklaidos gali smarkiai paveikti ieškomą ${\displaystyle \mathbf {x} }$. Tuomet vietoj „tikro“, glotnaus, gaunamas smarkiai osciliuojantis sprendinys. Norint to išvengti, šalia mažiausių kvadratų metodu minimizuojamo nario ${\displaystyle \|A\mathbf {x} -\mathbf {b} \|^{2}}$ dar pridedamas papildomas narys ${\displaystyle \|\Gamma \mathbf {x} \|^{2}}$, stabilizuojantis mūsų sprendinį:

${\displaystyle \|A\mathbf {x} -\mathbf {b} \|^{2}+\|\Gamma \mathbf {x} \|^{2}}$

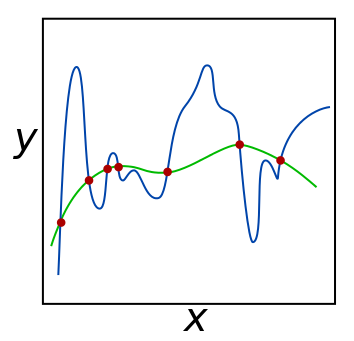
Paprastai papildomas narys būna tiesiog vienetinė matrica: ${\displaystyle \Gamma =\lambda I}$. Tačiau tai gali būti ir operatorius, susijęs su ${\displaystyle \mathbf {x} }$ išvestine. Tinkamai parinkus svorius osciliuojantys sprendiniai atmetami (paveikslėlyje mėlynoji linija) ir paliekami tik glotnūs (žalioji linija).

Šaltiniai

1. Seth, Neha. „What Is Regularization in Machine Learning? Techniques & Methods“. Blogs & Updates on Data Science, Business Analytics, AI Machine Learning. Nuoroda tikrinta 2024-02-03.