Logarytm iterowany

Wykres pokazujący, że iterowany logarytm z 4 (podstawa e) wynosi 2. Krzywa to log(n), a pozostałe linie podążają ścieżką iteracji.

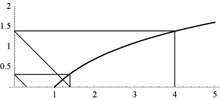
Logarytm iterowany – funkcja używana głównie w teorii złożoności obliczeniowej, dziale informatyki.

Definicja

Logarytm iterowany zdefiniowany jest jako liczba złożeń logarytmu potrzebnych do uzyskania liczby niewiększej od jedności:

${\displaystyle \log ^{*}n:={\begin{cases}0,&{\mbox{dla }}n\leqslant 1;\\1+\log ^{*}(\log n),&{\mbox{dla }}n>1.\end{cases}}}$

Powszechnie definicję uściśla się poprzez użycie logarytmu dwójkowego. Jednak ponieważ w informatyce stosuje się notację dużego O, więc zwykle równie dobrze można zmienić podstawę logarytmu na inną większą od 1. Wynika to z tego, że logarytmy o różnych (większych niż 1) podstawach są wprost proporcjonalne (współczynnik proporcjonalności jest dodatni; jeśli ${\displaystyle a>1}$ i ${\displaystyle b>1,}$ to ${\displaystyle \log _{a}c=\log _{a}b\cdot \log _{b}c,}$ gdzie liczba ${\displaystyle \log _{a}b>0}$).

Logarytm iterowany jest dobrze zdefiniowaną funkcją dla podstaw większych niż

${\displaystyle e^{1/e}\approx 1{,}444667.}$

W przeciwnym razie wyrażenie może nie być zbieżne.

Własności

Jest to funkcja bardzo wolno rosnąca, przykładowo dla wszystkich

${\displaystyle n\leqslant 2^{65536}=2^{2^{2^{2^{2}}}}}$

wartość logarytmu iterowanego nie przekracza 5, a wiadomo, że ${\displaystyle 2^{65536}>10^{19600}.}$ Z tego względu, dla większości zastosowań praktycznych wartość tej funkcji jest niewielka.