Polígono construtível

Um polígono construtível é um polígono regular que pode ser construído com régua e compasso.
Teorema de Gauss–Wantzel
[editar | editar código-fonte]O teorema de Gauss–Wantzel afirma que um polígono regular de lados é construtível com régua e compasso, se, e somente se, pode ser escrito como uma potência de 2 ou como o produto de uma potência de 2 por primos de Fermat distintos.[1] Isto é, se puder ser escrito de uma das duas formas:
- , ,
- ou
- , em que e são os primos de Fermat, ou seja, são números primos da forma , ; tal que , para quaisquer e .
Primeiros polígonos construtíveis
[editar | editar código-fonte]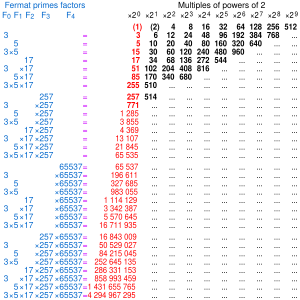
Pelo teorema provado por Gauss e Wantzel, os primeiros polígonos construtíveis resultam ter o seguinte número de lados:
- n = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272, 320, 340, 384, 408, 480, 510, 512, 514, 544, 640, 680, 768, 771, 816, 960, 1020, 1024, 1028, 1088, 1280, 1285, 1360, 1536, 1542, 1632, 1920, 2040, 2048, ... (sequência A003401 na OEIS),
Referências
- ↑ Eliane Quelho Frota Rezende, Maria Lúcia Bontorim de Queiroz - Geometria Euclidiana Plana e Construções Geométricas, Editora Unicamp, 2ª Edição, pág. 168
Ver também
[editar | editar código-fonte]Galeria
[editar | editar código-fonte]
Da esquerda para a direita, construções de 15-gono, 17-gono, 257-gono e 65537-gono. Apenas o primeiro estágio da construção do 65537-gonl é mostrado; as construções do 15-gonl, 17-gonl e 257-gonl são dadas completas.













