Profundidade de bit de áudio

Um sinal analógico (em vermelho) codificado em amostras digitais PCM de 4 bits (em azul); a resolução de profundidade da onda é 4, então cada amplitude da amostra tem 1 de 16 valores possíveis. (4 bits = 2⁴ = 16)

Em áudio digital usando modulação codificada de pulsos (PCM - Pulse Code Modulation), profundidade de bit é o número de bits de informação em cada amostra, que corresponde diretamente à resolução delas. Exemplos de profundidade de bit incluem CDs, que usam 16 bits por amostra, DVD de áudio e Bluray, que podem suportar até 24 bits por amostra.

A profundidade de bit afeta principalmente o nível de ruído de erros da quantização mais a proporção sinal-ruído (signal-to-noise ratio) e além do alcance dinâmico. Entretanto, técnicas como dithering, modelamento de ruído e sobreamostragem (oversampling) suavizam estes efeitos sem mudar a profundidade de bit. Ela também afeta o bit rate e o tamanho do arquivo de áudio.

Para um sinal modulado por código de pulsos (PCM), a profundidade de bit é a única referência significativa. Formatos não-PCM, como os comprimidos com perdas de dados, não têm profundidade de bit associada. Por exemplo, no formato MP3, a quantização é feita usando o domínio da frequência representando o sinal, não com base no domínio do tempo com profundidade de bits relevantes às amostras.

Representação binária

Um sinal PCM é uma sequência de amostras de áudio digital contendo os dados de informação necessários para a reconstrução do sinal analógico original. Cada amostra representa a amplitude do sinal em um ponto específico no tempo, e elas são uniformemente espaçadas nele. A amplitude é a única informação explícita armazenada na amostra, que é normalmente armazenada tanto em números inteiros ou em números com vírgula flutuante, codificada como um número binário com um número fixo de dígitos: a profundidade de bit ou resolução da amostra, que também se refere como tamanho de palavra (word length) ou word size.

A resolução indica o número de valores inteiros que podem representar o alcance (possibilidades) de valores analógicos. A resolução dos inteiros binários aumenta exponencialmente enquanto o tamanho de palavra aumenta. Adicionando um bit se dobra a resolução, adicionando dois, quadruplica, e assim em diante. O número de valores possíveis que podem ser representados por um inteiro, pode ser calculado usando 2ⁿ, onde n é a profundidade de bit. Enfim, um sistema de 16 bits tem uma resolução de 65.536 (2¹⁶) valores possíveis ^[1]. Dados de áudio PCM são normalmente armazenados como números com sinal no formato complemento para dois.

Muitos formatos de arquivos de áudio e estações de trabalho de áudio digital (DAW) suportam formatos PCM com amostras representadas por números com vírgula flutuante ^[2][3][4][5]. Ambos os formatos WAV e o AIFF suportam representações em números com vírgula flutuante ^[6][7]. Diferentemente de números inteiros, um número com vírgula flutuante é composto de campos separados que matematicamente se relacionam para formar um número racional. O padrão mais comum é o IEEE 754 que é composto de três campos: um bit de sinal que representa se o número é positivo ou negativo, um expoente e um significando que é multiplicado pelo expoente. O significando é representado como uma fração binária de números com vírgula flutuante de base de dois pelo IEEE ^[8].

Quantização

Amostragem e quantização de um sinal (vermelho) para 4-bit PCM

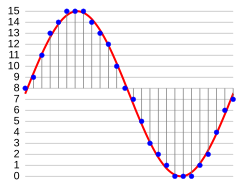
A profundidade de bit limita a relação sinal-ruído do sinal reconstruído a um nível máximo determinado pelo erro de quantização. A profundidade de bit não tem nenhum impacto na resposta em frequência, a qual é restringida pela amostragem de sinal.

O erro de quantização introduzido durante a conversão analógico-digital (A/D) é chamado de ruído de quantização. Não é possível uma representação perfeita de um sinal analógico para digital, pois entre zero e o valor máximo possível, um sinal analógico passa por todos os valores intermediários possíveis (que são infinitos), enquanto o sinal digital só pode assumir um número pré-determinado (finito) de valores^[9]. O ruído de quantização é um erro de arredondamento entre o valor da voltagem de entrada analógico para o conversor e o valor digitalizado de saída. O ruído é não-linear e é dependente do sinal de entrada.

Um número binário de 8 bits (149 em decimal), com o último bit significante destacado

Em um conversor analógico-digital ideal, onde o erro de quantização é uniformemente distribuído entre ${\displaystyle \scriptstyle {\pm {\frac {1}{2}}}}$ do último bit significante (Least Significant Bit - LSB) e onde o sinal tem uma distribuição uniforme cobrindo todos os níveis de quantização, a relação sinal / ruído de quantização pode ser calculada usando:

${\displaystyle \mathrm {RSRQ} =20\log _{10}(2^{Q})\approx 6.02\cdot Q\ \mathrm {dB} \,\!}$

Onde Q é o número de bits da quantização e o resultado é medido em decibéis (dB) ^[10].

Portanto, áudio digital de 16 bits encontrado em CDs tem uma relação máxima de sinal-ruído de 96 dB e sistemas profissionais de áudio digital de 24 bits, chegam até 144 dB. Assim em 2011, a tecnologia digital de conversão de áudio é limitada em um sinal-ruído de cerca de 123 dB ^[11][12][13] (efetivamente 21 bits) por causa das limitações no design de circuitos integrados. ^{[nota 1]} Ainda, isso aproxima a correspondência com a performance da audição humana ^[14][15]. Múltiplos conversores podem ser usados para cobrir diferentes alcances do mesmo sinal, sendo combinados juntos para gravar um amplo alcance dinâmico a longo prazo, enquanto ainda são limitados pelo alcance dinâmico de um único conversor no curto prazo, que é chamado "alcance dinâmico estendido" ^[16][17].

Relação Sinal-Ruído e resolução de profundidade de bits
Quantidade de bits	Relação Sinal-Ruído	Valores possíveis de inteiros por amostra	Alcance por amostra na Base 10 com sinal
4	24,08 dB	16	-8 a +7
8	48,16 dB	256	-128 a +127
11	66,22 dB	2.048	-1.024 a +1.023
12	72,24 dB	4.096	-2.048 a +2.047
16	96,33 dB	65.536	-32.768 a +32.767
18	108,37 dB	262.144	-131.072 a +131.071
20	120,41 dB	1.048.576	-524.288 a +524.287
24	144,49 dB	16.777.216	-8.388.608 a +8.388.607
32	192,66 dB	4.294.967.296	-2.147.483.648 a +2.147.483.647
48	288,99 dB	281.474.976.710.656	-140.737.488.355.328 a +140.737.488.355.327
64	385,32 dB	18.446.744.073.709.551.616	-9.223.372.036.854.775.808 a +9.223.372.036.854.775.807

Vírgula flutuante

A resolução das amostras com vírgula flutuante é menos direta que amostras com inteiros, porque valores racionais não são espaçados igualmente. Em representações com vírgula flutuante, o espaço entre dois valores adjacentes é em proporção ao valor. Isso aumenta significativamente a relação Sinal-Ruído em comparação com um sistema de inteiros porque a precisão de um sinal de alto nível irá ser o mesmo assim como a precisão de um sinal idêntico em um nível mais baixo.

A troca entre vírgula flutuante e inteiros é que o espaço entre valores racionais grandes é maior que o espaço entre inteiros grandes de uma mesma profundidade de bit. Arredondando uma vírgula flutuante grande resulta em um erro muito maior que arredondar uma vírgula flutuante pequena onde arredondar um número inteiro irá sempre resultar no mesmo nível de erro. Em outras palavras, inteiros têm arredondamento que é uniforme, sempre arredondando o último bit significante para 0 ou 1, e vírgula flutuante tem uma relação Sinal-Ruído que é uniforme, o nível de ruído da quantização é sempre uma certa proporção do nível de sinal^[18]. Um ruído de fundo de vírgula flutuante irá aumentar na medida que o sinal aumenta e diminui assim que ele diminui, resultando em variação audível se a profundidade de bit é baixa o suficiente ^[19].

Processamento de áudio

A maioria das operações de processamento em áudio digital envolvem requantização de amostras e portanto introduz erro de arredondamento adicional análogo ao erro de quantização original introduzido durante a conversão analógico-digital. Para evitar erros de arredondamento maiores que o erro implícito durante a conversão A/D, cálculos durante o processamento devem ser feitos com precisão maior que nas amostras de entrada ^[20].

Operações de processamento digital de sinais podem ser feitas em tanto com precisão de vírgula fixa ou vírgula flutuante. Em ambos os casos, a precisão de cada operação é determinada pela precisão das operações do hardware usado para realizar cada etapa do processamento e não da resolução dos dados de entrada. Por exemplo, em processadores x86, operações com vírgula flutuante são feitas com precisão simples ou precisão dupla e operações com vírgula fixa de resolução de 16, 32 ou 64 bit. Consequentemente, todos os processos feitos em hardware baseado da Intel irão ser feitos com estas limitações independente do formato fornecido.

Processadores digitais de sinal com vírgula fixa frequentemente suportam tamanho de palavra específica em função de suportar resolução de sinal específica. Por exemplo, o chip Motorola 56000 usa multiplicadores 24 bits e acumuladores 56 bits para realizar operações de multiplicação acumulativas em duas amostras de 24 bits sem transbordar ou truncar ^[21].

Dither

Para fins de comparação, na imagem acima diversos níveis de Headroom e ruído de fundo em aplicações de áudio (Em Inglês). Gráficos: Som ao vivo, Microfone, Gravação masterizada em 24 bits, CD, Rádio FM, Alto-falante

O ruído introduzido pelo erro de quantização, incluindo erros de arredondamento e perda de precisão introduzida durante o processamento do áudio, pode ser disfarçado adicionando uma pequena quantidade de ruído randômico, chamado "dither" ^{[nota 2]}, para o sinal antes de ser quantizado. O Dithering adiciona este ruído randômico ao sinal para ser quantizado, que mascara os erros de quantização não-linear no final do processo, gerando muita pouca distorção, com um custo de se ter um ruído de fundo a mais, como um chiado muito sutil. Muitos masterizadores, antes de finalizar algum áudio para uma profundidade de bit mais baixa que a de trabalho (para adaptar ao formato que a mídia final suporta), adicionam algum tipo de ruído randômico que pode ser o ruído branco randômico, o ruído RPDF ou TPDF, que são ruídos com distribuição de probabilidade específica.

O Dither recomendado para áudio digital de 16 bit medido utilizando o padrão ITU-R 468, é de cerca de 66 dB abaixo do nível de alinhamento (que é normalmente 0 dBv), ou 84 dB abaixo na escala total digital,^{[nota 3]} a qual é comparável com microfones e ruído de fundo, uma pequena consequência em áudio 16 bit.

Áudio digital em 24 bit não requer dithering, assim como o nível de ruído de um conversor digital é sempre mais alto do que o nível necessário de qualquer dither que pode ser aplicado. Áudio nesta quantidade de bits teoricamente pode codificar 144 dB de alcance dinâmico, mas baseado nos datasheets de fabricantes nenhum conversor A/D existente pode providenciar mais que ~125 dB ^[22].

Dither também pode ser usado para aumentar o alcance dinâmico efetivo. O alcance dinâmico percebido de áudio 16 bit pode ser de 120 dB ou mais com dither modulado, levando vantagem da resposta de frequência da audição humana ^[23][24].

Alcance dinâmico e headroom

Alcance dinâmico é a diferença entre o sinal mais alto e o mais baixo que um sistema pode gravar ou reproduzir. Sem dither, o alcance dinâmico correlata com ruído de fundo da quantização. Por exemplo, a resolução de 16 bits com inteiros permite um alcance dinâmico de 96 dB. Sem a aplicação apropriada do dither, sistemas digitais podem reproduzir sinais com níveis mais baixos do que sua resolução normalmente poderia permitir, estendendo o alcance dinâmico efetivo além do limite imposto pela resolução ^[25]. O uso de técnicas como sobreamostragem (oversampling) e modelamento de ruído podem estender o alcance dinâmico do áudio amostrado movimentando o erro de quantização para fora da banda de frequência de interesse.

Se o nível máximo do sinal é mais baixo do que o permitido pela profundidade de bit, a gravação tem headroom. Usando profundidade de bit maior durante a gravação de estúdio pode fazer o headroom livre enquanto mantém o mesmo alcance dinâmico. Isso reduz o risco de clipping sem aumentar os erros de quantização em baixos volumes.

Sobreamostragem

Sobreamostragem é um método alternativo para aumentar o alcance dinâmico de áudio PCM sem mudar o número de bits por amostra ^[26]. Na sobreamostragem, as amostras de áudio são duplicadas ou mais para a taxa de amostragem desejada. Porque erros de quantização são assumidos para serem uniformemente distribuídos com frequência, muitos dos erros da quantização são deslocados para frequências ultrassônicas e podem ser removidas pelo conversor D/A durante a reprodução de mídia.

Para um aumento equivalente a n bits adicionais de resolução, um sinal deve ser sobreamostrado por

${\displaystyle \mathrm {quantidade\ de\ amostras} =(2^{n})^{2}=2^{2n}.}$

Por exemplo, um conversor D/A de 14 bits pode produzir áudio de 16 bits a 48 kHz se operado com sobreamostragem de 16×, ou 768 kHz. PCM sobreamostrado, entretanto, troca menos bits por amostra para mais amostras em função de obter a mesma resolução.

O alcance dinâmico também pode ser melhorado com sobreamostragem de reconstrução de sinal, sem sobreamostragem na origem. Considere sobreamostragem 16× de reconstrução: Cada amostra de reconstrução pode ser única em que para cada um dos pontos originais na amostra, 16 novos são inseridos, todos tendo sido calculados por um filtro de reconstrução digital. O mecanismo de aumentar efetivamente a profundidade de bit foi previamente discutido, que é, ruído de quantização não diminui, mas o espectro do ruído se espalha 16× da largura de banda do áudio.

Nota histórica: O padrão dos CDs foi desenvolvido pela colaboração entre a Sony e a Philips. O primeiro aparelho da Sony tinha um conversor D/A de 16 bits; e o primeiro da Philips tinha dois conversores D/A de 14 bits. Isso causou confusão no mercado e em meios profissionais. Anos depois, um dos jornais de engenharia comercial erroneamente fez uma nota histórica do conversor D/A de 14 bits no dispositivo da Philips que permitia 84 dB SNR, o escritor ou tinha desconhecimento das especificações do aparelho que indicava 4× de sobreamostragem ou desconhecimento da implicação. Isso foi corretamente notado que a Philips não tinha originalmente fornecido conversores D/A de 16 bits na época, mas o escritor não tinha conhecimento do poder do processamento digital de sinal para aumentar a SNR para 90 dB ^[27].

Aplicações

Profundidade de bit é uma propriedade fundamental de implementações de áudio digital. Dependendo dos requerimentos da aplicação e capacidade do equipamento, diferentes profundidades de bit são usadas para diferentes usos.

Aplicações de exemplo e profundidade de bit suportadas

Applicação	Descrição	Formato(s) de áudio
CD de áudio[nota_abaixo 1]	Mídia digital	16 bits LPCM
DVD de áudio[28]	Mídia digital	16, 20 e 24 bits LPCM[nota_abaixo 2]
CD de super áudio[29]	Mídia digital	1 bit Direct Stream Digital (PDM - Modulação por Densidade de Pulsos)
Disco Blu-ray de Áudio[30]	Mídia digital	16, 20 e 24 bits LPCM e outros[nota_abaixo 3]
Fita DV de áudio[31]	Mídia digital	12 e 16 bits PCM não comprimidos
Setor de Normatização das Telecomunicações Recomendação G.711[32]	Padrão de compressão para telefonia	8 bits PCM com compansão[nota_abaixo 4]
NICAM-1, NICAM-2, e NICAM-3[33]	Padrões de compressão para radiodifusão	10, 11 e 10 bits PCM respectivamente, com compansão[nota_abaixo 5]
Ardour	Estação de trabalho digital criada por Paul Davis e comunidade da Ardour	32 bits com vírgula flutuante[34]
Pro Tools 11	Estação de trabalho digital da Avid	Sessões de 16 e 24 bits ou 32 bits com vírgula flutuante e mixagem 64 bits com vírgula flutuante[35]
Logic Pro X	Estação de trabalho digital da Apple	Projetos em 16 e 24 bits e mixagem em 32 ou 64 bits com vírgula flutuante[36]
Ableton Live[37]	Estação de trabalho digital da Ableton	Profundidade de bit em 32 bits e somatória em 64 bits
Reason 7	Estação de trabalho da Propellerhead Software	E/S de 16, 20 e 24 bits, aritmética em 32 bits com vírgula flutuante, e somatória em 64 bits[38]
REAPER 5	Estação de trabalho digital da Cockos.	Renderização em 8, 16, 24 e 32 bits PCM, 32 e 64 bits com vírgula flutuante, IMA ADPCM 4 bits e 2 bits cADPCM Mixagem em 8, 16, 24 e 32 bits, 32 e 64 bits com vírgula flutuante
GarageBand 2011 (Versão 6)	Estação de trabalho digital da Apple	Padrão em 16 bits com gravação de instrumentos reais em 24 bits[39]
Audacity	Editor de áudio de código aberto	16 e 24 bits LPCM e 32 bits com vírgula flutuante[40]
FL Studio	Estação de trabalho digital da Image Line	16 e 24 bits e 32 bits com vírgula flutuante (controlado pelo O.S.)[41]

1. «(Em Inglês) - Sweetwater Knowledge Base, Masterlink: What is a "Red Book" CD?». www.sweetwater.com. Sweetwater. 27 Abril 2007. Consultado em 25 agosto 2013 
2. DVD de áudio também suporta Meridian Lossless Packing, uma técnica de compressão sem perdas.
3. Bluray suporta uma variedade de formatos não-LPCM mas todos se adaptam para alguma combinação de 16, 20 ou 24 bits por amostra.
4. O setor especifica os algoritmos de compansão A-law e μ-law , que comprimem de 13 e 14 bits respectivamente.
5. Sistemas NICAM 1, 2 e 3 comprimem de 13, 14 e 14 bits respectivamente.

Bit rate e tamanho de arquivo

Profundidade de bit afeta o bit rate e o tamanho de arquivo. Bits são a unidade básica de dados usada em computação e comunicação digital. Bit rate refere-se à quantidade de dados, especificamente bits transmitidos ou recebidos por segundo. Em MP3 e outros formatos com compressão, bit rate descreve a quantidade de dados usados para codificar um sinal de áudio digital. Normalmente medido em kb/s ^[42]

Ver também

• Profundidade de cor, conceito semelhante para imagens digitais
• Som digital
• Processamento de sinal analógico

Notas

1. Enquanto conversores 32 bits existem, eles são apenas para propostas de marketing e não têm nenhum benefício prático sobre os conversores de 24 bits; os bits extras são tanto zero ou codificam apenas ruído. Links:
   «(Em Inglês) - The great audio myth: why you don't need that 32-bit DAC». Android Authority (em inglês). So your 32-bit DAC is actually only ever going to be able to output at most 21-bits of useful data and the other bits will be masked by circuit noise. 
   «(Em Inglês) - 32-bit capable DACs». hydrogenaud.io. all the '32 bit capable' DAC chips existent today have actual resolution less than 24 bit. 
2. Leia no artigo sobre dither em imagens digitais para entender a analogia com áudio digital também
3. Escala total digital é todo valor analógico que pode ser representado. Por exemplo, áudio 16 bit é centralizado no valor 0, e pode conter valores desde -32.768 a +32.767. Um sinal que esteja em toda sua amplitude atinge estes valores. Em estações de trabalho de áudio frequentemente utilizam aritmética de vírgula flutuante, a qual pode incluir valores além da escala total, para evitar clipping no processamento do áudio. Em uma representação de vírgula flutuante, um sinal em ampla escala normalmente é definido para atingir desde -1,0 a +1,0.

Referências

1. Thompson, Dan (2005). (Em Inglês) - Understanding Audio. São Paulo: Berklee Press. ISBN 978-0-634-00959-4 
2. Campbell, Robert (2013). (Em Inglês) - Pro Tools 10 Advanced Music Production Techniques. [S.l.]: Cengage Learning. p. 247 
3. Wherry, Mark (Março 2012). «(Em Inglês) - Avid Pro Tools 10». Sound On Sound 
4. Price, Simon (Outubro 2005). «(Em Inglês) - Reason Mixing Masterclass». Sound On Sound 
5. «(Em Inglês) - Ableton Reference Manual Version 10, 32. Audio Fact Sheet». Ableton. 2019 
6. Kabal, Peter (3 Janeiro 2011). «(Em Inglês) - Audio File Format Specifications, WAVE Specifications». McGill University 
7. Kabal, Peter (3 Janeiro 2011). «(Em Inglês) - Audio File Format Specifications, AIFF / AIFF-C Specifications». McGill University 
8. Smith, Steven (1997). «(Em Inglês) - The Scientist and Engineer's Guide to Digital Signal Processing, Chapter 4 – DSP Software / Floating Point (Real Numbers)». www.dspguide.com 
9. Sinal analógico#Digitalização
10. Kester, Walt (2007). «(Em Inglês) - Taking the Mystery out of the Infamous Formula, "SNR = 6.02N + 1.76dB," and Why You Should Care» (PDF). Analog Devices Inc. 
11. Nwavguy (6 de setembro de 2011). «(Em Inglês) - NwAvGuy: Noise & Dynamic Range». NwAvGuy. 24 bit DACs often only manage approximately 16 bit performance and the very best reach 21 bit (ENOB) performance. 
12. «(Em Inglês - PCM4222». Dynamic Range (–60dB input, A-weighted): 124dB typical Dynamic Range (–60dB input, 20 kHz Bandwidth): 122dB typical 
13. «WM8741 : High Performance Stereo DAC». Cirrus Logic. 128dB SNR (‘A’-weighted mono @ 48 kHz) 123dB SNR (non-weighted stereo @ 48 kHz) 
14. D. R. Campbell. «(Em Inglês) - Aspects of Human Hearing» (PDF). Cópia arquivada (PDF) em 21 Agosto 2011. The dynamic range of human hearing is [approximately] 120 dB 
15. «(Em Inglês) - Sensitivity of Human Ear». Cópia arquivada em 4 Junho 2011. The practical dynamic range could be said to be from the threshold of hearing to the threshold of pain [130 dB] 
16. [1], "Multiple A to D converters for enhanced dynamic range" 
17. Christodoulou, Lakis; Lane, John; Kasparis, Takis (1 de março de 2010). «Dynamic range extension using multiple A/D converters». 2010 4th International Symposium on Communications, Control and Signal Processing (ISCCSP): 1–4. doi:10.1109/ISCCSP.2010.5463427 
18. Steven Smith (1997). «(Em Inglês) - The Scientist and Engineer's Guide to Digital Signal Processing, Chapter 4 – DSP Software / Floating Point (Real Numbers)». www.dspguide.com 
19. James Moorer (Setembro 1999). «(Em Inglês) - 48-Bit Integer Processing Beats 32-Bit Floating-Point for Professional Audio Applications» (PDF). www.jamminpower.com 
20. John Tomarakos. «(Em Inglês) - Relationship of Data Word Size to Dynamic Range and Signal Quality in Digital Audio Processing Applications». www.analog.com. Analog Devices Inc. 
21. «DSP56001A» (PDF). Freescale 
22. (Em Inglês) - Choosing a high-performance audio ADC 
23. Montgomery, Chris (25 Março 2012). «(Em Inglês) - 24/192 Music Downloads ...and why they make no sense». xiph.org. Cópia arquivada em 7 Julho 2013. With use of shaped dither, which moves quantization noise energy into frequencies where it's harder to hear, the effective dynamic range of 16 bit audio reaches 120dB in practice, more than fifteen times deeper than the 96dB claim. 120dB is greater than the difference between a mosquito somewhere in the same room and a jackhammer a foot away.... or the difference between a deserted 'soundproof' room and a sound loud enough to cause hearing damage in seconds. 16 bits is enough to store all we can hear, and will be enough forever. 
24. Stuart, J. Robert (1997). «(Em Inglês) - Coding High Quality Digital Audio» (PDF). Meridian Audio Ltd. Cópia arquivada (PDF) em 7 Abril 2016. One of the great discoveries in PCM was that, by adding a small random noise (that we call dither) the truncation effect can disappear. Even more important was the realisation that there is a right sort of random noise to add, and that when the right dither is used, the resolution of the digital system becomes infinite. 
25. «(Em inglês) - Dithering in Analog-to-Digital Conversion» (PDF). e2v Semiconductors. 2007. Cópia arquivada (PDF) em 4 Outubro 2011 
26. Kester, Walt. «(Em Inglês) - Oversampling Interpolating DACs» (PDF). Analog Devices 
27. http://www.hifiengine.com/manual_library/philips/cd100.shtml
28. «(Em inglês) - Understanding DVD-Audio» (PDF). Sonic Solutions. Consultado em 25 Agosto 2013. Cópia arquivada (PDF) em 4 Março 2012 
29. Shapiro, L. (2 Julho 2001). «(Em inglês) - Surround Sound, Page 10». ExtremeTech. Consultado em 26 Agosto 2013 
30. «(Em Inglês) - White paper Blu-ray Disc Format, 2.B Audio Visual Application Format Specifications for BD-ROM Version 2.4» (PDF). Blu-ray Disc Association. Abril 2010. Consultado em 25 Agosto 2013 
31. Puhovski, Nenad (Abril 2000). «(Em Inglês) - DV – A SUCCESS STORY». www.stanford.edu. Consultado em 26 Agosto 2013. Cópia arquivada em 27 Outubro 2004 
32. «G.711 : Pulse code modulation (PCM) of voice frequencies» (PDF). International Telecommunications Union. Consultado em 25 Agosto 2013 
33. «(Em Inglês) - DIGITAL SOUND SIGNALS: tests to compare the performance of five companding systems for high-quality sound signals» (PDF). BBC Research Department. Agosto 1978. Consultado em 26 Agosto 2013. Cópia arquivada (PDF) em 8 Novembro 2012 
34. «(Em Inglês) - Ardour Key Features». Ardour Community. 2014. Consultado em 8 Abril 2014 
35. «(Em Inglês) - Pro Tools Documentation, Pro Tools Reference Guide» (ZIP/PDF). Avid. 2013. Consultado em 26 Agosto 2013 
36. «(Em Inglês) - Logic Pro X: User Guide» (PDF). Apple. Janeiro 2010. Consultado em 26 Agosto 2013 
37. «(Em Inglês) - Ableton Reference Manual Version 10, 32. Audio Fact Sheet». Ableton. 2019. Consultado em 3 setembro 2019 
38. «(Em Inglês) - Reason 7 Operation Manual» (PDF). Propellerhead Software. 2013. Consultado em 26 Agosto 2013. Cópia arquivada (PDF) em 24 Maio 2013 
39. «GarageBand '11: Set the audio resolution». Apple. 13 Março 2012. Consultado em 26 Agosto 2013 
40. «(Em Inglês) - Audacity: Features». wiki.audacityteam.com. Audacity development team. Consultado em 13 setembro 2014 
41. «(Em Inglês) - Audio Settings». www.image-line.com. Consultado em 12 de fevereiro de 2019 
42. «(Em Inglês) - Sample Rate, Bit-Depth & Bitrate | Exclusivemusicplus». 26 de outubro de 2018