Terceiro problema de Hilbert
Na matemática, o terceiro problema de Hilbert foi proposto por David Hilbert em 1900, sendo esse um dos seus 23 problemas. Esse problema consiste em provar que, se dois poliedros têm o mesmo volume, então é possível decompor um deles em outros poliedros menores e reconstruir estes poliedros formando o outro. Hilbert supôs que a resposta para o problema seria negativa. Este problema foi resolvido por seu aluno Max Dehn.
Motivação
[editar | editar código-fonte]Conforme explicou Hilbert:[1]
- Em duas cartas a Gerling, Gauss mostrou-se preocupado que alguns teoremas da geometria dos sólidos dependiam do método da exaustão, ou, na nomenclatura moderna, no axioma da continuidade (ou no axioma de Arquimedes). Gauss menciona, em particular, o teorema demonstrado por Euclides, que duas pirâmides de mesma altura estão para si como suas bases. O problema análogo para a geometria plana foi resolvido. Gerling também teve sucesso ao provar a igualdade de volume para poliedros simétricos, dividindo-os em partes congruentes. Apesar disto, parece ser provável que uma prova genética deste teorema de Euclides seja impossível. Isto seria resolvido ao se exibir dois tetraedros de mesma base e mesma altura, mas que não possam ser quebrados em tetraedros congruentes, e que não possam ser combinados com tetraedros congruentes para formar poliedros que possam, estes, serem quebrados em tetraedros congruentes.
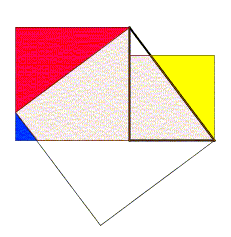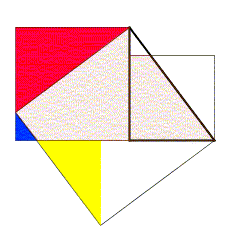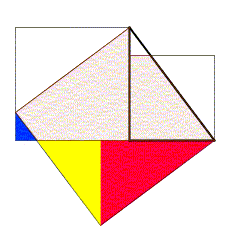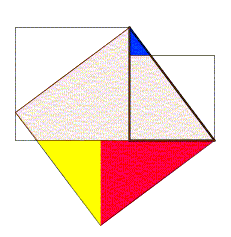
Euclides havia demonstrado o teorema de Pitágoras através de uma decomposição deste tipo: a partir de dois quadrados, cujos lados eram os catetos do triângulo retângulo, Euclides cortou a figura e remontou, formando um quadrado cujo lado é a hipotenusa.[2]
Esta propriedade pode ser chamada de congruência por tesoura (no original, scissors congruence), ou seja, dois polígonos (ou poliedros) P e Q são congruentes quando é possível decompor ambos e , onde a união é disjunta a menos de uma aresta ou menos (no caso dos polígonos) ou face ou menos (no caso dos poliedros) e os elementos de mesmo índice são congruentes. Em outras palavras, é como se uma das figuras fosse cortada e rearrumada para formar a outra.[2][3]
O Teorema de Bolyai-Gerwien, de 1833, mostrou que a congruência por tesoura é equivalente a dois polígonos terem a mesma área, ou seja:[2]
- Dois polígonos que tem a mesma área são congruentes por tesoura
Enunciado
[editar | editar código-fonte]Uma decomposição de um poliedro P é uma coleção finita de poliedros P1, P2, ... Pn cuja união é P, e cuja interseção, par a par, é formada apenas de faces, arestas ou vértices.[2][Nota 1]
Dois poliedros P e Q são congruentes por tesoura quando existem decomposições P1, P2, ... Pn e Q1, Q2, ... Qn, respectivamente, de P e Q, tal que cada Pi é congruente a Qi.[2]
A pergunta de Hilbert, então, para a qual ele esperava uma resposta negativa, era:[2]
- Suponha que o volume de P seja igual ao volume de Q. É possível mostrar que P e Q são congruentes por tesoura?
Solução de Max Dehn: condição necessária
[editar | editar código-fonte]Max Dehn, aluno de Hilbert, resolveu este problema em 1902[2] (ou 1900 e 1901).[3] A demonstração envolveu a construção de um novo invariante, que foi denominado invariante de Dehn, e que envolve uma conta sobre os ângulos diedros e comprimentos das arestas, calculados sobre as arestas do poliedro.[2][3][4]
Este invariante, δ não é alterado através da decomposição e recomposição. Porém, para um tetraedro regular e um cubo, de mesmo volume, temos diferentes valores para o invariante de Dehn.[2][3]
Condição suficiente
[editar | editar código-fonte]Em 1965, Sydler mostrou que o invariante de Dehn é, também, condição suficiente para dois poliedros serem congruentes por tesoura, ou seja, se dois poliedros tem o mesmo volume e o mesmo invariante de Dehn, então é possível decompor um deles e remontar o outro.[2][3]
Notas
[editar | editar código-fonte]- ↑ O texto de Champanerkar esqueceu de mencionar o caso do vértice.
Referências
- ↑ David Hilbert, citado por J. Gray, The Hilbert Challenge, Oxford University Press, New York, 2000, citado em Hilbert's 3rd problem.
- ↑ a b c d e f g h i j Abhijit Champanerkar, College of Staten Island CUNY, Scissors Congruence & Hilbert's 3rd Problem [em linha]
- ↑ a b c d e Vladik Kreinovich, Equidecomposability (scissors congruence) of polyhedra in R3 and R4 is algorithmically decidable: Hilbert's 3rd problem revisited [em linha]
- ↑ J. Gray, The Hilbert Challenge, Oxford University Press, New York, 2000.

