Compus de opt octaedre cu libertate de rotație
| Compus de opt octaedre cu libertate de rotație | |
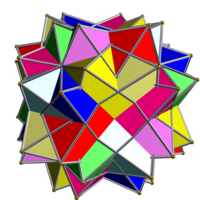 | |
| Descriere | |
|---|---|
| Tip | compus uniform UC10 - UC11 - UC12 |
| Fețe | 64 (triunghiuri) |
| Laturi (muchii) | 96 |
| Vârfuri | 48 |
| Configurația vârfului | 3.3.3.3[1] |
| Configurația feței | V4.4.4 |
| Grup de simetrie |
|
| Volum | ≈3,771 a3 (a = latura) |
| Proprietăți | Constituenți: 8 octaedre |
| Figura vârfului | |
 | |
În geometrie compusul de opt octaedre cu libertate de rotație este un compus poliedric uniform realizat dintr-un aranjament simetric de 8 octaedre, considerate ca antiprisme triunghiulare.[2]
Are indicele de compus uniform UC11.[2]
Construcție
[modificare | modificare sursă]Poate fi construit prin suprapunerea a opt octaedre identice și apoi rotirea lor în perechi în jurul celor patru axe care trec prin centrele a două fețe opuse ale octaedrului. Fiecare octaedru este rotit cu un unghi egal (și opus, într-o pereche) θ.
Poate fi construit prin suprapunerea a doi compuși de patru octaedre cu libertate de rotație, unul rotit cu unghiul θ, iar celălalt rotit cu unghiul −θ.
Când θ = 0, toate cele opt octaedre coincid. Când θ este de 60°, octaedrele coincid în perechi dând două copii suprapuse ale compusului de patru octaedre.
Mărimi asociate
[modificare | modificare sursă]Coordonate carteziene
[modificare | modificare sursă]Coordonatele carteziene ale vârfurilor acestui compus sunt toate permutările lui
Volum
[modificare | modificare sursă]Următoarea formulă pentru volum V este stabilită pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:
Imagini
[modificare | modificare sursă]- Compus de opt octaedre cu libertate de rotație
-
Compusul cu θ = 0°
-
Compusul cu θ = 5°
-
Compusul cu θ = 10°
-
Compusul cu θ = 15°
-
Compusul cu θ = 20°
-
Compusul cu θ = 25°
-
Compusul cu θ = 30°
-
Compusul cu θ = 35°
-
Compusul cu θ = 40°
-
Compusul cu θ = 45°
-
Compusul cu θ = 50°
-
Compusul cu θ = 55°
-
Compusul cu θ = 60°
Note
[modificare | modificare sursă]Vezi și
[modificare | modificare sursă]- Compuși de octaedre
- Compus de trei octaedre
- Compus de patru octaedre
- Compus de patru octaedre cu libertate de rotație
- Compus de cinci octaedre
- Compus de șase octaedre
- Compus de zece octaedre
- Compus de douăzeci de octaedre
- Compus de douăzeci de octaedre cu libertate de rotație














