Dodecagramă

Dodecagramă regulată
Tip	figură poligonală regulată
Laturi și vârfuri	12
Simbol Schläfli	{12/5}
Diagramă Coxeter
Grup de simetrie	Diedrală (D12), ordin 24
Unghi interior (grade)	30°
Proprietăți	poligon stelat, echilateral, izogonal, izotoxal

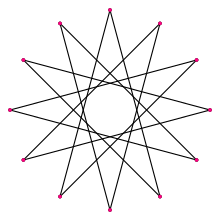
În geometrie o dodecagramă este un poligon stelat cu douăsprezece vârfuri,^[1] cu simbolul Schläfli {12/5}.

Denumirea dodecagramă combină prefixul numeric dodeca-^[2] cu sufixul -gramă, care derivă din greacă γραμμῆ, care înseamnă o dreaptă.^[3]

Există și 4 compuși regulați: {12/2}, {12/3}, {12/4} și {12/6}.

Dodecagrama regulată

Există o singură formă regulată: {12/5}, care are 12 vârfuri, cu pasul stelării de 5. O dodecagramă regulată are același aranjament al vârfurilor ca un dodecagon regulat {12}, care poate fi considerat drept {12/1}.

Compuși dodecagramici regulați

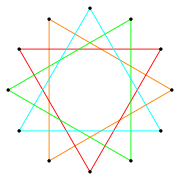
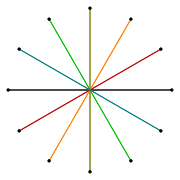
Există patru compuși regulați: {12/2} = 2{6}, {12/3} = 3{4}, {12/4} = 4{3} și {12/6} = 6{2}. Primul este un compus de două hexagoane, al doilea este un compus de trei pătrate, al treilea este un compus din patru triunghiuri, iar cel al patrulea este un compus din șase digoane cu laturi drepte. Ultimele două pot fi considerate compuși de două hexagrame, iar ultimul drept compus de trei compuși de tetragrame.

• 
  2{6}
• 
  3{4}
• 
  4{3}
• 
  6{2}

Dodecagramele ca figuri izotoxale

Un poligon izotoxal (tranzitiv pe laturi) are două vârfuri și un singur tip de latură în clasa sa de simetrie. Există 5 stele dodecagramice izotoxale cu un grad de libertate al unghiurilor, care alternează vârfuri aflate pe două raze, una simplă, 3 compuși și o stea cu un parcurs unic.

Dodecagrame izotoxale

Tip	Simplă	Compuși			Stea
Densitate	1	2	3	4	5
Imagine	{(6)α}	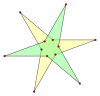2{3α}	3{2α}	2{(3/2)α}	{(6/5)α}

Dodecagramele ca figuri izogonale

O dodecagramă regulată poate fi văzută ca un hexagon cvasitrunchiat, t{6/5} = {12/5}. Alte variante izogonale (tranzitive pe vârfuri) cu vârfuri egal distanțate pot fi construite cu două lungimi de laturi.

t{6}

t{6/5} = {12/5}

Graful complet

Suprapunerea tuturor dodecagoanelor și dodecagramelor — inclusiv degeneratul compus din șase digoane {12/6} — produce graful complet K₁₂.

K₁₂

negru: cele douăsprezece vârfuri (noduri) roșu: {12} dodecagon regulat verde: {12/2} = 2{6} două hexagoane albastru: {12/3} = 3{4} trei pătrate azuriu: {12/4} = 4{3} patru triunghiuri violet: {12/5} dodecagramă obișnuită galben: {12/6} = 6{2} șase digoane

Dodecagrame regulate în poliedre

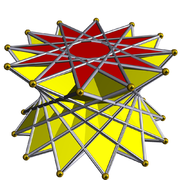
Dodecagramele pot să apară în poliedrele uniforme. Mai jos sunt cele trei poliedre prismatice uniforme care au fețe în formă de dodecagrame regulate (nu există alte poliedre uniforme care conțin dodecagrame).

• 
  Prismă dodecagramică
• 
  Antiprismă dodecagramică
• 
  Retroprismă dodecagramică

Dodecagramele pot să apară și în teselările stelate ale planului euclidian.

Simbolismul dodecagramelor

Steaua cu douăsprezece colțuri este o trăsătură proeminentă a vechilor tobe Dong Son vietnameze

Exemple când dodecagrame sau stele cu douăsprezece colțuri au fost folosite ca simboluri:

• Cele douăsprezece triburi ale lui Israel în iudaism.^[4]
• Cei Doisprezece Apostoli în creștinism^[5]
• Cei Doisprezece Olimpieni în politeismul elenic^[6]
• Cele 12 semne ale zodiacului^[7]

Note

1. en „Between a square rock and a hard pentagon: Fractional polygons”. 28 septembrie 2017. 
2. „dodeca” la DEX online
3. en Liddell, Henry George; Scott, Robert (1940), A Greek-English Lexicon: γραμμή, Oxford: Clarendon Press 
4. en Ancient Jewish History: The twelve tribes of Israel, in Judaism, jewishvirtuallibrary.org, accesat 2023-11-29
5. en 12-Point Star, religionfacts.com, arhivat, accesat 2023-11-29
6. en 12 Greek Gods and Godesses, britannica.com, accesat 2023-11-29
7. en Gott's Symbols, gottssymbols.tumblr.com, accesat 2023-11-29

Bibliografie

• en Eric W. Weisstein, Dodecagram la MathWorld.
• en Grünbaum, B. and G.C. Shephard; Tilings and Patterns, New York: W. H. Freeman & Co., (1987), ISBN: 0-7167-1193-1.
• en Grünbaum, B.; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993), ed T. Bisztriczky et al., Kluwer Academic (1994) pp. 43–70.
• en John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN: 978-1-56881-220-5 (Chapter 26. pp. 404: Regular star-polytopes Dimension 2)

Legături externe

Portal Matematică

• Materiale media legate de dodecagramă la Wikimedia Commons