Dualitate (matematică)

În matematică, o dualitate transformă concepte, teoreme sau structuri matematice în alte concepte, teoreme sau structuri, printr-o transformare „unu la unu”, adesea (dar nu întotdeauna) prin intermediul unei operații de involuție:dacă dualul lui A este B, atunci dualul lui B este A. Astfel de involuții au uneori puncte fixe, astfel încât dualul lui A este A însuși. De exemplu, teorema lui Desargues este autoduală în acest sens pentru dualitatea standard în geometria proiectivă.

Termenul dualitate are mai multe înțelesuri.^[1] A fost descris ca „un concept foarte răspândit și important în matematică (modernă)”^[2] și "o temă generală importantă care are manifestări în aproape toate domeniile matematicii".^[3]

Multe dualități matematice între obiecte de două tipuri se referă la împerecheri, aplicații biliniare de la un obiect de un tip și un alt obiect de al doilea tip la vreo familie de scalari.De exemplu, dualitatea în algebra liniară corespunde aplicațiilor biliniare pe împerecheri de spații vectoriale și scalari, dualitatea dintre distribuții și funcțiile de testare asociate corespunde împerecherii dintre o distribuție și funcția de testare, iar dualitatea Poincaré corespunde în mod similar la numărul de intersecții, privit ca o împerechere între subvarietăți ale unei varietăți date.^[4]

Din punct de vedere al teoriei categoriilor, dualitatea poate fi văzută și ca un functor, cel puțin în domeniul spațiilor vectoriale. Acest functor atribuie fiecărui spațiu spațiul său dual,iar produsul fibrat atribuie fiecărei săgeți f: V → W dualul său f^∗: W^∗ → V^∗.

Exemple introductive

După Michael Atiyah,

„În matematică dualitatea nu este o teoremă, ci un „principiu”.^[5]”

Următoarea listă de exemple arată trăsăturile comune ale multor dualități, dar indică și faptul că semnificația exactă a dualității poate varia de la caz la caz.

Complementul unei submulțimi

O dualitate simplă, poate cea mai simplă, apare din considerarea submulțimilor unei mulțimi fixe S. Pentru orice submulțime A ⊆ S, complementul A^c este format din toate acele elemente din S care nu sunt conținute în A. Este din nou o submulțime a lui S. Complementarea are următoarele proprietăți:

• Aplicând-o de două ori se revine la mulțimea inițială, adică (A^c)^c = A. Se spune că operația de complementare dublă este o involuție.
• Relația de incluziune A ⊆ B se orientează în diresția inversă B^c ⊆ A^c.
• Fiind date două submulțimi A și B ale S, A este inclusă în B^c dacă și numai dacă B este inclusă în A^c.

Această dualitate apare în topologie ca o dualitate între mulțimi deschise și închise ale unor spații topologice fixe X: o submulțime U a X este închisă dacă și numai dacă complementul său din X este deschis. Din această cauză, multe teoreme despre mulțimi închise sunt duale cu teoremele despre mulțimi deschise. De exemplu, orice reuniune de mulțimi deschise este deschisă, deci dual, orice intersecție de mulțimi închise este închisă. Interiorul unei mulțimi U este cea mai mare mulțime deschisă conținută în aceasta, iar închiderea mulțimii este cel mai mic set închis pe care îl conține. Datorită dualității, complementul interiorului oricărei mulțimii U este în U egal cu închiderea U.

Alte exemple sunt conul dual din geometrie, spațiul vectorial dual din algebra liniară și dualitatea din teoria lui Galois.

Dualități în ordini reversibile

Diagrama Hasse a submulțimilor mulțimii {1,2,3,4}, ordonată parțial prin ⊂. Mulțimea duală, ordonată prin ⊃, se obține întorcând diagrama cu susul în jos. Nodurile verzi formează mulțimea al cărei dual este cea formată din nodurile albe

Fie o mulțime parțial ordonată P = (X, ≤) (o mulțime care are o anumită ordonare, dar nu este necesar ca fiecare element dintr-o pereche să fie ordonat față de celălalt), mulțimea parțial ordonată duală P^d = (X, ≥) este formată din aceleași elemente, dar ordonate invers. Exemple obișnuite de mulțimi parțial ordonate duale sunt

• Relațiile ⊂ și ⊃ ale submulțimilor și supermulțimilor oricărei colecții de mulțimi, cum ar fi submulțimile mulțimii fixe S. Asta corespunde This gives rise to the first example of a duality primului exemplu de dualitate prezentat mai sus;
• operațiile de înmulțire și împărțire (care nu dă rest) în numere întregi.
• Noțiunile de descendent și ascendent în relațiile de rudenie din mulțimea oamenilor.

O transformare duală este un antiautomorfism involutiv f al unei mulțimi parțial ordonate S, adică o involuție de inversare a ordinii f : S → S.^[6][7] În câteva cazuri importante, aceste proprietăți simple determină transformarea în mod unic până la unele simetrii simple.

În topologie, mulțimile deschise și închise sunt noțiuni duale. În teoria matroizilor, familia mulțimilor complementare mulțimilor independente ale unui matroid dat formează ea însăși un matroid, matroidul dual.

Dualități în inversarea dimensională

n-fețele unui cub și ale octaedrului său dual corespund „unu la unu” inversând ordinea dimensiunilor.

Există multe dualități distincte, dar legate între ele, în care obiectele geometrice sau topologice corespund cu alte obiecte de același tip, dar cu o inversare a dimensiunilor elementelor obiectelor. Un exemplu clasic în acest sens este dualitatea corpurilor lui Platon, în care cubul și octaedrul formează o pereche duală, dodecaedrul și icosaedrul formează altă pereche duală, iar tetraedrul este autodual. Poliedrul dual al oricăruia dintre aceste poliedre poate fi format din anvelopa convexă a punctelor centrale ale fiecărei fețe a primului poliedru, astfel încât vârfurile dualului corespund cu fețele primului. Similar, fiecare latură a dualului corespunde unei laturi a primului și fiecare față a dualului corespunde unui vârf al primului. Aceste corespondențe conservă incidența: dacă două părți ale primului poliedru se ating, la fel se ating și cele două elemente corespunzătoare ale poliedrului dual. Mai general, orice politop convex corespunde unui politop dual, cu elementele i-dimensionale a unui politop n-dimensional corespunzând elementelor (n − i − 1)-dimensionale ale politopului dual. Natura conservării incidenței la duale se reflectă în faptul că laticele fețelor politopurilor și ale dualelor lor sunt ele însele teoretic duale. Dualitatea politopurilor și a ordonării sunt ambele involuții: politopul dual al politopului dual al oricărui politop este politopul inițial, iar prin inversarea tuturor relațiilor de ordine de două ori se revine la ordinea inițială. Politopurile duale pot fi geometric diferite, dar toate dualele au aceeași structură combinatorică.

Un graf plan cu albastru și dualul său cu roșu

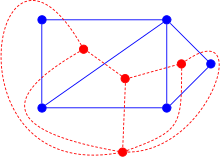
Pentru orice poliedru tridimensional, se poate trasa un graf plan, graful vârfurilor și laturilor sale. Poliedrul dual are un graf dual, un graf cu un vârf pentru fiecare față a poliedrului și o latură pentru fiecare două fețe adiacente. Acest concept de dualitate a grafului plan poate fi generalizat la grafurile plane ale politopurilor din dimensiuni superioare.

Un fel de dualitate geometrică apare și în teoria optimizării, dar nu una care inversează dimensiunile. O problemă de programare liniară poate fi definită de un sistem de variabile reale (coordonatele unui punct din spațiul euclidian ${\displaystyle \mathbb {R} ^{n}}$), un sistem de constrângeri liniare (specificând că punctul se află într-un anumit semispațiu; intersecția acestor semispații este un politop convex, regiunea fezabilă a soluțiilor problemei) și o funcție liniară care indică optimizarea. Fiecare problemă de programare liniară are o problemă duală cu aceeași soluție optimă, dar variabilele din problema duală corespund constrângerilor din problema primară iar constrângerile variabilelor.

Note

1. Atiyah 2007, p. 1.
2. en Kostrikin 2001, Acest citat este prima propoziție din secțiunea finală denumită „comentarii” din acest document.
3. Gowers 2008, p. 187, col. 1.
4. Gowers 2008, p. 189, col. 2.
5. Atiyah 2007, p. 1 (Duality in mathematics is not a theorem, but a "principle".).
6. Artstein-Avidan & Milman 2007.
7. Artstein-Avidan & Milman 2008.

Bibliografie și lectură suplimentară

Dualitate în general

• en Atiyah, Michael (2007), Duality in Mathematics and Physics, lecture notes from the Institut de Matematica de la Universitat de Barcelona (IMUB).
• en Kostrikin, A. I. (2001), „Duality”, În Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104 .
• en Gowers, Timothy (2008), „III.19 Duality”, The Princeton Companion to Mathematics, Princeton University Press, pp. 187–190 .
• en Cartier, Pierre (2001), „A mad day's work: from Grothendieck to Connes and Kontsevich. The evolution of concepts of space and symmetry”, American Mathematical Society. Bulletin. New Series, 38 (4): 389–408, doi:10.1090/S0273-0979-01-00913-2 , ISSN 0002-9904, MR 1848254  (a non-technical overview about several aspects of geometry, including dualities)

Dualitate în topologia algebrică

• en James C. Becker and Daniel Henry Gottlieb, A History of Duality in Algebraic Topology

Dualități particulare

• en Artstein-Avidan, Shiri; Milman, Vitali (2008), „The concept of duality for measure projections of convex bodies”, Journal of Functional Analysis, 254 (10): 2648–66, doi:10.1016/j.jfa.2007.11.008 . Also author's site.
• en Artstein-Avidan, Shiri; Milman, Vitali (2007), „A characterization of the concept of duality”, Electronic Research Announcements in Mathematical Sciences, 14: 42–59, arhivat din original la 24 iulie 2011, accesat în 30 mai 2009 . Also author's site.
• en Dwyer, William G.; Spaliński, Jan (1995), „Homotopy theories and model categories”, Handbook of algebraic topology, Amsterdam: North-Holland, pp. 73–126, MR 1361887, arhivat din original la 9 februarie 2021, accesat în 29 ianuarie 2021 
• en Fulton, William (1993), Introduction to toric varieties, Princeton University Press, ISBN 978-0-691-00049-7 
• en Griffiths, Phillip; Harris, Joseph (1994), Principles of algebraic geometry, Wiley Classics Library, New York: John Wiley & Sons, ISBN 978-0-471-05059-9, MR 1288523 
• en Hartshorne, Robin (1966), Residues and Duality, Lecture Notes in Mathematics, 20, Springer-Verlag, pp. 20–48, ISBN 978-3-540-34794-1 
• en Hartshorne, Robin (1977), Algebraic Geometry, Springer-Verlag, ISBN 978-0-387-90244-9, MR 0463157, OCLC 13348052 
• en Iversen, Birger (1986), Cohomology of sheaves, Universitext, Springer-Verlag, ISBN 978-3-540-16389-3, MR 0842190 
• en Joyal, André; Street, Ross (1991), „An introduction to Tannaka duality and quantum groups” (PDF), Category theory, Lecture Notes in Mathematics, 1488, Springer-Verlag, pp. 413–492, doi:10.1007/BFb0084235, ISBN 978-3-540-46435-8, MR 1173027 
• en Lam, Tsit-Yuen (1999), Lectures on modules and rings, Graduate Texts in Mathematics, 189, Springer-Verlag, ISBN 978-0-387-98428-5, MR 1653294 
• en Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211, Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556 
• en Loomis, Lynn H. (1953), An introduction to abstract harmonic analysis, D. Van Nostrand, pp. x+190, hdl:2027/uc1.b4250788  
• en Mac Lane, Saunders (1998), Categories for the Working Mathematician (ed. 2nd), Springer-Verlag, ISBN 978-0-387-98403-2 
• en Mazur, Barry (1973), „Notes on étale cohomology of number fields”, Annales Scientifiques de l'École Normale Supérieure, Série 4, 6 (4): 521–552, doi:10.24033/asens.1257 , ISSN 0012-9593, MR 0344254 
• en Milne, James S. (1980), Étale cohomology, Princeton University Press, ISBN 978-0-691-08238-7 
• en Milne, James S. (2006), Arithmetic duality theorems (ed. 2nd), Charleston, South Carolina: BookSurge, LLC, ISBN 978-1-4196-4274-6, MR 2261462 
• en Negrepontis, Joan W. (1971), „Duality in analysis from the point of view of triples”, Journal of Algebra, 19 (2): 228–253, doi:10.1016/0021-8693(71)90105-0 , ISSN 0021-8693, MR 0280571 
• en Veblen, Oswald; Young, John Wesley (1965), Projective geometry. Vols. 1, 2, Blaisdell Publishing Co. Ginn and Co., MR 0179666 
• en Weibel, Charles A. (1994), An introduction to homological algebra, Cambridge University Press, ISBN 978-0-521-55987-4, MR 1269324 
• en Edwards, R. E. (1965). Functional analysis. Theory and applications. New York: Holt, Rinehart and Winston. ISBN 0030505356. 

Portal Matematică