Fagure tetraedric-octaedric

Fagure tetraedric-octaedric
Nume alternativ: Fagure cubic alternat
Tip	Fagure uniform, simplectic
Simbol Schläfli	h{4,3,4} {3^[4]} ht0,3{4,3,4} h{4,4}h{∞} ht0,2{4,4}h{∞} h{∞}h{∞}h{∞} s{∞}s{∞}s{∞}
Diagramă Coxeter	= = = =
Celule	{3,3} {3,4}
Fețe	triunghi {3}
Laturi	[{3,3}.{3,4}]^2 (dreptunghi)
Figura vârfului	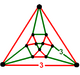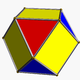(cuboctaedru)
Grup Coxeter	${\displaystyle {\tilde {B}}_{3}}$, [4,3^1,1]
Grup de simetrie	Fm3m (225)
Dual	Fagure dodecaedric rombic
Proprietăți	Fagure cvasiregulat, convex, tranzitiv pe vârfuri și laturi
Index uniform	J21,31,51, A2, W9, G1[1]

Un fagure tetraedric-octaedric sau fagure cubic alternat este o teselare cvasiregulată (sau fagure) a spațiului euclidian tridimensional. Este format din octaedre și tetraedre regulate, în raport de 1:2. Este tranzitiv pe vârfuri, având câte 8 tetraedre și 6 octaedre în jurul fiecărui vârf. Este și tranzitiv pe laturi, cu căte 2 tetraedre și 2 octaedre care se întâlnesc alternativ pe fiecare latură. Dualul său este fagurele dodecaedric rombic.

Face parte dintr-o familie infinită de faguri uniformi numiți faguri hipercubici alternați, format ca o alternare a unui fagure hipercubic. De asemenea, face parte dintr-o altă familie infinită de faguri uniformi, numiți faguri simplectici.

În acest caz din spațiul tridimensional, fagurele cubic este alternat, reducând celulele cubice la tetraedre, iar vârfurile eliminate lasă goluri octaedrice. Ca atare, poate fi reprezentat printr-un simbol Schläfli h{4,3,4} extins, conținând jumătate din vârfurile fagurelui cubic {4,3,4}.

Există un fagure similar, numit fagure tetraedric-octaedric girat care are straturile rotite la 60°, astfel încât în jumătate din laturi se învecinează tetraedre cu tetraedre și octaedre cu octaedre în loc de tetraedre cu octaedre, ca urmare acesta nu este tranzitiv pe laturi.

Fagurele tetraedric-octaedric poate avea simetria dublată prin plasarea tetraedrelor pe celulele octaedrice, creând un fagure neuniform format din tetraedre și octaedre (ca antiprisme triunghiulare). Figura vârfului său este un tetraedru triakis trunchiat de ordinul 3. Acest fagure este dualul fagurelui tetraedric triakis trunchiat, format din celule tetraedrice triakis trunchiate.

Coordonate carteziene

La un fagure cubic alternat, cu laturile paralele cu axele și cu lungimea laturii 1, pentru toate valorile întregi: ${\displaystyle i,j,k}$ cu ${\displaystyle i+j+k}$ par, coordonatele carteziene ale vârfurilor sunt:

${\displaystyle (i,j,k)}$

Vedere expandată a celulelor din jurul unui vârf

Simetrie

Există două construcții prin reflexii și multe prin alternarea fagurelui cubic; exemple:

Simetrie	${\displaystyle {\tilde {B}}_{3}}$, [4,3^1,1] = ½${\displaystyle {\tilde {C}}_{3}}$, [1^+,4,3,4]	${\displaystyle {\tilde {A}}_{3}}$, [3^[4]] = ½${\displaystyle {\tilde {B}}_{3}}$, [1^+,4,3^1,1]	[[(4,3,4,2^+)]]	[(4,3,4,2^+)]
Grup spațial^⁠(d)	Fm3m (225)	F43m (216)	I43m (217)	P43m (215)
Imagine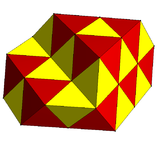
Tipuri de tetraedre	1	2	3	4
Diagramă Coxeter	=	= =

Straturi alternate la fagurele cubic

Fagurele cubic alternat poate fi divizat în straturi, unde sunt create noi fețe pătrate în interiorul octaedrelor. Fiecare strat va conține piramide pătrate orientate în sus și în jos și tetraedre așezate pe laturile lor. O a doua direcție de divizare nu necesită fețe noi și prezintă tetraedre și octaedre dispuse alternativ. Acest fagure din plăci este mai degrabă un fagure scaliform decât unul uniform, deoarece are celule neuniforme.

Proiecții prin pliere

Grup Coxeter	${\displaystyle {\tilde {A}}_{3}}$	${\displaystyle {\tilde {C}}_{2}}$
Diagramă Coxeter
Imagine
Nume	fagure cubic alternat	pavare pătrată

Fagurele cubic alternat poate fi proiectat ortogonal în pavarea pătrată plană printr-o operație de pliere geometrică care aplică o pereche de oglinzi una pe alta. Proiecția fagurelui cubic alternat creează două copii decalate ale aranjamentului vârfurilor planului:

Rețeaua A3/D3

Aranjamentul vârfurilor sale reprezintă o rețea A₃^⁠(d).^[2][3] Această rețea este cunoscută în cristalografie ca rețeaua cubică cu fețe centrate, în care vârfurile sunt centrele unei împachetări strânse de sfere egale, care atinge cea mai mare densitate medie posibilă. Fagurele tetraedric-octaedric este cazul tridimensional al unui fagure simplectic. Celula sa Voronoi^⁠(d) este un dodecaedru rombic, dualul figurii vârfului cuboctaedrului pentru fagurele tetraedric-octaedric.

Împachetarea D+
3 poate fi construită prin reuniunea a două rețele D₃ (sau A₃). Împachetarea D+
n este o rețea doar pentru dimensiuni pare. Numărul punctelor de contact este 2²=4, (2ⁿ⁻¹ pentru n < 8, 240 pentru n=8 și 2n(n−1) pentru n > 8).^[4]

∪

Rețeaua A*
3 sau rețeaua D*
3 (numite și A4
3 și D4
3) pot fi construite din reuniunea a patru rețele A₃ și este identică cu aranjamentul vârfurilor fagurelui bisfenoid tetragonal^⁠(d), fagure dual al fagurelui cubic bitrunchiat.^[5] Este și rețeaua cubică centrată intern, reuniunea a doi faguri cubici aflați în poziții duale.

∪ ∪ ∪ = dual al = ∪ .

Numărul punctelor de contact al rețelei D*
3 este 8^[6] iar teselarea sa Voronoi este fagurele cubic bitrunchiat, , care conține toate celulele Voronoi octaedrice trunchiate, .^[7]

Note

1. en For cross-referencing, they are given with list indices from Andreini (1-22), Williams(1-2,9-19), Johnson (11-19, 21-25, 31-34, 41-49, 51-52, 61-65), and Grünbaum(1-28).
2. en „The Lattice D3”. 
3. en „The Lattice A3”. 
4. Conway (1998), p. 119
5. en „The Lattice D3”. 
6. Conway (1998), p. 120
7. Conway (1998), p. 466

Bibliografie

• en John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN: 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292–298, includes all the nonprismatic forms)
• en George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
• en Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
• en Norman Johnson Uniform Polytopes, Manuscript (1991)
• en Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. 
• en Critchlow, Keith (1970). Order in Space: A design source book. Viking Press. ISBN 0-500-34033-1. 
• en Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN: 978-0-471-01003-6 [1]

• (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10] (1.9 Uniform space-fillings)
• (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]

• it Alfredo Andreini, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative, Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
• en Duncan MacLaren Young Sommerville, An Introduction to the Geometry of n Dimensions. New York, E. P. Dutton, 1930. 196 pp. (Dover Publications edition, 1958) Chapter X: The Regular Polytopes
• en Conway JH, Sloane NJH (1998). Sphere Packings, Lattices and Groups (ed. 3rd). ISBN 0-387-98585-9. 

Legături externe

• Materiale media legate de fagure tetraedric-octaedric la Wikimedia Commons
• en Architectural design made with Tetrahedrons and regular Pyramids based square.(2003) Arhivat în 4 martie 2016, la Wayback Machine.
• en Klitzing, Richard. „3D Euclidean Honeycombs x3o3o *b4o - octet - O21”. 
• en Uniform Honeycombs in 3-Space: 11-Octet

Portal Matematică

v • d • m Faguri convecși regulați și uniformi în dimensiunile 2–8
Spațiu	Familia	${\displaystyle {\tilde {A}}_{n-1}}$	${\displaystyle {\tilde {C}}_{n-1}}$	${\displaystyle {\tilde {B}}_{n-1}}$	${\displaystyle {\tilde {D}}_{n-1}}$	${\displaystyle {\tilde {G}}_{2}}$ / ${\displaystyle {\tilde {F}}_{4}}$ / ${\displaystyle {\tilde {E}}_{n-1}}$
E^2	Pavare uniformă	{3^[3]}	δ3	hδ3	qδ3	Hexagonală
E^3	Fagure convex uniform	{3^[4]}	δ4	hδ4	qδ4
E^4	4-fagure uniform	{3^[5]}	δ5	hδ5	qδ5	Fagure 24-celule
E^5	5-fagure uniform	{3^[6]}	δ6	hδ6	qδ6
E^6	6-fagure uniform	{3^[7]}	δ7	hδ7	qδ7	222
E^7	7-fagure uniform	{3^[8]}	δ8	hδ8	qδ8	133 • 331
E^8	8-fagure uniform	{3^[9]}	δ9	hδ9	qδ9	152 • 251 • 521
E^n-1	(n−1)-fagure uniform	{3^[n]}	δn	hδn	qδn	1k2 • 2k1 • k21