Hemipoliedru
În geometrie un hemipoliedru este un poliedru stelat uniform ale cărui fețe trec prin centrul său. Aceste fețe hemi sunt paralele cu fețele unui alt poliedru simetric, iar numărul lor este jumătate din numărul de fețe ale celuilalt poliedru, de unde prefixul „hemi”.[1]
Prefixul „hemi” este folosit și pentru a se referi la anumite poliedre proiective, cum ar fi hemicubul, care sunt imaginea unei aplicări 2 pe 1 a unui poliedru sferic cu simetrie față de centru.
Simbol Wythoff și figura vârfului
[modificare | modificare sursă]Simbolurile lor Wythoff sunt de forma p/(p − q) p/q | r. Figurile vârfurilor lor sunt patrulatere. Ele sunt astfel legate de poliedrele cantelate, care au simboluri Wythoff similare. Configurația vârfului este p/q.2r.p/(p − q).2r. Fețele 2r-gonale trec prin centrul poliedrului: dacă sunt reprezentate ca fețe ale unor poliedre sferice, ele acoperă o întreagă emisferă, iar laturile și vârfurile lor se află pe un cerc mare. Notația p/(p − q) implică {p/q} fața întorcându-se înapoi în jurul figurii vârfului.
Cele nouă forme, împreună cu simbolurile lor Wythoff și configurațiile vârfurilor lor sunt:
 Tetrahemihexaedru 3/2 3 | 2 (3.4.3/2.4) (p/q = 3, r = 2) |
 Octahemioctaedru 3/2 3 | 3 (3.6.3/2.6) (p/q = 3, r = 3) |
 Micul icosihemidodecaedru 3/2 3 | 5 (3.10.3/2.10) (p/q = 3, r = 5) |
 Marele icosihemidodecaedru 3/2 3 | 5/3 (3.10/3.3/2.10/3) (p/q = 3, r = 5/3) |
 Micul dodecahemicosaedru 5/3 5/2 | 3 (5/2.6.5/3.6) (p/q = 5/2, r = 3) |
 Cubohemioctaedru 4/3 4 | 3 (4.6.4/3.6) (p/q = 4, r = 3) |
 Micul dodecahemidodecaedru 5/4 5 | 5 (5.10.5/4.10) (p/q = 5, r = 5) |
 Marele dodecahemidodecaedru 5/3 5/2 | 5/3 (5/2.10/3.5/3.10/3) (p/q = 5/2, r = 5/3) |
 Marele dodecahemicosaedru 5/4 5 | 3 (5.6.5/4.6) (p/q = 5, r = 3) |
De observat că construcția caleidoscopică a lui Wythoff generează hemipoliedrele neorientabile (toate cu excepția octahemioctaedrului) ca acoperiri duble (două hemipoliedre care coincid).
În planul euclidian șirul de hemipoliedre continuă cu următoarele patru pavări stelate, unde apeirogoanele apar ca poligoane ecuatoriale menționate mai sus:
| Pavarea rectificată originală |
Imaginea laturilor |
Umplerea | Configurația vârfurilor |
Simbol Wythoff |
Simetrie |
|---|---|---|---|---|---|
 Pavare pătrată |
 |
 |
4.∞.4/3.∞ 4.∞.-4.∞ |
4/3 4 | ∞ | p4m |
 Pavare triunghiulară |
 |
 |
(3.∞.3.∞.3.∞)/2 | 3/2 | 3 ∞ | p6m |
 Pavare trihexagonală |
 |
 |
6.∞.6/5.∞ 6.∞.-6.∞ |
6/5 6 | ∞ | |
 |
∞.3.∞.3/2 ∞.3.∞.-3 |
3/2 3 | ∞ |
Dintre aceste patru pavări, doar 6/5 6 | ∞ este generată prin construcția Wythoff ca o acoperire dublă.
Orientabilitate
[modificare | modificare sursă]Doar octahemioctaedrul are o suprafață orientabilă, celelalte hemipoliedre au suprafețe neorientabile sau cu o singură față.
Duale ale hemipoliedrelor
[modificare | modificare sursă]Deoarece hemipoliedrele au fețe care trec prin centru, dualele lor au vârfurile corespunzătoare la infinit, propriu-zis pe planul proiectiv real(d) la infinit.[2] În Dual Models de Magnus Wenninger, ele sunt reprezentate ca prisme care se intersectează, fiecare extinzându-se în ambele direcții până la același vârf de la infinit, pentru a menține simetria. În practică, prismele modelului sunt retezate la un anumit punct, convenabil pentru producător. Wenninger a sugerat că aceste figuri sunt membre ale unei noi clase de figuri stelate, numite stelări la infinit. El a mai sugerat că, strict vorbind, ele nu sunt poliedre, deoarece construcția lor nu este conformă definițiilor uzuale.
Există 9 astfel de duale, cu doar 5 forme exterioare distincte, patru dintre ele existente în perechi identice la exterior. Membrii unei perechi identice din punct de vedere vizual diferă prin aranjamentele vârfurilor lor adevărate și false (un vârf fals este locul în care două laturi se intersectează, dar nu se unesc). Formele exterioare sunt:

|

|

|

|

|
| Tetrahemihexacron | Octahemioctacron și hexahemioctacron |
Micul icosihemidodecacron și micul dodecahemidodecacron |
Marele dodecahemidodecacron și marele icosihemidodecacron |
Marele dodecahemicosacron și micul dodecahemicosacron |
| 3 prisme pătrate infinite care se intersectează | 4 prisme hexagonale infinite care se intersectează | 6 prisme decagonale infinite care se intersectează | 6 prisme decagramice infinite care se intersectează | 10 prisme hexagonale infinite care se intersectează |
Relația cu poliedrele cvasiregulate
[modificare | modificare sursă]Hemipoliedrele apar în perechi ca fațetări ale poliedrelor cvasiregulate cu patru fețe la un vârf. Aceste poliedre cvasiregulate au configurațiile vârfurilor m.n.m.n, iar laturile lor, pe lângă faptul că formează fețe m- și n-gonale, formează și hemifețe ale hemipoliedrelor. Astfel, hemipoliedrele pot fi derivate din poliedre cvasiregulate prin eliminarea fie a m-goanelor, fie a n-goanelor (pentru a menține două fețe la o latură) și apoi inserând hemifețele. Deoarece fie m-goanele, fie n-goanele pot fi eliminate, oricare dintre cele două hemipoliedre pot fi derivate din fiecare poliedru cvasiregulat, cu excepția octaedrului ca tetratetraedru, unde m = n = 3, iar cele două fațete sunt congruente. (Această construcție nu funcționează pentru poliedre cvasiregulate cu șase fețe la un vârf, cunoscute și sub denumirea de poliedre ditrigonale, deoarece laturile lor nu formează hemifețe regulate.)[1]
Deoarece hemipoliedrele, ca și poliedrele cvasiregulate, au câte două tipuri de fețe care alternează în jurul fiecărui vârf, ele sunt uneori considerate a fi cvasiregulate.[1]
| Poliedru cvasiregulat m.n.m.n |
Hemifețe (h-goane |
Hemipoliedru cu m-goane eliminate n.h.n/n−1.h |
Hemipoliedru cu n-goane eliminate m.h.m/m−1.h |
|---|---|---|---|
 Tetratetraedru 3.3.3.3 m = 3, n = 3 |
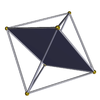 pătrate {4} |
 Tetrahemihexaedru 3.4.3/2.4 |
 Tetrahemihexaedru 3.4.3/2.4 |
 Cuboctaedru 3.4.3.4 m = 3, n = 4 |
 hexagoane {6} |
 Cubohemioctaedru 4.6.4/3.6 |
 Octahemioctaedru 3.6.3/2.6 |
 Icosidodecaedru 3.5.3.5 m = 3, n = 5 |
 decagoane {10} |
 Micul dodecahemidodecaedru 5.10.5/4.10 |
 Micul icosihemidodecaedru 3.10.3/2.10 |
 Dodecadodecaedru 5.5/2.5.5/2 m = 5, n = 5/2 |
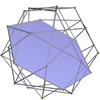 hexagoane {6} |
 Micul dodecahemicosaedru 5/2.6.5/3.6 |
 Marele dodecahemicosaedru 5.6.5/4.6 |
 Marele icosidodecaedru 3.5/2.3.5/2 m = 3, n = 5/2 |
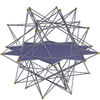 decagrame {10/3} |
 Marele dodecahemidodecaedru 5/2.10/3.5/3.10/3 |
 Marele icosihemidodecaedru 3.10/3.3/2.10/3 |
Aici m și n corespund cu p/q de mai sus, iar h corespunde cu 2r de mai sus.
Note
[modificare | modificare sursă]- ^ a b c en Hart, George (). „Quasiregular Polyhedra”. Virtual Polyhedra: The Encyclopedia of Polyhedra. Accesat în .
- ^ en (Wenninger 2003, p. 101)
Bibliografie
[modificare | modificare sursă]- en Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (), „Uniform polyhedra”, Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, The Royal Society, 246 (916): 401–450, doi:10.1098/rsta.1954.0003, ISSN 0080-4614, JSTOR 91532, MR 0062446
- en Wenninger, Magnus (), Polyhedron Models, Cambridge University Press, ISBN 978-0-521-09859-5, MR 0467493 (Wenninger models: 67, 68, 78, 89, 91, 100, 102, 106, 107)
- en Wenninger, Magnus (), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 0730208
- en Har'El, Z. Uniform Solution for Uniform Polyhedra. Arhivat în , la Wayback Machine., Geometriae Dedicata 47, 57-110, 1993. Zvi Har’El Arhivat în , la Wayback Machine. (Page 10, 5.2. Hemi polyhedra p p'|r.)
Legături externe
[modificare | modificare sursă]- en Stella Polyhedral Glossary
- en Versi-Regular Polyhedra in Visual Polyhedra
| |||||||||||||||||||||||||||


