Pavare triunghiulară de ordinul 7

Pavare triunghiulară
de ordinul 7
Pe modelul discului Poincaré al planului hiperbolic
Descriere
Tippavare hiperbolică
Configurația vârfului3.3.3.3.3.3.3 (sau 37)
Configurația fețeiV7.7.7 (sau V73)
Simbol Wythoff7 | 3 2
Simbol Schläfli{3,7}
Diagramă Coxeter
Grup de rotație[7,3]+, (732)
Poliedru dualpavare heptagonală de ordinul 3
Figura vârfului
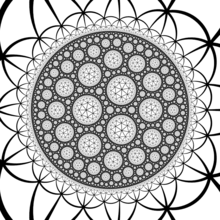
Fagurele {3,3,7} are figura vârfului {3,7}

În geometrie pavarea triunghiulară de ordinul 7 este o pavare hiperbolică regulată a planului hiperbolic cu simbolul Schläfli {3,7}, având șapte triunghiuri regulate în jurul fiecărui vârf.

Suprafețe Hurwitz

[modificare | modificare sursă]

Grupul de simetrie al pavării este Grupul triunghiului (2,3,7), iar domeniul său fundamental este triunghiul Schwarz (2,3,7). Acesta este cel mai mic triunghi Schwarz hiperbolic și, prin urmare, prin demonstrarea teoremei lui Hurwitz despre automorfisme, pavarea triunghiulară de ordinul 7 este pavarea universală care acoperă toate suprafețele Hurwitz (suprafețele Riemann cu grup de simetrie maxim), formând o triangulare al cărei grup de simetrie este egal cu grupul lor de automorfism ca suprafețe Riemann.

Cea mai mică dintre acestea este cvartica Klein⁠(d), cea mai simetrică suprafață de genul 3, împreună cu o pavare cu 56 de triunghiuri, întâlnindu-se în 24 de vârfuri, cu grupul de simetrie grupul simplu de ordinul 168, cunoscut sub numele de PSL(2,7). Suprafața rezultată poate fi, la rândul său, imersată⁠(d) poliedric în spațiul euclidian tridimensional, rezultând micul cubicuboctaedru.[1]

Duala sa, pavarea heptagonală de ordinul 3, are același grup de simetrie, generând astfel pavări heptagonale ale suprafețelor Hurwitz.


Grupul de simetrie al pavării triunghiulare de ordinul 7 are domeniul fundamental triunghiul Schwarz (2,3,7), care duce la aceasta
Micul cubicuboctaedru este o imersiune poliedrică a cvarticei Klein,[1] care, ca toate suprafețele Hurwitz, este un spațiu cât al acestei pavări

Poliedre și pavări înrudite

[modificare | modificare sursă]

Este înrudită cu două pavări stelate prin același aranjament al vârfurilor: pavare heptagramică de ordinul 7, {7/2,7} și pavarea heptagonală de ordin heptagramic, {7,7/2}.

Este legată topologic ca parte a secvenței de poliedre regulate cu simbolul Schläfli {3,p}.

Variante de pavări regulate cu simetrie: *n32
Sferice Euclid. Hiperb. compacte Paraco. Hiperbolice necompacte
3.3 33 34 35 36 37 38 3∞ 312i 39i 36i 33i

Este parte a seriei regulate {n,7}:

Pavări de forma {n,7}
Sferică Pavări hiperbolice

{2,7}
{3,7}
{4,7}
{5,7}
{6,7}
{7,7}
{8,7}
 ...
{∞,7}

Dintr-o construcție Wythoff se obțin opt pavări uniforme ale planului hiperbolic, care pot fi bazate pe pavarea heptagonală regulată și pavarea triunghiulară de ordinul 7.

Desenând dalele colorate în roșu pe fețele originale, galben la vârfurile originale și albastru de-a lungul laturilor, există 8 forme.

Pavări heptagonale/triunghiulare uniforme    
v • d • m
Simetrie: [7,3], (*732) [7,3]+, (732)
{7,3} t{7,3} r{7,3} t{3,7} {3,7} rr{7,3} tr{7,3} sr{7,3}
Dualele celor de mai sus
V73 V3.14.14 V3.7.3.7 V6.6.7 V37 V3.4.7.4 V4.6.14 V3.3.3.3.7


Note

[modificare | modificare sursă]
  1. ^ a b en (Richter) Fiecare față din poliedru este formată din mai multe fețe în pavare — două fețe triunghiulare formează o față pătrată, v. această imagine Arhivat în , la Wayback Machine.

Bibliografie

[modificare | modificare sursă]
  • en John Horton Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN: 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
  • en „Chapter 10: Regular honeycombs in hyperbolic space”. The Beauty of Geometry: Twelve Essays. Dover Publications. . ISBN 0-486-40919-8. LCCN 99035678. 
  • en Richter, David A., How to Make the Mathieu Group M24, arhivat din original la , accesat în  

Legături externe

[modificare | modificare sursă]
Portal icon Portal Matematică