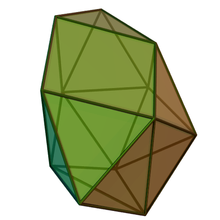
Sfenomegacoroană

Sfenomegacoroană
(model 3D)
Descriere
Tip	poliedru Johnson J87 – J88 – J89
Fețe	18 (16 triunghiuri echilaterale,         2 pătrate)[1]
Laturi (muchii)	28[1]
Vârfuri	12[1]
χ	2
Configurația vârfului	2 (3^4); 2 (3^2.4^2); 4 (3^5); 4 (3^4.4)
Grup de simetrie	C2v , [2], [*22], ordin 4
Arie	≈ 8,928 a^2   (a = latura)
Volum	≈ 1,948 a^3   (a = latura)
Poliedru dual	–
Proprietăți	Convex
Desfășurată

În geometrie sfenomegacoroana este unul dintre poliedrele Johnson, (J₈₈).^[1][2] Este unul dintre poliedrele elementare Johnson care nu se pot obține prin „tăiere și lipire” ale poliedrelor platonice sau arhimedice. Având 18 fețe, este un octadecaedru.

Construcție

Este construit prin adăugarea unei piramide pătrate, (J₁), pe una din fețele pătrate ale unei sfenocoroane, (J₈₆). Este singurul poliedru Johnson care este obținut prin operații de „tăiere și lipire” în care componentele nu sunt toate prisme, antiprisme sau părți de poliedre platonice sau arhimedice.

Johnson folosește prefixul sfeno- pentru a se referi la un complex asemănător unei pene format din două lunule adiacente (o lunulă fiind un pătrat cu triunghiuri echilaterale atașate pe laturile opuse). De asemenea, sufixul -megacoroană se referă la un complex în formă de coroană format din 12 triunghiuri, în contrast cu complexul mai mic, format din 8 triunghiuri, din sfenocoroană. Unirea ambelor complexe produce sfenomegacoroana.^[2]

Mărimi asociate

Coordonate carteziene

Pentru a calcula coordonatele carteziene pentru sfenomegacoronă, fie k ≈ 0,59463 cea mai mică rădăcină pozitivă a polinomului de gradul 16

${\displaystyle {\begin{aligned}&1680~x^{16}-4800~x^{15}-3712~x^{14}+17216~x^{13}\\&\quad +1568~x^{12}-24576~x^{11}+2464~x^{10}+17248~x^{9}\\&\quad -3384~x^{8}-5584~x^{7}+2000~x^{6}+240~x^{5}\\&\quad -776~x^{4}+304~x^{3}+200~x^{2}-56~x-23.\end{aligned}}}$

Atunci, coordonatele carteziene ale unei sfenomegacoroane cu lungimea laturilor 2 sunt date de reuniunea orbitelor punctelor

${\displaystyle {\begin{aligned}&\left(0,1,2{\sqrt {1-k^{2}}}\right),\,(2k,1,0),\,\left(0,{\frac {\sqrt {3-4k^{2}}}{\sqrt {1-k^{2}}}}+1,{\frac {1-2k^{2}}{\sqrt {1-k^{2}}}}\right),\\&\left(1,0,-{\sqrt {2+4k-4k^{2}}}\right),\,\left(0,{\frac {{\sqrt {3-4k^{2}}}\left(2k^{2}-1\right)}{\left(k^{2}-1\right){\sqrt {1-k^{2}}}}}+1,{\frac {2k^{4}-1}{\left(1-k^{2}\right)^{\frac {3}{2}}}}\right)\end{aligned}}}$

sub acțiunea grupului generat de reflexiile față de planele xz și yz.^[3]

Arie și volum

Următoarele formule pentru arie, A^[1] și volum, V sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:

${\displaystyle A=2(1+2{\sqrt {3}})\,a^{2}\approx 8,928203~a^{2},}$

Pentru volum se calculează ${\displaystyle \xi }$ ca rădăcina minimă pozitivă a polinomului de gradul 32:^[4]

   521578814501447328359509917696 x³²

− 985204427391622731345740955648 x³⁰

− 16645447351681991898880656015360 x²⁸

+ 79710816694053483249372512649216 x²⁶

− 152195045391070538203422101864448 x²⁴

+ 156280253448056209478031589244928 x²²

− 96188116617075838858708654227456 x²⁰

+ 30636368373570166303441645731840 x¹⁸

+ 5828527077458909552923002273792 x¹⁶

− 8060049780765551057159394951168 x¹⁴

+ 1018074792115156107372011716608 x¹²

+ 35220131544370794950945931264 x¹⁰

+ 327511698517355918956755959808 x⁸

− 116978732884218191486738706432 x⁶

+ 10231563774949176791703149568 x⁴

− 366323949299263261553952192 x²

+ 3071435678740442112675625 ,

cu care volumul este:

${\displaystyle V=\xi \,a^{3}\approx 1,948108~a^{3}.}$

Note

1. ^ en Stephen Wolfram, "Sphenomegacorona" from Wolfram Alpha. Retrieved March 4, 2023.
2. ^ en Johnson, Norman W. (1966), „Convex polyhedra with regular faces”, Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603 
3. en Timofeenko, A. V. (2009). „The non-Platonic and non-Archimedean noncomposite polyhedra”. Journal of Mathematical Science. 162 (5): 718. doi:10.1007/s10958-009-9655-0. 
4. Șirul A334114 la Enciclopedia electronică a șirurilor de numere întregi (OEIS)

Legături externe

Portal Matematică

• en Eric W. Weisstein, Sphenomegacorona la MathWorld.
• en Eric W. Weisstein, Johnson solid la MathWorld.