R-дерево Гильберта

R-дерево Гильберта, вариант R-дерева — это индексация многомерных объектов, таких как прямые, двумерные области, трёхмерные объекты или снабжённые параметрами объекты более высоких размерностей. Их можно понимать как расширение B+-деревьев на многомерные объекты.

Производительность R-деревьев зависит от качества алгоритма, группирующего данные в прямоугольники. R-деревья используют заполняющие пространство кривые, точнее, кривые Гильберта, для линейного упорядочивания объектов в прямоугольники.

Существует два типа R-деревьев Гильберта, одно для статических данных, другое для динамических. В обоих случаях для получения лучшего упорядочения многомерных объектов используются заполняющие пространство кривые Гильберта. Это упорядочение «хорошее» в смысле, что оно должно бы группировать «похожие» данные в прямоугольники, минимизируя площадь и периметр этих минимальных ограничительных прямоугольников^[англ.] (Minimum Bounding Rectangle, MBR). Упакованные R-деревья Гильберта пригодны для статических данных, обновляемых очень редко или не обновляемых вообще.

Динамичные R-деревья Гильберта пригодны для изменяемых данных, где вставки, удаления или обновления происходят в режиме реального времени. Более того, динамичные R-деревья Гильберта используют гибкий отложенный механизм расщепления, что улучшает обработку пространства. Каждый узел имеет чётко определённое множество родственных (с одним родителем) узлов. Регулируя политику расщепления, с помощью R-деревьев Гильберта можно получить степень обработки пространства на желаемом уровне. R-деревья Гильберта сортируют прямоугольники согласно гильбертовым расстояниям центров прямоугольников (MBR). (Гильбертово расстояние точки равно длине кривой Гильберта от начала кривой до точки.). В противоположность этому другие варианты R-деревьев не имеют механизмов контроля над обработкой пространства.

Основная идея

Хотя следующий пример относится к статическому окружению, он объясняет интуитивные принципы построения хороших R-деревьев. Эти принципы верны как для статических, так и для динамических данных. Руссопулос и Ляйфкер предложили метод построения упакованного R-дерева, которое позволяет достичь обработки почти 100 % пространства. Идея заключается в сортировке данных по координате x или y от одного угла прямоугольника. Сортировки по любому из четырёх углов дают похожие результаты. В данной статье точки и прямоугольники сортируются относительно координаты x левого нижнего угла прямоугольника, а метод Руссопулоса и Ляйфкера будем называть «упакованным по x R-деревом». Метод просматривает сортированный список прямоугольников. Последовательные прямоугольники назначаются тому же листу R-дерева, пока узел не заполнится. Затем создаётся новый лист и просмотр сортированного списка продолжается. Таким образом, узлы получаемого R-дерева будут полностью упакованы, за возможным исключением последнего узла на каждом уровне. Таким образом, обработка пространства близка к 100 %. Более высокие уровни дерева создаются аналогично.

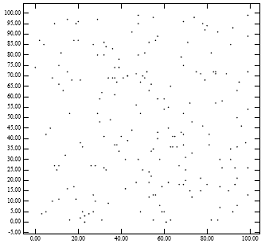
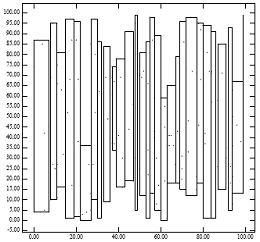
Рисунок 1 показывает проблемы упакованных по x R-деревьев. На рисунке (справа) показаны узлы R-дерева, полученные этим методом для точек, показанных слева. Факт, что получаемые родительские узлы покрывают малое пространство, объясняет быструю деградацию запросов для точек. Большой периметр прямоугольников объясняет, однако, почему происходит быстрая деградация запросов для областей. Это согласуется с аналитическими формулами производительности R-деревьев^[1]. Интуитивно ясно, что алгоритм упаковки должен бы назначать близкие точки тому же самому узлу. Игнорирование координаты y «упакованным по x R-деревом» приводит к нарушению этого эмпирического правила.

Рисунок 1: [Слева] 200 равномерно распределённых точек. [Справа] MBR узлов, образованных алгоритмом «упаковки по x R-дерева»

Кривая Гильберта

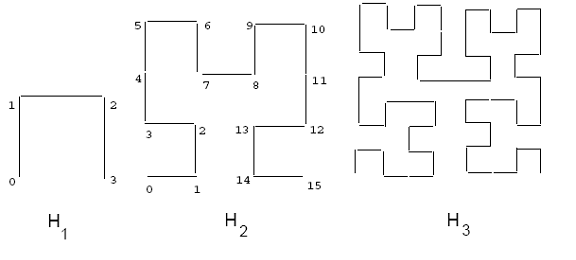
Начальная кривая Гильберта на решётке 2x2, имеющая обозначение H₁, показана на рисунке 2. Чтобы получить кривую порядка i, каждая вершина основной кривой заменяется на кривую порядка i – 1, нужным образом повёрнутой и/или отражённой. На рисунке 2 показаны также кривые Гильберта порядка два и три. При стремлении порядка кривой к бесконечности, подобно другим заполняющим пространство кривым, кривая превращается во фрактал с фрактальной размерностью два^[1][2]. Кривую Гильберта можно обобщить на более высокие размерности. Алгоритм рисования двумерной кривой заданного порядка можно найти у Гриффитса^[3] и Джагадиша^[2]. Алгоритм для более высоких размерностей дал Байалли^[4].

Заполняющая пространство кривая создаёт линейное упорядочение точек решётки. Этот путь может быть построен, начав от одного конца кривой до другого, пройдя все точки до конца кривой. Фигура 2 показывает одно такое упорядочение для решётки 4x4 (см. кривую H₂). Например, точка (0,0) на кривой H₂ имеет расстояние 0, а точка (1,1) имеет расстояние 2. Гильбертово расстояние прямоугольника равно по определению гильбертову расстоянию его центра.

Рисунок 2: Кривые Гильберта порядка 1, 2 и 3

Упакованные R-деревья Гильберта

Кривая Гильберта задаёт линейное упорядочение на прямоугольниках данных. Проходя по упорядоченному списку, назначаем каждое множество прямоугольников узлу R-дерева. В результате множество прямоугольников данных на том же узле будут близки друг другу в линейном порядке и, наиболее вероятно, близки в естественном пространстве. Таким образом, полученные узлы R-дерева будут иметь малую площадь. Рисунок 2 показывает причины, почему методы, основанные на кривых Гильберта, приводят к хорошей производительности. Данные состоят из точек (тех же, что и на рисунке 1). Группируя точки согласно их гильбертовым расстояниям, MBR результирующих узлов R-дерева обычно являются маленькими близкими к квадратам прямоугольниками. Это означает, что узлы с большой вероятностью будут иметь малые площади и периметры. Малые значения площадей приводит к хорошей производительности запросов для точек. Малые площади и малые значения периметров приводят к хорошей производительности для больших запросов.

Алгоритм упаковки «Hilbert-Pack»

(Алгоритм упаковки прямоугольников в R-дерево)
Шаг 1. Вычисляем гильбертово расстояние для каждого прямоугольника данных
Шаг 2. Сортируем прямоугольники по возрастанию гильбертова расстояния
Шаг 3. /* Создаём листья (уровень l=0) */

• Пока (имеются ещё прямоугольники)
  • образуем новый узел R-дерева
  • назначаем следующий прямоугольник C этому узлу

Шаг 4. /* Создаём узлы на уровне (l + 1) */

• Пока (существует > 1 узлов на уровне l)
  • сортируем узлы на уровне l ≥ 0 по возрастанию времени создания
  • повторяем Шаг 3

Здесь предполагается, что данные статические или меняются нечасто. Алгоритм является простым эвристическим алгоритмом для построения R-дерева со 100 % обработкой пространства, имеющим к тому же хорошее время ответа.

Динамические R-деревья Гильберта

Производительность R-деревьев зависит от качества алгоритма кластеризации данных в прямоугольники в узле. R-деревья Гильберта используют заполняющие пространство кривые с линейным упорядочением прямоугольников. Гильбертово расстояние прямоугольника по определению равно расстоянию его центра.

Структура дерева

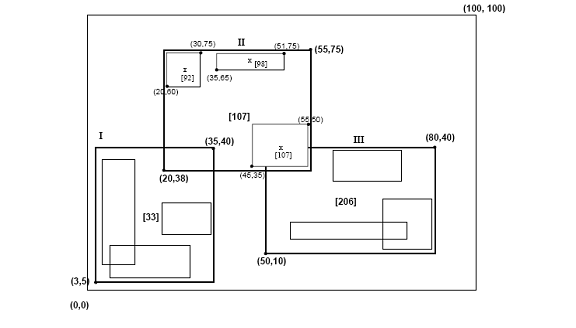
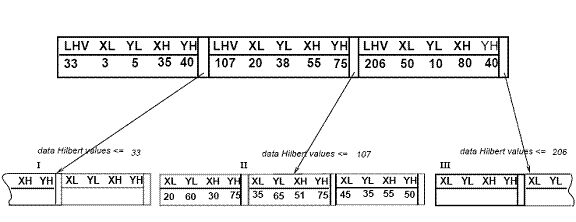
R-дерево Гильберта имеет следующую структуру. Лист содержит максимум C_l элементов, каждый из которых имеет вид (R, obj _id), где C_l — ёмкость листа, R — MBR реального объекта (x_low, x_high, y_low, y_high), а obj-id — указатель на запись описания объекта. Главное отличие между R-деревом Гильберта и R*-деревом ^[5] заключается в том, что узлы, не являющиеся листами, содержат информацию о LHV (Largest Hilbert Value, Наибольшее Гильбертово Расстояние). Таким образом узлы, не являющиеся листами, в R-дереве содержат максимум C_n элементов вида (R, ptr, LHV), где C_n — ёмкость узла, не являющегося листом, R — MBR, включающее всех потомков этого узла, ptr — указатель на потомка, и LHV является наибольшим гильбертовым расстоянием данных в ограничивающем прямоугольнике R. Заметим, что поскольку узел, не являющийся листом, имеет в качестве своего LHV гильбертово расстояние одного из своих потомков, нет дополнительной цены для вычисления гильбертовых расстояний MBR узлов, не являющихся листами. Рисунок 3 иллюстрирует некоторые прямоугольники, организованные в R-дерево Гильберта. Гильбертовы расстояния центров — это числа около символов «x» (показаны только для родительского узла «II»). Значения LHV даны в [скобках]. Рисунок 4 показывает, как дерево из рисунка 3 запоминается на диске. Содержимое родительского узла «II» показано более детально. Любой прямоугольник данных узла «I» имеет значение v ≤33. Аналогично, любой прямоугольник узла «II» имеет гильбертово расстояние, большее 33 и меньшее 107, и т.д..

Рисунок 3: Прямоугольники данных, организованные в R-дерево Гильберта (Гильбертовы расстояния и значения LHV указаны в скобках)

Простое R-дерево разбивает узел при переполнении, создавая два узла. Эта политика называется политикой разбиения 1-в-2. Можно отложить разбиение и преобразовать два узла в три. Заметим, что такая политика подобна политике разбиения B*-деревьев. Такой метод называется политикой разбиения 2-в-3. В общем случае можно говорить о политике разбиения s-в-(s+1), где s — порядок политики разбиения. Для осуществления политики разбиения порядка s переполненный узел пытаются поместить некоторые узлы в один из его s - 1 родственников (узлов на том же уровне). Если все они заполнены, то нужно выполнить разбиение s-в-(s+1). Эти s -1 родственников называются кооперированными узлами. Ниже описаны алгоритмы поиска, вставки и обработки переполнения детально.

Поиск

Алгоритм поиска подобен алгоритмам в других вариантах R-деревьев. Начав с корня, алгоритм опускается по дереву и проверяет все дуги, пересекающие прямоугольник поиска. На листе алгоритм включает все элементы, входящие в окно запроса w как найденные.

Процедура Найти(узел Root, прямоугольник w):
S1. Ищем узлы, не являющиеся листами:

Запускаем поиск для каждого элементы, MBR которого попадает в окно запроса w.

S2. Поиск листьев:

Перечисляем все элементы, которые попадают в окно запроса w в качестве кандидатов.

Рисунок 4: Структура файла R-дерева Гильберта

Вставка

Для вставки нового прямоугольника r в R-дерево Гильберта гильбертово расстояние h центра нового прямоугольника используется в качестве ключа. На каждом уровне среди всех элементов уровня выбирается узел с минимальным значением LHV, превосходящим h. В случае достижения листа прямоугольник r вставляется в него в правильном порядке согласно значению h. После того, как новый прямоугольник вставлен в лист N, запускается процедура СогласованиеДерева для изменения значений MBR и LHV в узлах более высоких уровней.

Процедура Вставить(узел Root, прямоугольник r): /* Вставляет новый прямоугольник r в R-дерево Гильберта.
h является гильбертовым расстоянием прямоугольника*/
I1. Находим подходящий лист:

Вызываем ПоискЛиста(r, h) для выбора листа L, в который включить r.

I2. Вставить r в листe L:

Если L имеет пустой слот, вставляем r в L

в подходящее место согласно порядку гильбертовых расстояний и возвращаемся.

Если L заполнен, вызываем процедуру ОбрабатываемПереполнение(L,r),

которая возвращает новый лист, если разбиение необходимо,

I3. Распространяем изменения:

Образуем множество S, содержащих L, кооперированные узлы

и новый лист (если таковой есть)

Запускаем процедуру СогласованиеДерева (S).

I4. Увеличиваем высоту дерева:

Если распространение изменений вызывает расщепления корня, создаём

новый корень, детьми которого являются два узла, полученные в результате разбиения корня.

Процедура ПоискЛиста(прямоугольник r, целое h):
/* Возвращает лист, в котором следует разместить новый прямоугольник r. */
C1. Инициализация:

Устанавливаем N в качестве корня.

C2. Проверка листа:

Если N является листом, возвращаем N.

C3. Выбираем поддерево:

Если N не является листом, выбираем элемент (R, ptr, LHV)

с минимальным LHV, превосходящим h.

C4. Опускаемся, пока не достигнем листа:

Устанавливаем N на узел, на который указывает ptr и повторяем процесс с точки C2.

Процедура СогласованиеДерева (множество S):
/* S является множеством узлов, содержащих узлы, которые будут изменены,
их кооперированные узлы (если случилось переполнение)
и созданный узел NN (если было осуществлено расщепление узла).
Процедура поднимается от листа к корню, изменяя MBR и LHV узлов, покрывающих узлы в S.
Процедура обрабатывает расщепления узлов (если были) */
A1. Если достигли корня, останавливаемся.
A2. Обрабатываем расщепления узла:

Пусть Np является родителем узла N.

Если узел N был расщеплён, пусть NN будет новым узлом.

Вставляем NN в Np в правильном порядке согласно его гильбертовому расстоянию,

если есть место.

В противном случае вызываем процедуру ОбработкаПереполнения(Np , NN ).

Если узел Np был расщеплён, пусть PP — новый узел.

A3. Изменяем значения MBR и LHV на родительском уровне:

Пусть P — множество родительских узлов для узлов из S.

Изменяем соответствующие значения MBR и LHV в узлах P.

A4. Передвигаемся на следующий уровень:

S становится множеством родительских узлов P,

NN = PP, если Np был расщеплён.

переходим на A1.

Удаление

В R-дереве Гильберта нет необходимости повторной вставки висячих узлов, пока родительский узел не исчезнет. Вместо этого ключи, которые могут быть взяты из нижележащих узлов, сливаются с элементами того же уровня. Это возможно, поскольку узлы имеют ясное упорядочение (согласно LHV). В отличие от этого, для R-деревьев не существует такой концепции. Заметим, что операция удаления требует s кооперированных узлов, в то время как операция вставки требует s - 1 элементов.

Процедура Удалить(r):
D1. Находим лист:

Осуществляем поиск на точное вхождение листа L,

который содержит r.

D2. Удаляем r :

Удаляем r из узла L.

D3. Если L опустевает

берём некоторые элементы из кооперированных узлов.

если таких элементов нет,

приводим s + 1 узлов к s узлам,

пересчитываем полученные узлы.

D4. Изменяем значения MBR и LHV на родительских уровнях.

образуем множество S, содержащее L и его кооперированные

узлы (если случилось переполнение).

вызываем СогласованиеДерева(S).

Обработка переполнения

Процедура обработки переполнения в R-дереве Гильберта обрабатывает переполняемые узлы либо переносом некоторых элементов в один из s - 1 кооперированных узлов или путём расщепления s узлов на s +1 узлов.

Процедура ОбработкаПереполнения(узел N, прямоугольник r):
/* возвращает новый узел, если расщепление произошло. */
H1. Пусть ε — множество, содержащее все элементы из N

и его s - 1 кооперированных узлов.

H2. Добавляем r к ε.
H3. Если по меньшей мере один из s - 1 кооперированных узлов не заполнен,

распределяем ε равномерно по s согласно гильбертовым расстояниям.

H4. Если все s кооперированных узлов заполнены,

создаём узел NN и распределяем ε равномерно

по s + 1 узлам согласно гильбертовым расстояниям

возвращаем NN.

Примечания

1. Kamel, Faloutsos, 1993, с. 490-499.
2. Jagadish, 1990, с. 332-342.
3. Griffiths, 1986, с. 403-411.
4. Bially, 1969, с. 658-664.
5. Beckmann, Kriegel, Schneider, Seeger, 1990, с. 322.

Литература

• I. Kamel, C. Faloutsos. Second International ACM Conference on Information and Knowledge Management (CIKM). — Washington D.C.,, 1993.
• I. Kamel, C. Faloutsos. Proc. of ACM SIGMOD Conf.. — San Diego, CA, 1992. Статья доступна также как Технический отчёт UMIACS TR 92-1, CS-TR-2820.
• I. Kamel, C. Faloutsos. Proc. of VLDB Conf. — Santiago, Chile, 1994. Статья доступна также как Технический отчёт UMIACS TR 93-12.1 CS-TR-3032.1.
• I. Kamel, C. Faloutsos, I. Kamel. International Conference on Extending Database Technology (EDBT). — 1996.
• N. Roussopoulos, D. Leifker. In Proc. of ACM SIGMOD. — Austin, TX, 1985.
• M. Schroeder. Fractals, Chaos, Power Laws: Minutes From an Infinite Paradise. — New York: W.H. Freeman and Company, 1991.
• T. Sellis, N. Roussopoulos, C. Faloutsos. Proc. 13th International Conference on VLDB. — England, 1987.
• H.V. Jagadish. Proc. of ACM SIGMOD Conf.. — Atlantic City, NJ, 1990.
• J. Griffiths. An algorithm for displaying a class of space-filling curves // Software-Practice and Experience. — 1986. — Т. 16, вып. 5.
• T. Bially. IEEE Trans. on Information Theory. — 1969. — Т. IT15.
• N. Beckmann, H. P. Kriegel, R. Schneider, B. Seeger. The R*-tree: an efficient and robust access method for points and rectangles // Proceedings of the 1990 ACM SIGMOD international conference on Management of data - SIGMOD '90. — 1990. — С. 322. — ISBN 0897913655. — doi:10.1145/93597.98741.