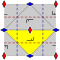
Список плоских групп симметрии

В статье суммируется информация о классах дискретных групп симметрии евклидовой плоскости. Группы симметрии, приведённые здесь, именуются по трём схемам именования: международная нотация, орбифолдная нотация^[англ.] и нотация Коксетера^[англ.]. Существует три вида групп симметрии на плоскости:

• 2 бесконечных семейства точечных групп
• 7 групп бордюра – 2D-рёберные группы^[англ.]
• 17 групп обоев – 2D-пространственные группы.

Точечные группы симметрии

Основная статья: Точечная группа симметрии

На плоскости имеется точка, инвариантная относительно каждого преобразования. Существует два бесконечных семейства дискретных двумерных точечных групп. Группы определяются параметром n, равным порядку подгруппы вращений. Также параметр n равен показателю группы.

Семейство	Межд. (орбифолд^[англ.])	Шёнфлиса	Геом. [1] Коксетер^[англ.]	Порядок	Примеры
Циклические группы	n (n•)	Cn	n [n]^+	n	C1, [ ]^+ (•)	C2, [2]^+ (2•)	C3, [3]^+ (3•)	C4, [4]^+ (4•)	C5, [5]^+ (5•)	C6, [6]^+ (6•)
Диэдральные группы	nm (*n•)	Dn	n [n]	2n	D1, [ ] (*•)	D2, [2] (*2•)	D3, [3] (*3•)	D4, [4] (*4•)	D5, [5] (*5•)	D6, [6] (*6•)

Группа бордюров

На плоскости имеется прямая, которая переходит в себя при каждом преобразовании. При этом отдельные точки этой прямой могут не оставаться неподвижными.

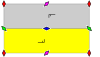
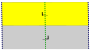
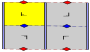
7 групп бордюров, двумерных рёберных групп^[англ.]. Символы Шёнфлиса даны как бесконечные пределы 7 диэдральных групп. Жёлтые области представляют бесконечные фундаментальные области для каждого бордюра.

[1,∞],

IUC (орбифолд^[англ.])	Геом.	Шёнфлис	Коксетер^[англ.]	Фундаментальная область	Пример
p1 (∞•)	p1	C∞	[1,∞]^+
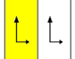p1m1 (*∞•)	p1	C∞v	[1,∞]

[2,∞⁺],

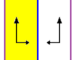IUC (Орбифолд)	Геом.	Шёнфлис	Коксетер	Фундаментальная область	Пример
p11g (∞×)	p.g1	S2∞	[2^+,∞^+]
p11m (∞*)	p. 1	C∞h	[2,∞^+]

[2,∞],

IUC (Орбифолд)	Геом.	Шёнфлис	Коксетер	Фундаментальная область	Пример
p2 (22∞)	p2	D∞	[2,∞]^+
p2mg (2*∞)	p2g	D∞d	[2^+,∞]
p2mm (*22∞)	p2	D∞h	[2,∞]

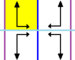Группы обоев

17 групп обоев с конечными фундаментальными областями, упорядоченные по международной нотации, орбифолдной нотации^[англ.] и нотации Коксетера^[англ.] и классифицированы 5 решётками Браве на плоскости: квадратной, скошенной (параллелограммной), шестиугольной (ромбы с углами 60 градусов), прямоугольной и ромбической.

Группы p1 и p2 с зеркальной симметрией встречаются во всех классах. Связанная чистая группа Коксетера отражений дана для всех классов, за исключением косых.

Квадрат [4,4], IUC (Орб.^[англ.]) Геом. Коксетер^[англ.] Фундаментальная область p1 (°) p1 p2 (2222) p2 [4,1^+,4]^+ [1^+,4,4,1^+]^+ pgg (22×) pg2g [4^+,4^+] pmm (*2222) p2 [4,1^+,4] [1^+,4,4,1^+] cmm (2*22) c2 [(4,4,2^+)] p4 (442) p4 [4,4]^+ p4g (4*2) pg4 [4^+,4] p4m (*442) p4 [4,4]

Прямоугольный [∞h,2,∞v], IUC (Orb.) Геом. Коксетер Фундаментальная область p1 (°) p1 [∞^+,2,∞^+] p2 (2222) p2 [∞,2,∞]^+ pg(h) (××) pg1 h: [∞^+,(2,∞)^+] pg(v) (××) pg1 v: [(∞,2)^+,∞^+] pgm (22*) pg2 h: [(∞,2)^+,∞] pmg (22*) pg2 v: [∞,(2,∞)^+] pm(h) (**) p1 h: [∞^+,2,∞] pm(v) (**) p1 v: [∞,2,∞^+] pmm (*2222) p2 [∞,2,∞]

Ромбический [∞h,2^+,∞v], IUC (Orb.) Геом. Коксетер Фундаментальная область p1 (°) p1 [∞^+,2^+,∞^+] p2 (2222) p2 [∞,2^+,∞]^+ cm(h) (*×) c1 h: [∞^+,2^+,∞] cm(v) (*×) c1 v: [∞,2^+,∞^+] pgg (22×) pg2g [((∞,2)^+)^[2]] cmm (2*22) c2 [∞,2^+,∞] Параллелограммный (косой) p1 (°) p1 p2 (2222) p2

Шестиугольная/Треугольная [6,3], / [3^[3]], p1 (°) p1 p2 (2222) p2 [6,3]^Δ cmm (2*22) c2 [6,3]^⅄ p3 (333) p3 [1^+,6,3^+] [3^[3]]^+ p3m1 (*333) p3 [1^+,6,3] [3^[3]] p31m (3*3) h3 [6,3^+] p6 (632) p6 [6,3]^+ p6m (*632) p6 [6,3]

Взаимосвязь подгрупп обоев

В приведенной ниже таблице на пересечении строки, соответствующей группе ${\displaystyle G}$, и столбца, соответствующего группе ${\displaystyle H}$, находится минимальный индекс подгруппы ${\displaystyle G}$, изоморфной ${\displaystyle H}$. На диагонали находится минимальный индекс собственной подгруппы, изоморфной объемлющей группе.

Взаимосвязь подгрупп 17-и групп обоев ^[2]

		o	2222	××	**	*×	22×	22*	*2222	2*22	442	4*2	*442	333	*333	3*3	632	*632
		p1	p2	pg	pm	cm	pgg	pmg	pmm	cmm	p4	p4g	p4m	p3	p3m1	p31m	p6	p6m
o	p1	2
2222	p	2	2	2
××	pg	2		2
**	pm	2		2	2	2
*×	cm	2		2	2	3
22×	pgg	4	2	2			3
22*	pmg	4	2	2	2	4	2	3
*2222	pmm	4	2	4	2	4	4	2	2	2
2*22	cmm	4	2	4	4	2	2	2	2	4
442	p4	4	2								2
4*2	p4g	8	4	4	8	4	2	4	4	2	2	9
*442	p4m	8	4	8	4	4	4	4	2	2	2	2	2
333	p3	3												3
*333	p3m1	6		6	6	3								2	4	3
3*3	p31m	6		6	6	3								2	3	4
632	p6	6	3											2			4
*632	p6m	12	6	12	12	6	6	6	6	3				4	2	2	2	3

См. также

• Список групп сферической симметрии
• Гиперболическая плоскость^[англ.] — Гиперболические группы симметрии

Примечания

1. Hestenes, Holt, 2007.
2. H. S. M. Coxeter, W. O. J. Moser. Generators and Relations for Discrete Groups. Berlin:Springer, 1972. § 4.6, Table 4

Литература

• D. Hestenes^[англ.], J. Holt. The Crystallographic Space groups in Geometric algebra // Journal of Mathematical Physics.. — 2007. — Т. 48, 023514.
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. The Symmetries of Things. — A.K. Peters, 2008. — ISBN 978-1-56881-220-5. (Orbifold notation for polyhedra, Euclidean and hyperbolic tilings)

• John H. Conway, Derek A. Smith. On Quaternions and Octonions: Their geometry, arithmetic, and symmetry. — Natick, MA: A K Peters, Ltd., 2003. — ISBN 978-1-56881-134-5.
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
• Coxeter, H. S. M. and Moser, W. O. J. Generators and Relations for Discrete Groups. — New York: Springer-Verlag, 1980. — ISBN 0-387-09212-9.
• N.W. Johnson. Chapter 11: Finite symmetry groups // Geometries and Transformations. — 2015.

Ссылки

• "Conway's manuscript" on Orbifold notation (Notation changed from this original, x is now used in place of open-dot, and o is used in place of the closed dot)
• The 17 Wallpaper Groups