Цепь Чуа

Рисунок 1. Эквивалентная схема для цепи Чуа^[1] состоящая из линейных пассивных элементов: катушки индуктивности (L), проводимости (G) и двух конденсаторов (C1, C2), а g — нелинейный элемент называемый диодом Чуа. В классическом варианте предлагаются следующие значения элементов: L = 1/7 Гн; G = 0,7 См; C1 = 1/9 Ф; C2 = 1 Ф.

Цепь Чуа или схема Чуа — простейшая электрическая цепь, демонстрирующая режимы хаотических колебаний. Была предложена профессором Калифорнийского университета Леоном Чуа^[англ.] в 1983 году^[1]. Цепь состоит из двух конденсаторов, одной катушки индуктивности, линейного резистора и нелинейного резистора с отрицательным сопротивлением (обычно называемого диодом Чуа)^[2].

Математическая модель

Систему уравнений для цепи изображённой на рисунке 1 можно получить используя первое правило Кирхгофа и формулу для напряжения на катушке индуктивности:

${\displaystyle \left\{{\begin{aligned}C_{1}{\frac {dv_{C_{1}}}{dt}}&=G(v_{C_{2}}-v_{C_{1}})-g(v_{C_{1}}),\\C_{2}{\frac {dv_{C_{2}}}{dt}}&=G(v_{C_{1}}-v_{C_{2}})+i_{L},\\L{\frac {di_{L}}{dt}}&=-v_{C_{2}},\end{aligned}}\right.}$

где ${\displaystyle v_{C_{1}}}$ и ${\displaystyle v_{C_{2}}}$ — напряжения на ёмкостях, ${\displaystyle i_{L}}$ — ток через катушку идуктивности, ${\displaystyle g(v_{C_{1}})}$ — кусочно-линейная функция характеризующая диод Чуа, определённая как^[3]

${\displaystyle g(v_{C_{1}})=G_{b}v_{C_{1}}+{\frac {1}{2}}(G_{a}-G_{b}){\big (}|v_{C_{1}}+E|-|v_{C_{1}}-E|{\big )}\,.}$

Рисунок 2. Вольт-амперная характеристика диода Чуа^[3]. Также показана нагрузочная прямая, от пересечения с которой образуются три точки равновесия d, 0 и −d

Эта нелинейная функция представлена графически на рисунке 2: крутизна внутреннего и внешнего участков есть G_a и G_b соответственно; при этом точки ±Е соответствуют изломам на графике.

Выполним следующие замены на безразмерные коэффициенты:

${\displaystyle m_{0}={\frac {G_{a}}{G}},\quad m_{1}={\frac {G_{b}}{G}},\quad \alpha ={\frac {C_{2}}{C_{1}}},\quad \beta ={\frac {C_{2}}{LG^{2}}}\,,}$

${\displaystyle \tau ={\frac {tG}{C_{2}}},\quad x={\frac {v_{C_{1}}}{E}},\quad y={\frac {v_{C_{2}}}{E}},\quad z={\frac {i_{L}}{EG}}\,.}$

Основная система уравнений запишется в виде

${\displaystyle \left\{{\begin{aligned}{\frac {dx}{d\tau }}&=\alpha {\big (}y-x-h(x){\big )},\\{\frac {dy}{d\tau }}&=x-y+z,\\{\frac {dz}{d\tau }}&=-\beta y,\end{aligned}}\right.}$

где

${\displaystyle h(x)=m_{1}x+{\frac {1}{2}}(m_{0}-m_{1}){\big (}|x+1|-|x-1|{\big )}\,.}$

Режимы работы

Цепь Чуа обнаруживает хаотические режимы колебаний в довольно узкой области параметров. Основные режимы колебаний условно показаны на рисунке 3.

Рисунок 3. Бифуркационная диаграмма режимов при m₀ = −8/7, m₁ = −5/7

В случае, когда параметры α и β принадлежат области, обозначенной на диаграмме цифрой 1, в системе существуют два устойчивых положения равновесия d и −d и одно неустойчивое, находящееся в начале координат 0. В этом случае цепь Чуа в зависимости от начальных условий будет стремиться к одному из двух устойчивых положений равновесия. В случае, когда параметры системы находятся в области помеченной цифрой 2, в окрестности точки равновесия d или −d существует устойчивый предельный цикл. По мере приближения к границе с хаотическим режимом система претерпевает цикл удвоений периода вплоть до образования хаотического аттрактора Рёсслера. Приращение значений параметра перед наступлением каждой последующей бифуркации удвоения периода уменьшается согласно соотношению Фейгенбаума. При попадании параметров в область, помеченную цифрой 6, образуется странный аттрактор (рисунок 4), называемый «двойной завиток» (англ. double scroll). При этом типе поведения траектория система проходит в окрестности и верхнего, и нижнего положения равновесия. Внутри области существования аттрактора «двойной завиток» также существуют окна периодичности, подобные тем, которые существовали в области аттрактора Рёсслера. Отличием их является то, что периодическая орбита в этом случае охватывает оба положения равновесия. Когда параметры α и β переходят в область, помеченную на рисунке 3 цифрой 11, в колебательной системе наблюдаются колебания неограниченно нарастающей амплитуды вне зависимости от начальных условий. Поскольку диод Чуа реализуется на операционных усилителях, он имеет ограниченный динамический диапазон, и поэтому в системе существует также большой по размерам устойчивый предельный цикл, охватывающий все сегменты характеристики диода Чуа.

На рисунках 5, 6 показаны временные зависимости колебаний, обнаруживаемых данной системой.

• 
  Рисунок 4. Аттрактор типа двойной завиток. Фигура Лиссажу i_L от v_С1 при L = 1/7 Гн; G = 0,7 См; C1 = 1/9 Ф; C2 = 1Ф; G_a = −0,8 А/В; G_b = −0,5 А/В
• 
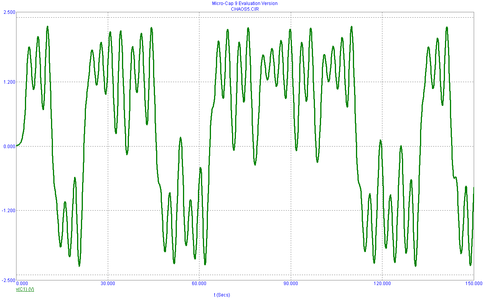
  Рисунок 5. Временная зависимость v_C1 для случая L = 1/7 Гн; G = 0,7 См; C1 = 1/9Ф; C2 = 1Ф; G_a = −0,8 А/В; G_b = −0,5 А/В
• 
  Рисунок 6. Временная зависимость v_C2 для случая L = 1/7 Гн; G = 0,7 См; C1 = 1/9 Ф; C2 = 1 Ф; G_a = −0,8 А/В; G_b = −0,5 А/В

Самовозбуждающиеся и скрытые аттракторы в цепи Чуа

В стандартных физических экспериментах запуск цепи Чуа при замыкании происходит из окрестности нулевых начальных данных. Гипотеза Чуа заключалась в том, что развитие хаоса в цепи и рождение аттрактора возможны только из неустойчивого нулевого состояния равновесия. К настоящему времени в цепи Чуа открыты сотни различных таких самовозбуждающихся аттракторов^[4].

В 2009 году Н. В. Кузнецовым была предложена идея построения скрытого аттрактора Чуа, который сосуществует с устойчивым состоянием равновесия и его область притяжения не касается состояний равновесия, поэтому выбор начальных данных для его визуализации не очевиден^[5][6] . В дальнейшем были обнаружены различные конфигурации скрытых аттракторов в цепи Чуа и проведен бифуркационный анализ их рождения^[7][2].

Осциллятор Чуа

Термин «Осциллятор Чуа» используется для рассмотрения цепи Чуа с учётом активного сопротивления катушки индуктивности L. Данная схема имеет ещё большее число разнообразных режимов и может быть реализована практически (рисунок 7).

Рисунок 7. Практическая схема осциллятора Чуа. L1 = 8,5 мГн, C1 = 4,8 нФ, C2 = 69 нФ, R = 1,3 кОм

Принимая R₀ — активное сопротивление катушки индуктивности L, получим систему уравнений^[3]

${\displaystyle \left\{{\begin{aligned}C_{1}{\frac {dv_{c_{1}}}{dt}}&=G(v_{C_{2}}-v_{C_{1}})-g(v_{C_{1}}),\\C_{2}{\frac {dv_{c_{2}}}{dt}}&=G(v_{C_{1}}-v_{C_{2}})+i_{L},\\L{\frac {di_{L}}{dt}}&=-v_{C_{2}}+R_{0}i_{L}.\end{aligned}}\right.}$

Лёгкость практической реализации, а также наличие относительно простой математической модели делает цепь Чуа удобной моделью для изучения хаоса.

См. также

Мемристор

Примечания

1. Бугаевский, Пономаренко, 1998, с. 4.
2. Kuznetsov N. V.; Mokaev T. N.; Ponomarenko V. I.; Seleznev E. P.; Stankevich N. V.; Chua L. (2017). "Hidden attractors in Chua circuit: mathematical theory meets physical experiments" (PDF). Nonlinear Dynamics. doi:10.1007/s11071-022-08078-y. Архивировано (PDF) 21 декабря 2022. Дата обращения: 21 декабря 2022.
3. Бугаевский, Пономаренко, 1998, с. 5.
4. Bilotta, E. Gallery of Chua Attractors / Bilotta, E., Pantano, P.. — World Scientific, 2008. — ISBN 978-981-279-062-0.
5. Leonov G. A.; Vagaitsev V. I.; Kuznetsov N. V. (2011). "Localization of hidden Chua's attractors" (PDF). Physics Letters A. 375 (23): 2230–2233. Bibcode:2011PhLA..375.2230L. doi:10.1016/j.physleta.2011.04.037. Архивировано (PDF) 19 января 2022. Дата обращения: 21 декабря 2022.
6. Leonov G. A.; Kuznetsov N. V. (2013). "Hidden attractors in dynamical systems. From hidden oscillations in Hilbert–Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits". International Journal of Bifurcation and Chaos. 23 (1): 1330002–219. Bibcode:2013IJBC...2330002L. doi:10.1142/S0218127413300024.
7. Stankevich N. V.; Kuznetsov N. V.; Leonov G. A.; Chua L. (2017). "Scenario of the birth of hidden attractors in the Chua circuit". International Journal of Bifurcation and Chaos. 27 (12): 1730038–188. arXiv:1710.02677. Bibcode:2017IJBC...2730038S. doi:10.1142/S0218127417300385. S2CID 45604334.

Литература

• Кузнецов А. П. Наглядные образы хаоса // Соросовский образовательный журнал, 2000, № 11, с. 104—110;
• Бугаевский М. Ю., Пономаренко В. И. Исследование поведения цепи Чуа. Учебно-методическое пособие. — Саратов: Издательство ГосУНЦ «Колледж», 1998. — 29 с.
• Matsumoto, T. A Chaotic Attractor from Chua’s Circuit, IEEE Transactions on Circuits & Systems,1984, vol. CAS-31, no. 12, pp. 1055—1058.
• Chua, L. O., Komuro, M., Matsumoto, T. «The Double Scroll Family», IEEE Transactions on Circuits & Systems, 1986, vol. CAS-33, no. 11, pp. 1073—1118.
• T. Matsumoto, L. O. Chua, M. Komuro. «Birth and death of the double scroll», Physica D Volume 24 , Issue 1-3 (Jan/Feb 1987).
• Stankevich N. V.; Kuznetsov N. V.; Leonov G. A.; Chua L. (2017). «Scenario of the birth of hidden attractors in the Chua circuit». International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. 27 (12): 1730038-188 https://doi.org/10.1142/S0218127417300385
• Н. В. Кузнецов. Теория скрытых колебаний и устойчивость систем управления // Известия РАН. Теория и Системы управления. — 2020. — № 5. — С. 5—27. — doi:10.31857/S0002338820050091.

Ссылки

• Chua’s Circuit diagrams, equations, simulation and pictures Чуа Схемы, формулы, моделирования и фотографии
• Chua’s Circuit: Diagram and discussion
• NOEL laboratory. Leon O. Chua’s laboratory at the University of California, Berkeley
• References
• ТИИЭР Том 75 № 8 Август 1987