Enakokraki pravokotni trikotnik

Enakokraki pravokotni trikotnik

Očrtana in včrtana krožnica enakokrakemu pravokotnemu trikotniku. Razdalja med središčema krožnic je enaka ${\displaystyle d=r\,}$.

Enakokraki pravokotni trikotnik in enakokraki trikotnik z enakima očrtano in včrtano krožnico in enako razdaljo med njunima središčema ${\displaystyle d=r\,}$.

Enakokráki pravokótni trikótnik^{[1]:§3, 70} (redkeje tudi pravokotni enakokraki trikotnik ali trikotnik 45-45-90) je glede na stranice posebni primer enakokrakega, oziroma glede na notranje kote pravokotnega trikotnika, kjer sta notranja kota ob osnovnici enako velika (skladna) in enaka 45°:

${\displaystyle \alpha =\beta =45^{\circ }={\frac {\pi }{4}}\!\,,}$

tretji notranji kot pa je pravi:

${\displaystyle \gamma =180^{\circ }-2\alpha =90^{\circ }={\frac {\pi }{2}}\!\,,}$

tako, da so si notranji koti v razmerju 1 : 1 : 2.

Kraka sta enaka:

${\displaystyle a=b={\frac {c{\sqrt {2}}}{2}}\!\,,}$

osnovnica pa:

${\displaystyle c=a{\sqrt {2}}\!\,,}$

in so si stranice v razmerju 1 : 1 : √2. Kraka sta hkrati tudi kateti, osnovnica pa je hipotenuza.

Štirje takšni trikotniki tvorijo kvadrat, kjer je njihova osnovnica enaka stranici kvadrata. Če je osnovnica enaka diagonalama kvadrata, kvadrat tvorita dva takšna trikotnika.

Višina na osnovnico je enaka polovici osnovnice:

${\displaystyle v_{c}={\frac {a{\sqrt {2}}}{2}}={\frac {c}{2}}=R\!\,,}$

kjer je R polmer očrtane krožnice. Druga zveza je posledica Talesovega izreka, oziroma izreka o središčnem in obodnem kotu.

Trikotniki s takšnimi notranjimi koti so v evklidski geometriji edini možni pravokotni trikotniki, ki so hkrati tudi enakokraki. V sferni in hiperbolični geometriji pa obstaja neskončno mnogo oblik enakokrakih pravokotnih trikotnikov.

Obseg

Obseg enakokrakega pravokotnega trikotnika je skupna dolžina vseh stranic:

${\displaystyle o=a+b+c=a(2+{\sqrt {2}})\!\,.}$

Ploščina

Ploščina enakokrakega pravokotnega trikotnika je enaka:

${\displaystyle p={\frac {a^{2}}{2}}={\frac {c^{2}}{4}}\!\,.}$

Za ploščino enakokrakega pravokotnega trikotnika velja tudi Heronova formula v obliki:

${\displaystyle p={\sqrt {s(s-a)^{2}(s-a{\sqrt {2}})}}\!\,,}$

kjer je s polovični obseg (polobseg) enakokrakega pravokotnega trikotnika:

${\displaystyle s={\frac {o}{2}}=a\left(1+{\frac {\sqrt {2}}{2}}\right)\!\,.}$

Splošne značilnosti

Očrtana in včrtana krožnica

Enakokraki pravokotni trikotnik je kot vsi trikotniki bicentričen. V njem velja:

${\displaystyle r\!\,}$	${\displaystyle R\!\,}$	${\displaystyle a\!\,}$	${\displaystyle c\!\,}$
${\displaystyle R\left({\sqrt {2}}-1\right)={\frac {a}{2}}\left(2-{\sqrt {2}}\right)={\frac {c}{2}}\left({\sqrt {2}}-1\right)\!\,}$	${\displaystyle {\frac {r}{{\sqrt {2}}-1}}={\frac {a}{2}}{\sqrt {2}}={\frac {c}{2}}\!\,}$	${\displaystyle {\frac {2r}{2-{\sqrt {2}}}}=R{\sqrt {2}}={\frac {c}{2}}{\sqrt {2}}\!\,}$	${\displaystyle {\frac {2r}{{\sqrt {2}}-1}}=2R=a{\sqrt {2}}\!\,}$

Tu je r polmer včrtane krožnice, R polmer očrtane krožnice, a dolžina krakov in c dolžina osnovnice enakokrakega pravokotnga trikotnika.

Nepravilno pokritje evklidske ravnine z enakokrakimi pravokotnimi trikotniki

Poliabole z enim do 5 osnovnimi liki

Štirje enakokraki pravokotni trikotniki skupaj z drugimi sedmimi osnovnimi liki tvorijo Bermudski trikotnik, različico igre sestavljanke tangram

Razdalja med središčema včrtane in očrtane krožnice d je enaka polmeru včrtane krožnice r in je dana z Eulerjevo trikotniško enačbo:

${\displaystyle d^{2}=R(R-2r)={\frac {a^{2}}{2}}\left(3-2{\sqrt {2}}\right)\!\,}$

${\displaystyle d=r={\frac {a}{2}}\left(2-{\sqrt {2}}\right)=a{\sqrt {{\frac {1}{2}}\left(3-2{\sqrt {2}}\right)}}\approx 0,2928932\,a\!\,.}$

Enakokraki trikotnik, ki ima enaki očrtano in včrtano krožnico in enako razdaljo med njunima središčema (${\displaystyle d=r\,}$), ima kote:

${\displaystyle \alpha =\beta =\operatorname {arc\,tg} {\frac {4-{\sqrt {2}}}{{\sqrt {2}}{\sqrt {8{\sqrt {2}}-11}}}}\approx 72,968751^{\circ }\!\,,}$

${\displaystyle \gamma =180^{\circ }-2\alpha \approx 34,062496^{\circ }\!\,.}$

Pokritje evklidske ravnine

Enakokraki pravokotni trikotnik je eden od treh trikotnikov, ki pokrijejo evklidsko ravnino. Le z enakostraničnim trikotnikom (trikotnik 60–60–60), ki je pravilni mnogokotnik, lahko pravilno pokrijemo ravnino. Tretji trikotnik, ki nepravilno pokrije ravnino, pa je pravokotni trikotnik 30–60–90. Ti trije trikotniki so Möbiusovi trikotniki, kar pomeni, da pokrijejo ravnino brez prekrivanja z zrcaljenjem njihovih stranic (glej trikotniška grupa).

Poliforme in sestavljanke

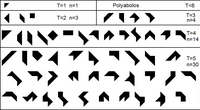
Poliforme, katerih osnovni liki so enakokraki pravokotni trikotniki, so poliabole.

Pet enakokrakih pravokotnih trikotnikov treh različnih velikosti skupaj z enim kvadratom in enim paralelogramom tvori osnovne like igre sestavljanke tangram.

Glej tudi

• Calabijev trikotnik

Sklici

1. Stöcker (2006), §3, str. 70.

Viri

• Stöcker, Horst (2006), Matematični priročnik z osnovami računalništva, Ljubljana: Tehniška založba Slovenije, COBISS 229576192, ISBN 86-365-0587-9, OCLC 449201276

Zunanje povezave

• Weisstein, Eric Wolfgang. »Isosceles Right Triangle«. MathWorld.