Rombitrišestkotno tlakovanje

Robitrišestkotno tlakovanje

Vrsta polpravilno tlakovanje
Konfiguracija oglišča 3.4.6.4
Schläflijev simbol t0,2{6,3}
Wythoffov simbol 3|6 2
Coxeter-Dinkinov diagram
Simetrija p6m, [6,3], *632
Vrtilna simetrija p6, [6,3]+, 632
Bowersova okrajšava Rothat
Dualno tlakovanje deltoidno trišestkotno tlakovanje
Lastnosti ogliščna prehodnost

Slika oglišč: 3.4.6.4

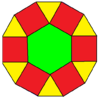
Rombitrišestkotno tlakovanje je v geometriji polpravilno tlakovanje evklidske ravnine. Ima en trikotnik, en šestkotnik in po en šestkotnik na vsakem oglišču (pri tlakovanju je to točka, kjer se stikajo tri ali več ploščic tlakovanja). Schläflijev simbol je t0,2{3,6}.

Znana so tri pravilna tlakovanja in osem polpravilnih tlakovanj v ravnini.

John Horton Conway (rojen 1937) ga je imenoval rombišestdeltil [1]. Lahko ga obravnavamo kot kantelirani ali razširjeno šestkotno tlakovanje.

Uniformno barvanje

[uredi | uredi kodo]

Obstoja samo eno uniformno barvanje rombitrišestkotnega tlakovanja. Če imenujemo barve s števili okoli oglišča (3.4.6.4) je to samo 1232.

Sorodni poliedri in tlakovanja

[uredi | uredi kodo]
Družina Kupol
2 3 4 5 6

diagonalna kupola
tristrana kupola
kvadratna kupola
petstrana kupola
šeststrana kupola
(ravna)

Tlakovanje je topološko povezano z zaporedjem kanteliranimi poliedri, ki imajo sliko oglišč (3.4.n.4) in se nadaljujejo kot tlakovanja v hiperbolično ravnino. Te ogliščnoprehodne oblike imajo (*n32) zrcalno simetrijo.

Sferna/ravninska
simetrija 		*232
[2,3]
D3h 		*332
[3,3]
Td 		*432
[4,3]
Oh 		*532
[5,3]
Ih 		*632
[6,3]
P6m 		*732
[7,3] 		*832
[8,3]
Red
simetrije 		12 24 48 120 ∞
Coxeter
Schläfli
t0,2{2,3}
t0,2{3,3}
t0,2{4,3}
t0,2{5,3}
t0,2{6,3}
t0,2{7,3}
t0,2{8,3}
Razširjena
oblika
3.4.2.4
3.4.3.4
3.4.4.4
3.4.5.4
3.4.6.4
3.4.7.4
3.4.8.4
Deltoidna oblika
V3.4.2.4
V3.4.3.4
V3.4.4.4
V3.4.5.4
V3.4.6.4
V3.4.7.4

Wythoffova konstrukcija iz šestkotnih in trikotnih tlakovanj

[uredi | uredi kodo]
Wythoff 3 | 6 2 2 3 | 6 2 | 6 3 2 6 | 3 6 | 3 2 6 3 | 2 6 3 2 | | 6 3 2
Schläfli {6,3} t0,1{6,3} t1{6,3} t1,2{6,3} t2{6,3} t0,2{6,3} t0,1,2{6,3} s{6,3} h0{6,3} h1,2{6,3}
Coxeter
Slika
Slika oglišč
6.6.6
3.12.12
3.6.3.6
6.6.6
{36}
3.4.6.4
4.6.12
3.3.3.3.6
(3.3)3
3.3.3.3.3.3

Pakiranje krožnic

[uredi | uredi kodo]

Rombitrišestkotno tlakovanje se lahko uporabi za pakiranje krožnic. Vsaka krožnica je v dotiku s tremi drugimi krožnicami v pakiranju. (glej problem dotikalnega števila). Praznine med šestkotniki dovoljujejo vnos dodatne krožnice, da s tem dobimo gostejše pakiranje.

Opombe in sklici

[uredi | uredi kodo]
  1. ↑ Conway, 2008, p288 table

Zunanje povezave

[uredi | uredi kodo]