Seznam grup sferne simetrije vsebuje grupe sferne simetrije. Te grupe se imenujejo tudi trirazsežna točkovna grupa. Tukaj se obravnavanje omeji samo na končne simetrije.
Znanih je pet osnovnih razredov, ki vsebujejo trikotno osnovno domeno. To so diedrska, ciklična, tetraedrska, oktaedrska in ikozaedrska simetrija.
Grupe so prikazane v skladu z Schönfliesovo notacijo, Coxeterjevo notacijo in notacijo orbifold. Angleški matematik John Horton Conway je uporabil posebno variacijo Schönfliesove notacije.
Dana je tudi Hermann-Mauguinova notacija (mednarodna notacija, tukaj označena z Medn.). Kristalografske grupe, ki jih je 32, so podmnožica z redom elementov enakim 2, 3, 4 ali 6 [1].
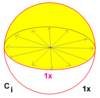
Znane so štiri involucijske grupe. Te grupe so primeri kjer ni simetrije, zrcalne simetrije, 2-kratna simetrije vrtenja in centralne točkovne simetrije.
|
|
| Medn.
|
geo[2]
|
orbifold
|
Schönflies
|
Conway
|
Coxeter
|
red
|
osnovna
domena
|
| 1
|
22
|
×
|
Ci
= S2
|
CC2
|
[2+,2+]
|
2
|
|
2
= m
|
1
|
*
|
Cs
= C1v
= C1h
|
±C1
= CD2
|
[ ]
|
2
|

|
|
Obstajajo štiri družine ciklične simetrije, ki imajo n=2 ali višje. V posebnem primeru je lahko tudi n=1.
| Medn.
|
geo[2]
|
orbifold
|
Schönflies
|
Conway
|
Coxeter
|
red
|
osnovna
domena
|
| 2
|
2
|
22
|
C2
= D1
|
C2
= D2
|
[2]+
|
2
|

|
| mm2
|
2
|
*22
|
C2v
= D1h
|
CD4
= DD4
|
[2]
|
4
|

|
| 4
|
42
|
2×
|
S4
|
CC4
|
[2+,4+]
|
4
|

|
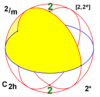
| 2/m
|
22
|
2*
|
C2h
= D1d
|
±C2
= ±D2
|
[2,2+]
|
4
|
|
|
| Medn.
|
geo[2]
|
orbifold
|
Schönflies
|
Conway
|
Coxeter
|
red
|
osnovna
domena
|
3
4
5
6
n
|
3
4
5
6
n
|
33
44
55
66
nn
|
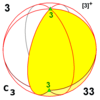
C3
C4
C5
C6
Cn
|
C3
C4
C5
C6
Cn
|
[3]+
[4]+
[5]+
[6]+
[n]+
|
3
4
5
6
n
|
|
3m
4mm
5m
6mm
-
|
3
4
5
6
n
|
*33
*44
*55
*66
*nn
|
C3v
C4v
C5v
C6v
Cnv
|
CD6
CD8
CD10
CD12
CD2n
|
[3]
[4]
[5]
[6]
[n]
|
6
8
10
12
2n
|

|
3
8
5
12
-
|
62
82
10.2
12.2
2n2
|
3×
4×
5×
6×
n×
|
S6
S8
S10
S12
S2n
|
±C3
CC8
±C5
CC12
CC2n / ±Cn
|
[2+,6+]
[2+,8+]
[2+,10+]
[2+,12+]
[2+,2n+]
|
6
8
10
12
2n
|

|
3/m
4/m
5/m
6/m
n/m
|
32
42
52
62
n2
|
3*
4*
5*
6*
n*
|
C3h
C4h
C5h
C6h
Cnh
|
CC6
±C4
CC10
±C6
±Cn / CC2n
|
[2,3+]
[2,4+]
[2,5+]
[2,6+]
[2,n+]
|
6
8
10
12
2n
|

|
|
Obstajajo samo tri družine neskončnih diedrskih simetrij.
| Medn.
|
geo[2]
|
orbifold
|
Schönflies
|
Conway
|
Coxeter
|
red
|
osnovna
domena
|
| 222
|
2.2
|
222
|
D2
|
D4
|
[2,2]+
|
4
|

|
| 42m
|
42
|
2*2
|
D2d
|
DD8
|
[2+,4]
|
8
|

|
| mmm
|
22
|
*222
|
D2h
|
±D4
|
[2,2]
|
8
|

|
|
| Medn.
|
geo [2]
|
orbifold
|
Schönflies
|
Conway
|
Coxeter
|
red
|
osnovna
domena
|
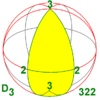
32
422
52
622
|
3.2
4.2
5.2
6.2
n.2
|
223
224
225
226
22n
|
D3
D4
D5
D6
Dn
|
D6
D8
D10
D12
D2n
|
[2,3]+
[2,4]+
[2,5]+
[2,6]+
[2,n]+
|
6
8
10
12
2n
|
|
3m
82m
5m
12.2m
|
62
82
10.2
12.2
n2
|
2*3
2*4
2*5
2*6
2*n
|
D3d
D4d
D5d
D6d
Dnd
|
±D6
DD16
±D10
DD24
DD4n / ±D2n
|
[2+,6]
[2+,8]
[2+,10]
[2+,12]
[2+,2n]
|
12
16
20
24
4n
|

|
6m2
4/mmm
10m2
6/mmm
|
32
42
52
62
n2
|
*223
*224
*225
*226
*22n
|
D3h
D4h
D5h
D6h
Dnh
|
DD12
±D8
DD20
±D12
±D2n / DD4n
|
[2,3]
[2,4]
[2,5]
[2,6]
[2,n]
|
12
16
20
24
4n
|

|
|
Znani so trije tipi poliedrske simetrije. To so tetraedrska, oktaedrska in ikozaedrska simetrija. Imena so simetrije dobile z uporabo pravilnih poliedrov s takšno vrsto simetrije.
[3,3]
| Medn.
|
geo [2]
|
orbifold
|
Schönflies
|
Conway
|
Coxeter
|
red
|
osnovna
domena
|
| 23
|
3.3
|
332
|
T
|
T
|
[3,3]+
= [3+,4,1+]
|
12
|

|
| m3
|
43
|
3*2
|
Th
|
±T
|
[3+,4]
= [[3,3]+]
|
24
|

|
| 43m
|
33
|
*332
|
Td
|
TO
|
[3,3]
= [3,4,1+]
|
24
|

|
|
[3,4]
| Medn.
|
geo [2]
|
orbifold
|
Schönflies
|
Conway
|
Coxeter
|
red
|
osnovna
domena
|
| 432
|
4.3
|
432
|
O
|
O
|
[3,4]+
= [[3,3]]+
|
24
|

|
| m3m
|
43
|
*432
|
Oh
|
±O
|
[3,4]
= [[3,3]]
|
48
|

|
[3,5]
| Medn.
|
geo [2]
|
orbifold
|
Schönflies
|
Conway
|
Coxeter
|
red
|
osnovna
domena
|
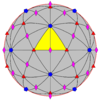
| 532
|
5.3
|
532
|
I
|
I
|
[3,5]+
|
60
|
|
| 532/m
|
53
|
*532
|
Ih
|
±I
|
[3,5]
|
120
|

|
|
- ↑ Sands, 1993
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 The Crystallographic Space groups in Geometric algebra, D. Hestenes in J. Holt, Časopis za matematično fiziko. 48, 023514 (2007) (22 strani) PDF [1] Arhivirano 2020-10-20 na Wayback Machine.























