Hilbertovo R-stablo

Овај чланак је започет или проширен кроз пројекат семинарских радова. Потребно је проверити превод, правопис и вики-синтаксу. Када завршите са провером, допишете да након |проверено=.

Hilbertovo R-stablo, varijanta R-stabla je indikator za višedimenzionalne objekte kao što su linije, regioni, 3-D objekti ili visoko-dimenzionalni objekti zasnovani na parametarskim oblicima. Može se posmatrati kao proširenje B+-stabla za višedimenzionalne objekte. Performanse R-stabla zavise od kvaliteta algoritma koji grupiše pravougaonike podataka na čvoru. Hilbertovo R-stablo koristi prostorno-pune krive, a posebno Hilbertove krive, kako bi na pravougaonike podataka nametnuo linearan redosled. Postoje dve vrste Hilbertovih R-stabala, jedan za statičke, a jedan za dinamičke baze podataka. U oba slučaja Hilbertove prostorno-pune krive se koriste radi psotizanja boljeg redosleda višedimenzionalnih objekata na čvoru. Ovaj redosled mora da bude "dobar", u tom smislu da grupiše zajedno 'slične' pravougaonike podataka, kako bi se smanjio prostor i obim dobijenog. Pakovana Hilbertova R-stabla su pogodna za statičke baze podataka u kojima je ažuriranje podataka veoma retko, ili uopšte nije prisutno. Dinamičko Hilbertovo R-stablo je pogodno za dinamičke baze podataka gde se umetanje, brisanje ili ažuriranje može postići u realnom vremenu. Štaviše, dinamičko Hilbertovo R-stablo upotrebljava fleksibilan mehanizam odloženog razdvajanja, kako bi povećao stepen iskorišćenosti prostora. Svaki čvor ima dobro definisan skup čvorova rođaka. Prilagođavanjem politike podele Hilbertovo R-stablo može postići željeni stepen iskorišćenosti prostora. Ovo se postiže planiranjem uređenosti čvorova na R-stablu. Hilbertovo R-stablo sortira pravougaonike prema Hilbertovoj vrednosti centra pravougaonika. Nasuprot Hilbertovom R-stablu, druge varijante R-stabla nemaju kontrolu nad stepenom iskorišćenosti prostora.

Osnovna ideja

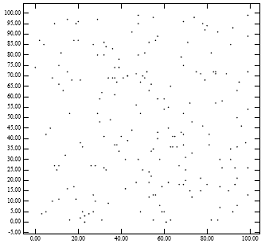
Iako je sledeći primer za statičko okruženje, objašnjava intuitivne principe za dobar dizajn R-stabla. Ovi principi važe i za statičke i za dinamičke baze podataka. Roussopoulos i Leifker su predložili metod za izgradnju pakovanog R-stabla koji postiže stepen od skoro 100% iskorišćenosti prostora. Ideja je sortiranje podataka na x ili y koordinatu jednog ugla pravougaonika. Sortiranje na bilo koju od četiri koordinate daje sličan rezultat. U ovom slučaju, tačke ili pravougaonici su sortirani na x koordinatu najnižeg levog ugla pravougaonika. U diskusiji koja sledi, Roussopoulos-ov i Leifker-ov metod se posmatra kao nisko x pakovano R-stablo. Sortirana lista pravougaonika se pretražuje; uzastopni pravougaonici se dodeljuju istom listu R-stabla sve dok je taj čvor pun; tada se kreira novi list i pretraživanje sortirane liste se nastavlja. Tako će čvorovi rezultujućeg R-stabla biti u celosti upakovani, sa mogućim izuzetkom poslednjeg čvora na svakom nivou. Tako je procenat iskorišćenosti ≈100%. Viši nivoi stabla su kreirani na sličan način. Figura 1 naglašava problem nisko x pakovanog R-stabla. Slika 1[desno] pakazuje listove R-stabla koje će nisko x pakovani metod napraviti za tačke Slike 1 [levo]. Činjenica da dobijeni roditelji pokrivaju malu oblast objašnjava zašto nisko x pakovani metod R- stabla postiže odlične performanse za tačke upita. Međutim, činjenica da roditelji imaju veliki opseg objašnjava degradaciju performanse za predeo upita. Ovo je u skladu sa analitičkim formulama za performanse R-stabla. .^[1] Intuitivno gledano, algoritam pakovanja bi idejno trebao dodeliti obližnje tačke istom listu. Ignorisanje y koordinate u nisko x pakovanom R-stablu preti da naruši ovo empirično pravilo.

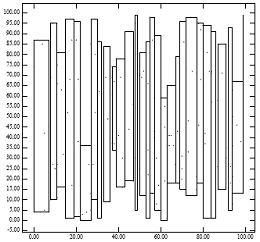
Slika 1: [levo] 200 tačaka ravnomerno raspoređenih; [desno] minimalni granični pravougaonici čvorova generisani ‘nisko x pakovanim ’ algoritmom za R-stablo

Ovaj odeljak opisuje dve varijante Hilbertovog R-stabla. Prvi indikator je pogodan za statičke baze podataka u kojima je ažuriranje veoma retko ili nije prisutno uopšte. Čvorovi rezultujućeg R-stabla će biti celovito upakovani, sa mogućom iznimkom poslednjeg čvora na svakom nivou. Tako je stepen upotrebe prostora ≈100%; ova struktura se naziva pakovano Hilbertovo R-stablo. Drugi indikator se nayiva dinamičko Hilbertovo R-stablo, podržava umetanje i brisanje; pogodan je za dinamičko okruženje.

Pakovana Hilbertova R-stabla

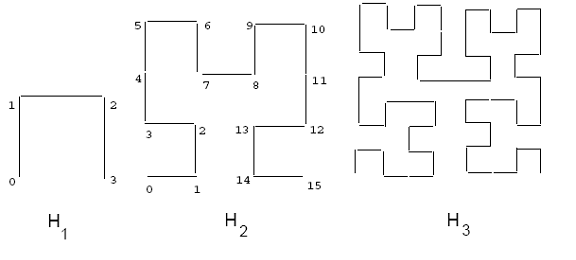
U nastavku je dat kratak uvod ne temu Hilbertove krive. Osnovna Hilbertova kriva na mreži 2x2, označena sa H₁ je pokazana na slici 2. Kako bi izveli krivu reda i, svako teme osnovne krive je zamenjeno krivom reda i – 1, što može biti adekvatno rotirano i/ili reflektovano. Slika 2 takođe pokazuje Hilbertove krive reda dva i tri. Kad red krive teži beskonačnosti, kao druge prostorno pune krive, rezultujuća kriva je strukturalno fraktalna, sa dimenzijom 2.^[1][2] Hilbertova kriva može biti generalizovana za viši stepen dimenzionalnosti. Algoritmi za crtanje 2-dimenzione krive datog reda može biti nađen na^[3] i^[2] Algoritam za veću dimenzionalnost je dat na.^[4] Putanja prostorno pune krive nameće linearni redosled na tačkama mreže; ova putanja može biti izračunata prateći putanju krive sa početkom u jednom kraju, a završetkom u drugom kraju krive. Vrednosti koordinata mogu biti izračunate u svakoj tački. Slika 2 pokazuje jedan takav redosled za mrežu 4x4. Na primer, tačka (0,0) na H₂ krivi ima Hilbertovu vrednost 0, dok tačka (1,1) ima Hilbertovu vrednost 2.

Slika 2: Hilbert-ove krive reda 1, 2 i 3

Hilbertova kriva nameće linearan redosled pravougaonika podataka, a zatim prelazi na sortiranu listu, dodeljujući skup od C pravougaonika svakom čvoru R-stabla. Krajnji rezultat je taj da će skup pravougaonika podataka na istom čvoru biti blizu jedan drugog prema linearnom redosledu i najverovatnij u rodnom prostoru. Dakle, dobijeni čvorovi R-stabla će imati manja područija. Slika 2 ilustruje razloge zbog kojih će metode zasnovane na Hilbertovom R-stablu imati dobru performansu. Podaci se sastoje od tačaka (iste tačke koje su date i na slici 1). Grupisanjem tačaka prema njihovoj Hilbertovoj vrednosti, MGP dobijenih čvorova R-stabla imaju tendenciju da budu mali kvadrati nalik pravougaonicima. Ovo ukazuje da će čvorovi najverovatnije imati malu površinu i male parametre. Mala površina donosi dobre performanse za upite tačaka; mala površina i mali parametri donose dobru performansu za veće upite.

Algoritam Hilbertovog pakovanja

(pakuje pravougaonike na R-stablo)

Korak 1. Računa Hilbertovu vrednost za svaki pravougaonik podatka

Korak 2. Sortira pravougaonike podataka po uzlaznom poretku Hilbertovih vrednosti

Korak 3. /* Pravi listove (nivo l=0) */

• While (ima još pravougaonika)
  • generiši novi čvor R-stabla
  • dodeli sledeći C pravougaonik ovom čvoru

Korak 4. /* Napravi čvorove na višem nivou (l + 1) */

• While (dok su > 1 čvora na novou l)
  • sortiraj čvorove na nivou l ≥ 0 na osnovu uzlaznog poretka vremena potrebnog za kreiranje
  • ponovi korak 3

Pretpostavka je da su podaci statički ili da je frekfencija modifikacije niska. Ovo je jednostavna heruistika za izgradnju R-stabla sa stepenom iskorišćenosti prostora od 100% što će istovremeno imati najbolje moguće vreme odgovora.

Dinamička Hilbertova R-stabla

Performanse R-stabla zavise od kvaliteta algoritma koji grupišu pravougaonike podataka na čvor. Hilbertova R-stabla koriste prostorno pune krive, konkretno Hilbertovu krivu, kako bi nametnula linearni redosled na pravougaonike podataka.

Hilbertova vrednost pravougaonika se definiše kao vrednost njegovog centra.

Struktura stabla

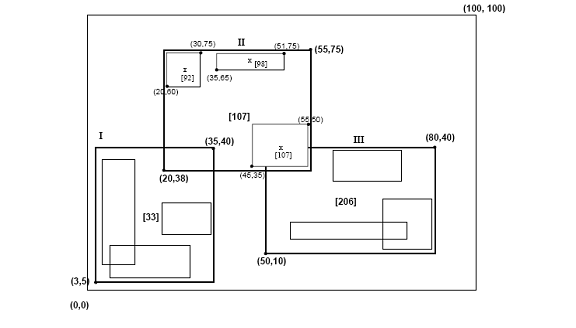
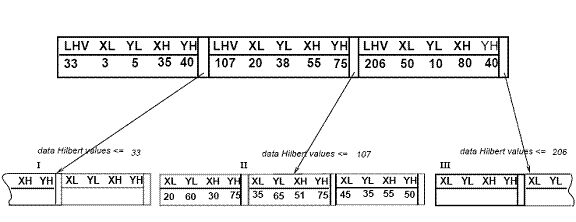
Hilbertovo R-stablo ima sledeću strukturu. List sadrži najviše C_l ulaza, oblika (R, obj _id) gde je C_l kapacitet lista, a R je MGP(minimalni granični pravougaonik) realnog objekta. (x_nisko, x_visoko, y_nisko, y_visoko) i obj-id je pokazivač na objekat koji sadrži zapisnik opisa tog objekta. Glavna razlika izmedju Hilbertovog R-stabla i R*-stabla^[5] je ta da čvorovi koji nisu listovi sadrze informacije o "LHV"(najveća Hilbertova vrednost). Dakle, čvor koji nije list u Hilbertovom R-stablu sadrži najviše C_n ulaza oblika (R, ptr, NHV) gde je C_n kapacitet čvora koji nije list, R je "MGP" koji obuhvata svu decu tog čvora, "ptr" je pokazivač na dete čvora, "NHV" je najveća Hilbertova vrednost između pravouganika podataka obuhvaćenih sa R. Treba primetiti da čvor koji nije list bira jednu od Hilbertovih vrednosti njegove dece i postavlja je za sopstvenu "NHV" vrednost. Ne postoji dodatna cena za izračunavanje Hilbertovih vrednosti MGP-a za čvorove koji nisu listovi. Slika 3 ilustruje neke pravoukaonike organizovane u Hilbertovim R-stablima. Hilbertove vrednosti centra su brojevi blizu 'x' simbola(prikazuje se samo za čvora pretka 'II')."NHV" su prikazani u [zagradama]. Slika 4 prikazuje kako se stablo sa slike 3 čuva na disku. Sadržaji čvora pretka 'II' su prikazani sa više detalja. Svaki pravouganik podataka u čvoru 'I' ima Hilbertovu vrednost v≤33.

Slika 3: ilustruje neke pravoukaonike organizovane u Hilbertovim R-stablima. (Hilbertove vrednosti i NHV su prikazane u zagradama) Obično R-stablo deli čvor na dva dela ukoliko dođe do "prelivanja" na tom čvoru, praveći 2 nova čvora od prvobitnog. Ova politika se zove 1-na-2 politika cepanja. Takođe je moguće da se odloži rascep, čekajući da se dva čvora pretvore u tri. Uočite da je ovo slično sa B*-politikom cepanja stabla. Ovaj metod se zove 2-na-3 politika cepanja. Generalno, ovo se može proširiti na s-na-(s+1) politika cepanja, gde je s naređenje za politiku cepanja. Za implementaciju politike cepanja, "preliveni" čvor gura neke od njegovih ulaza na s-1 rođake. Algoritmi za pretraživanje, ubacivanje i "rukovanje prelivenim" su opisani detajno u daljem tekstu.

Traženje

Algoritam traženja je sličan algoritmima traženja korišćenim u drugim varijantama R-stabla. Počevši od korena, spušta se niz stablo i ispituje sve čvorove koji seku pravougaonike upita. Na nivou lista, prijavljuje sve ulaze koji seku prozore w upita kao kvalifikovane stavke podataka.

Algoritam Traženje(koren, pravougaonik w):

S1. Traži čvorove koji nisu listovi:

Zovi Traži za svaki ulaz čiji MGP seče prozor w upita.

Prijavi kao kandidate sve ulaze koji seku prozor w upita.

Figura 4: Struktura fajla za Hilbertovo R-stablo

Umetanje

Za umetanje novog pravougaonika r u Hilbertovo R-stablo, Hilbertova vrednost h od centra novog pravougaonika se koristi kao ključ. Na svakom nivou izabran je čvor sa najmanjom NHV vrednošću većom od h. Kada je dosegnut list, pravougaonik r je umetnut po odgovarajućem rasporedu prema h. Nakon što je novi pravougaonik umetnut u list N, pozvano je podesi stablo kako bi popravilo vrednosti MGP i LHV na čvorovima većeg nivoa.

Algoritam Umetni(koren, pravougaonik r): /* Ubacuje novi pravougaonik r u Hilbertovo R-stablo. h je Hilbertova vrednost pravougaonika*/

I1. Pronađi pogodan list.:

Pozovi Izaberi_list(r, h) kako bi izabrao list L u koji će biti smešten r.

I2. Ubaci r u list L:

Ako L ima prazan prorez, ubaci r u L na odgovarajućem mestu prema Hilbertovom redu i vrati se.

Ako je L puno, pozovi Rukovanje_prelivenim(L,r), što će vratiti novi list ako je razdvajanje bilo neizbežno.

I3. Propagirati promene nagore:

Formirati skup S koji sadrži L, njegove rođake

i novi list (ako postoji)

Prizovi podesi_stablo(S).

I4. Napravi stablo da bude više:

Ako je propagacija razdvajanja čvorova dovela do podele korena, napravi

novi koren čija su deca dva rezultujuća čvora.

Algoritam Izaberi_List(pravougaonik r, int h):

/* Vraća list na koji će smestiti novi pravougaonik r. */

C1. Inicijalizacija:

Postavi N da bude koren.

C2. Provera lista:

Ako je N koren, vrati N.

C3. Izaberi podstablo:

Ako je N nije list, izaberi ulaz (R, ptr, NHV)

sa minimalnom NHV vrednošću koja je veća od h.

C4. Spuštati se dok se ne dođe do lista:

Postavi N na čvor označen sa ptr i ponovi od C2.

Algoritam Podesi_stablo(skup S):

/* S je skup čvorova koji sadrži ažurirani čvor, njegove rođake (ako je došlo do prelivnanja) i najnoviji
napravljen čvor NN (ako je došlo do razdvajanja). Rutina se penje od nivoa lista prema korenu, podešavajući MGP and NHV čvorova koji pokrivaju čvorove u S. Propagira razdvajanje (ako postoji) */

A1. Ako se dosegne nivo korena, stani.

A2. Propagiran čvor se deli naviše:

Neka Np bude roditelj od N.

Ako je N bilo podeljeno neka NN bude novi čvor.

Ubaci NN u Np po tačnom rasporedu prema Hilbertovoj

vrednosti ako ima prostora. Inače pozovi Rukovanje_prelivenim(Np , NN ).

Ako je Np podeljeno, neka PP postane novi čvor.

A3. Prilagodi MGP i NHV na nivou roditelja:

Neka P bude skup roditelja za čvorove u S.

Prilagodi odgovarajuće MGP i NHV čvorova u P.

A4. Pređi na sledeći nivo:

Neka S postane skup roditelja P, sa

NN = PP, ako je Np podeljeno.

ponovi od A1.

Brisanje

U Hilbertovom R-stablu, nema potrebe za ponovnim ubacivanjem čvorova siročadi kad god dođe do prelivanja čvora oca. Umesto toga, mogu se pozajmiti ključevi od čvorova sa istim ocem, ili se preliven čvor spaja sa čvorovima sa kojima deli oca. Ovo je moguće jer čvorovi imaju jasan poredak (prema najvećoj Hilbertovoj vrednost); nasuprot tome, u R-stablima ne postoji takav koncept za čvorove sa istim ocem. Primetimo da operacije brisanja zahtevaju s sarađujućih čvorova sa istim ocem, do operacije ubacivanja zahtevaju s-1 čvor sa istim ocem. Algoritam Obriši(r): D1. Naći čvor domaćina: Izvršiti pretragu da bi se našao list koji sadrži r. D2. Izbrisati r: Ukloniti r iz čvora L. D3. Ako L preliva Pozajmiti neke sadržaje iz s sarađujućih čvorova sa istim ocem Ako su svi čvorovi sa istim ocem spremni da prelivaju spojiti s+1 čvor podesiti rezultujuće čvorove. D3. Podesiti MGP i NHV u roditeljskim nivoima Napraviti skup S koji sadrži čvor L i njegove sarađujuće čvorove sa istim ocem (ako je došlo do prelivanja). Pozvati Prilagodi_stablo(S).

Rukovanje prelivenim

Algoritam za rukovanje prelivenim u Hilbertovom R-stablu tretira prelivene čvorove ili prenošenjem nekih sadržaja u jedno od s-1 sarađujućih čvorova sa istim ocem, ili deleći s čvorova u s+1 čvor. Algorithm Rukovanje_prelivenim(čvor N, pravougaonik r):
/* vrati novi čvor ako je došlo do podele */ H1. Neka je ε skup koji sadrži sve sadržaje iz čvora N I njegovih s-1 sarađujućih čvorova sa istim ocem. H2. Dodati r u ε. H3. Ako bar jedan od s-1 sarađujućih čvorova sa istim ocem nije pun, rasporediti ε jednako među s čvorova prema Hilbert vrednostima.

H4. Ako su svih s sarađujućih čvorova sa istim ocem puni: Napraviti novi čvor NN I rasporediti ε jednako među s+1 čvorova prema Hilbert vrednostima Vratiti NN.

Референце

1. I. Kamel and C. Faloutsos, On Packing R-trees, Second International ACM Conference on Information and Knowledge Management (CIKM), pages 490-499, Washington D.C., 1993.
2. H. Jagadish. Linearno grupisanje objekata sa više atributa. U Proc. od ACM SIGMOD Conf., strane 332-342, Atlantic City, NJ, Maj 1990.
3. J. Griffiths. An algorithm for displaying a class of space-filling curves, Software-Practice and Experience. . 16 (5): 403—411.  Недостаје или је празан параметар |title= (помоћ), May 1986.
4. T. Bially. Space-filling curves. Their generation and their application to bandwidth reduction. IEEE Trans. on Information Theory. IT . 15 (6): 658—664.  Недостаје или је празан параметар |title= (помоћ), November 1969.
5. Beckmann, Norbert; Kriegel, Hans-Peter; Schneider, Ralf; Seeger, Bernhard (1990). „The R*-tree: An efficient and robust access method for points and rectangles”. Proceedings of the 1990 ACM SIGMOD international conference on Management of data. стр. 322–331. ISBN 0897913655. S2CID 11567855. doi:10.1145/93597.98741. 

Reference

• I. Kamel and C. Faloutsos. Parallel R-Trees. In Proc. of ACM SIGMOD Conf., pages 195-204 San Diego, CA, June 1992. Also available as Tech. Report UMIACS TR 92-1, CS-TR-2820.
• I. Kamel and C. Faloutsos. Hilbert R-tree: An improved R-tree using fractals. In Proc. of VLDB Conf., pages 500-509, Santiago, Chile, September 1994. Also available as Tech_ Report UMIACS TR 93-12.1 CS-TR-3032.1.
• N. Koudas, C. Faloutsos and I. Kamel. Declustering Spatial Databases on a Multi-Computer Architecture, International Conference on Extending Database Technology (EDBT), pages 592-614, 1996.
• N. Roussopoulos and D. Leifker. Direct spatial search on pictorial databases using Packed R-trees. In Proc. of ACM SIGMOD, pages 17-31, Austin, TX, May 1985.
• M. Schroeder. Fractals, Chaos, Power Laws: Minutes From an Infinite Paradise. W.H. Freeman and Company, NY, 1991.
• T. Sellis, N. Roussopoulos, and C. Faloutsos. The R+-Tree: a dynamic index for multi-dimensional objects. In Proc. 13th International Conference on VLDB, pages 507-518, England, September 1987.

Шаблон:CS stabla Шаблон:Strukture podataka